数据结构——平衡二叉搜索树(AvlTree)的实现
平衡二叉搜索树是二叉搜索树的升级版本。它拥有二叉搜索树的所有特性,同时它对子树的高度也进行了一定的限制。所以平衡二叉搜索树不会退化成链表的形式,而是维持了一个比较平衡的二叉树状态。
特点
在二叉搜索树的特点的基础上,平衡二叉树还要求对于任意节点X,X的左、右子树的深度相差最大不能超过1。如果某种操作(一般是插入和删除操作)破坏了这种平衡性,就要对树中不平衡的结点进行“旋转”来修复平衡性。
AvlTree
本平衡二叉搜索树的实现和之前的二叉搜索树实现很类似,都是包含了自定义的比较器。它们实现的不同点主要体现在平衡二叉搜索树的插入和删除操作要相对复杂一点,因为在元素插入或删除后,如果树的平衡性被破坏了还要进行平衡性的修复。
因为实现中需要频繁的计算左子树和右子树的高度差,所以我们在树中的节点里维护了一个表示当前结点的高度的变量。
成员变量
private AvlNode root : 平衡二叉搜索树。
private Comparator cmp : 比较器。
构造器
public AvlTree(){
this(null);
}
public AvlTree(Comparator<T> cmp){
this.root = null;
this.cmp = cmp;
}
函数
- isEmpty() :判断树是否为空树
- clearTree() :重置树为空树
- findMin() :查询树中最小值,还包含一个重载的内部方法的实现。
- findMax() :查询树中最大值,还包含一个重载的内部方法的实现。
- print() : 前序遍历的按递增顺序输出树的元素。
- innerComparaTo() :内部比较器实现。
contains() :二分查找查询树中是否包含元素X。
以上这些方法都是和二叉搜索树的类似或完全相同的,可以参考那边的实现,这里不再赘述了。传送门 ——> 二叉搜索树的实现
因为节点中维护了保存节点高度的变量,所以只要直接返回根节点的高度即可。
public int treeHeight(){
return root.height;
}
前序遍历方法检验是否为平衡二叉搜索树。
public boolean isAvlTree(){
return isAvlTree(root);
}
private boolean isAvlTree(AvlNode<T> tree){
/* 到叶子节点 */
if(tree == null)
return true;
int x = height(tree.right) - height(tree.left);
if(Math.abs(x) >= 2){
return false;
}
return isAvlTree(tree.left) && isAvlTree(tree.right);
}
insert():插入元素,主要在内部方法中递归实现。
插入元素后,要判断左子树和右子树的高度差是否符合要求(不大于1),否则就要进行旋转操作。
并且只有x位置到根节点的路径上涉及的节点可能会被改变。(x为插入元素的位置)
其中插入导致不平衡的情况只要有四种:(假设Q是需要重新平衡的节点)
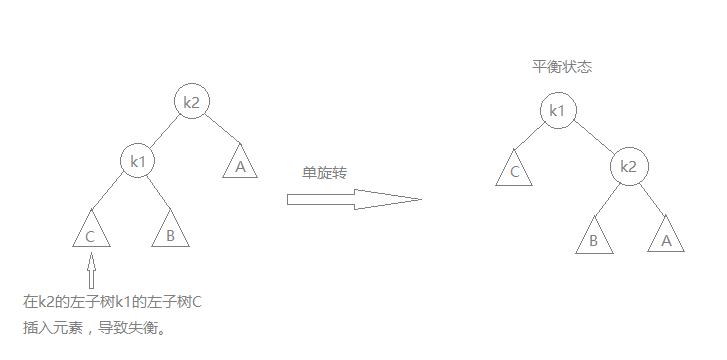
1.在Q左儿子的左子树插入元素;
2.在Q左儿子的右子树插入元素;
3.在Q右儿子的左子树插入元素;
4.在Q右儿子的右子树插入元素.
其中1,4是对称的情况,只需要单旋转就可以处理;
2,3是对称的情况,需要双旋转来处理.
public void insert(T x){
root = insert(x, root);
}
private AvlNode<T> insert(T x, AvlNode<T> tree){
if(tree == null)
return new AvlNode<T>(x);
int result = innerComparaTo(x, tree.element);
/* 在左子树中插入 */
if(result < 0){
tree.left = insert(x, tree.left);
/* 因为上一步在左子树加入新的元素,所以可能发生高度变化的是左子树.
* 所以当左子树高度与右子树高度相差2时则本节点发生了不平衡的情况
*/
if(height(tree.left) - height(tree.right) == 2){
/* 情况1 单旋转*/
if(innerComparaTo(x, tree.left.element) < 0)
tree = rotateWithLeftChild(tree);
/* 情况2 双旋转*/
else
tree = doubleRotateWithLeftChild(tree);
}
}
/* 在右子树中插入 */
else if(result > 0){
tree.right = insert(x, tree.right);
/* 同上分析 */
if(height(tree.right) - height(tree.left) == 2){
/* 情况4 单旋转*/
if(innerComparaTo(x, tree.right.element) > 0)
tree = rotateWithRightChild(tree);
/* 情况3 双旋转*/
else
tree = doubleRotateWithRightChild(tree);
}
}
/* 有相同的元素 */
else{
//这里不做任何处理
}
/* 更新节点的高度 */
tree.height = Math.max(height(tree.left), height(tree.right)) + 1;
return tree;
}
这个算法不保证对的!
这个算法不保证对的!
这个算法不保证对的!
重要的事情说三遍,= =。因为是仿造insert方法蒙出来的。(说蒙出来是因为经过若干组测试发现结果好像是对的,所以才放上来。)
希望有大神帮看看本算法是不是可行,要是能指出错误并修正就更好了。= =。万分感谢。
public void remove(T x){
root = remove(x, root);
}
public AvlNode<T> remove(T x, AvlNode<T> tree){
/* 空树或没有找到要删除的元素 */
if(tree == null)
return null;
int result = innerComparaTo(x, tree.element);
/* 在左子树中删除元素 */
if(result < 0){
tree.left = remove(x, tree.left);
/* 判断是否左子树减少元素后导致了不平衡, 此时右子树高度至少为2 */
if(height(tree.right) - height(tree.left) == 2){
//System.out.println("左大:发生不平衡的节点:" + tree.element);
//print(root);
/* 如果右子树中的右子树高度比右子树中的左子树高度高,
可看做是右子树的右子树插入元素导致的不平衡 */
if(height(tree.right.right) >= height(tree.right.left))
tree = rotateWithRightChild(tree);
else
tree = doubleRotateWithRightChild(tree);
}
}
/* 在右子树中删除元素 */
else if(result > 0){
tree.right = remove(x, tree.right);
if(height(tree.left) - height(tree.right) == 2){
//System.out.println("右大:发生不平衡的节点:" + tree.element);
//print(root);
if(height(tree.left.left) >= height(tree.left.right))
tree = rotateWithLeftChild(tree);
else
tree = doubleRotateWithLeftChild(tree);
}
}
/* 找到要删除的元素,且该节点具有左子树和右子树 */
else if(tree.left != null && tree.right != null){
/* 找到右子树中最小节点,用其值替换本节点值,并删除右子树中值最小的节点 */
tree.element = findMin(tree.right);
tree.right = remove(tree.element, tree.right);
if(height(tree.left) - height(tree.right) == 2){
//System.out.println("右大:发生不平衡的节点:" + tree.element);
//print(root);
if(height(tree.left.left) >= height(tree.left.right))
tree = rotateWithLeftChild(tree);
else
tree = doubleRotateWithLeftChild(tree);
}
}
/* 找到要删除的元素,且该节点只有左子树或者右子树或左右子树都没有 */
else{
tree = tree.left != null ? tree.left : tree.right;
}
if(tree != null)
tree.height = Math.max(height(tree.left), height(tree.right)) + 1;
return tree;
}
单旋转
private AvlNode<T> rotateWithLeftChild(AvlNode<T> k2){
/* 旋转完k1上提,k2下沉 */
AvlNode<T> k1 = k2.left;
k2.left = k1.right;
k1.right = k2;
/* 更新节点的高度 */
k2.height = Math.max(height(k2.left), height(k2.right)) + 1;
k1.height = Math.max(height(k1.left), k2.height) + 1;
return k1;
}
private AvlNode<T> rotateWithRightChild(AvlNode<T> k2){
/* 旋转完k1上提,k2下沉 */
AvlNode<T> k1 = k2.right;
k2.right = k1.left;
k1.left = k2;
/* 更新节点的高度 */
k2.height = Math.max(height(k2.left), height(k2.right)) + 1;
k1.height = Math.max(height(k1.left), k2.height) + 1;
return k1;
}
双旋转
private AvlNode<T> doubleRotateWithLeftChild(AvlNode<T> k3){
/* 第一次旋转 k3的左儿子 */
k3.left = rotateWithRightChild(k3.left);
/* 第二次旋转k3 */
return rotateWithLeftChild(k3);
}
private AvlNode<T> doubleRotateWithRightChild(AvlNode<T> k3){
/* 第一次旋转k3的右儿子 */
k3.right = rotateWithLeftChild(k3.right);
/* 第二次旋转k3 */
return rotateWithRightChild(k3);
}
内部类
private static class AvlNode<T> {
public T element;
public AvlNode<T> left;
public AvlNode<T> right;
public int height;
public AvlNode(T ele){
this(ele, null, null);
}
public AvlNode(T ele, AvlNode<T> left, AvlNode<T> right){
element = ele;
this.left = left;
this.right = right;
}
}
源代码
import java.util.Comparator;
/** * 平衡二叉搜索树:左右子树深度相差最大不能超过1 * @author Bingo * * @param <T> */
public class AvlTree<T> {
private AvlNode<T> root;
private Comparator<T> cmp;
public AvlTree(){
this(null);
}
public AvlTree(Comparator<T> cmp){
this.root = null;
this.cmp = cmp;
}
public boolean isEmpty(){
return root == null;
}
public void clearTree(){
root = null;
}
/* 同二叉查找树 */
public boolean contains(T x){
return false;
}
/* 同二叉查找树 */
public T findMin(){
if(isEmpty())
return null;
return findMin(root);
}
/* 同二叉查找树 */
public T findMax(){
if(isEmpty())
return null;
return findMax(root);
}
/** * 插入元素x * @param x */
public void insert(T x){
root = insert(x, root);
}
/** * 移除元素x * @param x */
public void remove(T x){
root = remove(x, root);
}
public int treeHeight(){
return root.height;
}
public void print(){
print(root);
}
public boolean isAvlTree(){
return isAvlTree(root);
}
/** * 内部插入方法 * 插入时通过旋转来修正树的平衡性,并且只有x位置到根节点的路径上涉及的节点可能会被改变 * 其中插入导致不平衡的情况只要有四种:(假设Q是需要重新平衡的节点) * 1.在Q左儿子的左子树插入元素; * 2.在Q左儿子的右子树插入元素; * 3.在Q右儿子的左子树插入元素; * 4.在Q右儿子的右子树插入元素. * 其中1,4是对称的情况,只需要单旋转就可以处理; * 2,3是对称的情况,需要双旋转来处理. * @param x * @param tree * @return */
private AvlNode<T> insert(T x, AvlNode<T> tree){
if(tree == null)
return new AvlNode<T>(x);
int result = innerComparaTo(x, tree.element);
/* 在左子树中插入 */
if(result < 0){
tree.left = insert(x, tree.left);
/* 因为上一步在左子树加入新的元素,所以可能发生高度变化的是左子树. * 所以当左子树高度与右子树高度相差2时则本节点发生了不平衡的情况 */
if(height(tree.left) - height(tree.right) == 2){
/* 情况1 */
if(innerComparaTo(x, tree.left.element) < 0)
tree = rotateWithLeftChild(tree);
/* 情况2 */
else
tree = doubleRotateWithLeftChild(tree);
}
}
/* 在右子树中插入 */
else if(result > 0){
tree.right = insert(x, tree.right);
/* 同上分析 */
if(height(tree.right) - height(tree.left) == 2){
/* 情况4 */
if(innerComparaTo(x, tree.right.element) > 0)
tree = rotateWithRightChild(tree);
/* 情况3 */
else
tree = doubleRotateWithRightChild(tree);
}
}
/* 有相同的元素 */
else{
//这里不做任何处理
}
/* 更新节点的高度 */
tree.height = Math.max(height(tree.left), height(tree.right)) + 1;
return tree;
}
/** * 移除元素x (!!!不知道对不对,有待考证) * 可以近似的看作是插入操作的逆操作,导致不平衡的情况和插入操作一样有类似的四个原因。 * @param x * @param tree */
public AvlNode<T> remove(T x, AvlNode<T> tree){
/* 空树或没有找到要删除的元素 */
if(tree == null)
return null;
int result = innerComparaTo(x, tree.element);
/* 在左子树中删除元素 */
if(result < 0){
tree.left = remove(x, tree.left);
/* 判断是否左子树减少元素后导致了不平衡, 此时右子树高度至少为2 */
if(height(tree.right) - height(tree.left) == 2){
//System.out.println("左大:发生不平衡的节点:" + tree.element);
//print(root);
/* 如果右子树中的右子树高度比右子树中的左子树高度高,可看做是右子树的右子树插入元素导致的不平衡 */
if(height(tree.right.right) >= height(tree.right.left))
tree = rotateWithRightChild(tree);
else
tree = doubleRotateWithRightChild(tree);
}
}
/* 在右子树中删除元素 */
else if(result > 0){
tree.right = remove(x, tree.right);
if(height(tree.left) - height(tree.right) == 2){
//System.out.println("右大:发生不平衡的节点:" + tree.element);
//print(root);
if(height(tree.left.left) >= height(tree.left.right))
tree = rotateWithLeftChild(tree);
else
tree = doubleRotateWithLeftChild(tree);
}
}
/* 找到要删除的元素,且该节点具有左子树和右子树 */
else if(tree.left != null && tree.right != null){
/* 找到右子树中最小节点,用其值替换本节点值,并删除右子树中值最小的节点 */
tree.element = findMin(tree.right);
tree.right = remove(tree.element, tree.right);
if(height(tree.left) - height(tree.right) == 2){
//System.out.println("右大:发生不平衡的节点:" + tree.element);
//print(root);
if(height(tree.left.left) >= height(tree.left.right))
tree = rotateWithLeftChild(tree);
else
tree = doubleRotateWithLeftChild(tree);
}
}
/* 找到要删除的元素,且该节点只有左子树或者右子树或左右子树都没有 */
else{
tree = tree.left != null ? tree.left : tree.right;
}
if(tree != null)
tree.height = Math.max(height(tree.left), height(tree.right)) + 1;
return tree;
}
/** * 获取节点x的高度 * @param x * @return 如果x为null,则返回-1,否则返回节点高度 */
private int height(AvlNode<T> x){
return x == null ? -1 : x.height;
}
/** * 单旋转左子树 * @param tree * @return */
private AvlNode<T> rotateWithLeftChild(AvlNode<T> k2){
/* 旋转完k1上提,k2下沉 */
AvlNode<T> k1 = k2.left;
k2.left = k1.right;
k1.right = k2;
/* 更新节点的高度 */
k2.height = Math.max(height(k2.left), height(k2.right)) + 1;
k1.height = Math.max(height(k1.left), k2.height) + 1;
return k1;
}
/** * 双旋转左子树 * @param tree * @return */
private AvlNode<T> doubleRotateWithLeftChild(AvlNode<T> k3){
/* 第一次旋转 k3的左儿子 */
k3.left = rotateWithRightChild(k3.left);
/* 第二次旋转k3 */
return rotateWithLeftChild(k3);
}
/** * 单旋转右子树 * @param tree * @return */
private AvlNode<T> rotateWithRightChild(AvlNode<T> k2){
/* 旋转完k1上提,k2下沉 */
AvlNode<T> k1 = k2.right;
k2.right = k1.left;
k1.left = k2;
/* 更新节点的高度 */
k2.height = Math.max(height(k2.left), height(k2.right)) + 1;
k1.height = Math.max(height(k1.left), k2.height) + 1;
return k1;
}
/** * 双旋转右子树 * @param tree * @return */
private AvlNode<T> doubleRotateWithRightChild(AvlNode<T> k3){
/* 第一次旋转k3的右儿子 */
k3.right = rotateWithLeftChild(k3.right);
/* 第二次旋转k3 */
return rotateWithRightChild(k3);
}
private T findMin(AvlNode<T> tree){
while(tree.left != null)
tree = tree.left;
return tree.element;
}
private T findMax(AvlNode<T> tree){
while(tree.right != null)
tree = tree.right;
return tree.element;
}
/** * 内部比较器 * @param lhs * @param rhs * @return */
@SuppressWarnings("unchecked")
private int innerComparaTo(T lhs, T rhs){
if(cmp != null)
return cmp.compare(lhs, rhs);
return ((Comparable<T>)lhs).compareTo(rhs);
}
private void print(AvlNode<T> tree){
if(tree == null)
return;
print(tree.left);
for(int i=0; i < tree.height; i++)
System.out.print("\t");
System.out.println("(" + tree.element + ")");
print(tree.right);
}
/** * 后序遍历来检验整棵树是不是平衡二叉树 * @param tree * @return */
private boolean isAvlTree(AvlNode<T> tree){
/* 到叶子节点 */
if(tree == null)
return true;
int x = height(tree.right) - height(tree.left);
if(Math.abs(x) >= 2){
return false;
}
return isAvlTree(tree.left) && isAvlTree(tree.right);
}
/** * 私有类,平衡二叉树的节点类。 * 除了常规的元素值,左右子节点的引用外,还维护了节点的高度 * @author Bingo * * @param <T> */
private static class AvlNode<T> {
public T element;
public AvlNode<T> left;
public AvlNode<T> right;
public int height;
public AvlNode(T ele){
this(ele, null, null);
}
public AvlNode(T ele, AvlNode<T> left, AvlNode<T> right){
element = ele;
this.left = left;
this.right = right;
}
}
}测试代码
这里的测试主要是测试insert和remove方法执行之后,树是否还是平衡二叉树。
import org.junit.Test;
import com.lysongzi.collection.AvlTree;
import com.lysongzi.util.RandomNumberGenerator;
import junit.framework.Assert;
public class AvlTreeTest {
private AvlTree<Integer> at;
private static final int size = 10000;
private static final int up = size * 10;
private static final int down = 0;
@SuppressWarnings("deprecation")
@Test
public void test() {
at = new AvlTree<Integer>();
/* 自己写的一个方法返回一个Integer数组而已 */
Integer[] ia = RandomNumberGenerator.getIntegreArrayWithBound(size, down, up);
for(int i=0; i < ia.length; i++){
at.insert(ia[i]);
//Assert.assertEquals(at.isAvlTree(), true);
}
System.out.println("insert finish. tree height = " + at.treeHeight());
for(int i=0; i < ia.length; i++){
System.out.println("正在删除的值ia["+i+"] = " + ia[i]);
//at.print();
at.remove(ia[i]);
Assert.assertEquals(at.isAvlTree(), true);
}
System.out.println("remove finish.");
}
}
参考资料
- 《数据结构与算法分析-java语言描述 第2版》Mark Allen Weiss. 机械工业出版社.