C语言 一元二次方程求根的拓展

一元二次方程求根的拓展

       对于一元二次方程大家都不会陌生吧，这是一个从小学就开始学习和了解的知识点了，

对于这个求根方程要分为很多的情况，但是我们都知道，当   b^2-4ac小余0是方程是没有解

的，但是随着知识面的扩展，这种情况也是可以有解，不过不是实数，而是复数

下面就让我来为你实现这段代码吧

当 

tem=b^2-4ac<0

时

对它开平方根可以得到   为sqrt(tem)*i;因为大家都知道 i*i=-1  

所以

下面就是

temp=-b/(2*a);

则可以得到  

两个解为   x1=temp+sqrt(tem)*i/(2*a)

                  x2=temp-sqrt(tem)*i/(2*a)

代码分析

</pre><pre name="code" class="html">

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<stdlib.h>
//写程序求一元二次方程的解。
#define exp  0.00001
void function(double a,double b,double c)
{
	double tem=0,temp=0;
	if((a>(-exp))&&(a<exp))//  a=0时为一元一次方程
	{
	printf("此方称的解为：%.2f \n",-c/b);
	}
	else
	{
	    tem=b*b-4*a*c;
		temp=-b/(2*a);
		if(tem>0)//     b*b-4ac   >0

		{
			printf("此方程的两个解为：%.2f, %.2f\n",temp+sqrt(tem)/(2*a),temp-sqrt(tem)/(2*a));
		}
		else if((tem>(-exp))&&(tem<exp)) //   b*b-4ac   ==0
		{
			printf("此方程的解为： %.2f\n",temp);
		}
		else //     b*b-4ac   <0 
		{
			tem=-tem;
			printf("此方程的的两个解为：%.2f + %.2fi  ,  %.2f - %.2fi",temp,sqrt(tem)/(2*a),temp,sqrt(tem)/(2*a));

		}

	}
}
int main()
{
	double a[3]={0};
	int i=0;
	printf("请输入一元二次方程的三个参数：");
	for(i=0;i<3;i++)
    {
		  scanf("%lf",&a[i]);
	}
	function(a[0],a[1],a[2]);

	system("pause");
	return 0;

}

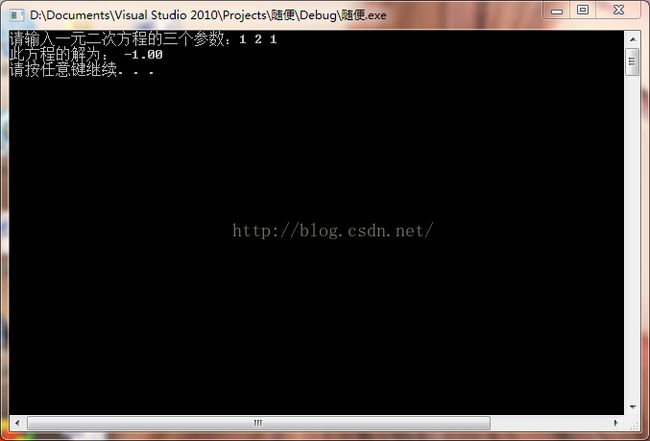
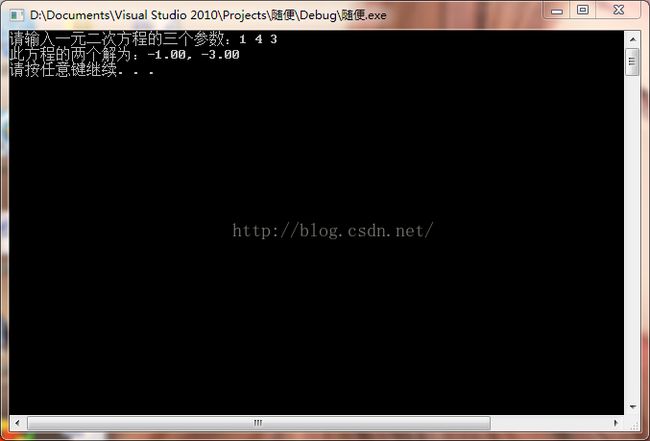
三种输出结果：

这个就是本片的重点输出，两个解为复数

这个shi  b*b-4ac等于0时的输出，方程只有一个解

这个shi  b*b-4ac大于0时的输出，方程只有二个解

今天只有这 么简单一个程序，最近都太忙了，没有时间写博客了，不知什么时候这些个日子才是个头