graph-cut

【简介】

Graph Cuts 不等于 graph cut(如 min cut、normalized cut、RatioCut)， 是最近在计算机视觉中研究和应用比较多的energy minimization（能量函数最小化）优化算法，典型的用于stereo matching, image restortion, texture synthesis等应用。

 

这个优化算法用来解 markov Random Field. 有实验<Comparison of Graph Cuts with Belief Propagation for Stereo, using Identical MRF Parameters>显示，Graph Cuts比用Belief Propagation更好，比用dynamic programming(只用1D求解), gradient decedent, simulated annealing, etc 要好得更多；特别是使用a-b-swap, 和 a-expansion的时候。

 

【原理】

• <Fast Approximate Energy Minimization via Graph Cuts> (Boykov, Veksler and Zabih, PAMI '01)，这篇paper是graph cuts的开山之作，系统介绍了如何构造graph和energy term来解stereo disparity, motion等问题，也比较直观的介绍了a-expansion。

 

• <GRAPH BASED ALGORITHMS FOR SCENE RECONSTRUCTION FROM TWO OR MORE VIEWS> (Kolmogorov's PhD thesis 04), 这篇论文是Kolmogorov的博士论文，实现了Graph CUT用于立体视觉的匹配，它改善了传统GRAPH CUT计算耗时的缺点，他还因此称为微软一员，专门从事GRAPH CUT在图像处理上的应用。

 

• <What energy functions can be minimized via graph cuts> (Kolmogorov PAMI '04). 本文首先介绍了需要通过graph cut最小化的能量函数的特性。虽然是二进制变量但是很容易推广到其他方面。详细描述了通过graphcut最小化的能量函数。并提供了最小化能量函数的通用构建。最后给出了最小化二进制能量函数的必要条件。

 

• <Interactive Graph Cuts for Optimal Boundary & Region Segmentation of Objects in N-D Images> (Boykov iccv01) 这篇paper讲怎么用graphcut来做image segmentation。

 

 【应用】

Graph cuts最主要的应用是图像分割。

在Boykov 和 Kolmogorov 俩人的主页上就有大量的code。包括maxflow/min-cut、stereo algorithms等算法：

http://vision.csd.uwo.ca/code/

http://www.cs.ucl.ac.uk/staff/V.Kolmogorov/software.html

 

以及olga. Veksler的

http://www.csd.uwo.ca/faculty/olga/code.html

 

[转] http://blog.sina.com.cn/s/blog_48e673350100wan9.html

 

 

---------------------------------------------------------------------------

 

 

Graph cut是一种energy minimization的方法，用来解first-order markov Random Field比用Belief Propagation感觉更好，比用dynamic programming(只用1D求解), gradient decedent, simulated annealing, etc 要好得更多；特别是使用a-b-swap, 和 a-expansion的时候。刚开始看graph cut的时候不着门道，走了很多弯路，现在总结起来可以这样学习：

1。学习algorithm课本里的关于graph那一节，或者google maxflow/mincut相关的内容，有介绍mincut的两种解法；

2。然后就开始看用graphcut解决computer vision里的问题，首先要看的是《Interactive Graph Cuts for Optimal Boundary & Region Segmentation of Objects in N-D Images》iccv 01。这篇paper讲怎么用graphcut来做image segmentation；

3。看Fast Approximate Energy Minimization via Graph Cuts (Boykov, Veksler and Zabih, PAMI '01)，这篇paper系统介绍了如何构造graph和energy term来解stereo disparity, motion等问题，也比较直观的介绍了a-expansion。后面的关于graphcut的TPAMI的文章都没有介绍如何构造graph来解问题， 这篇比较关键；

看了以上几个文章后，基本就可以看懂关于graphcut的论文了，就可以深入下去了。

http://www.cs.cornell.edu/~rdz/graphcuts.html

 

[转]http://apps.hi.baidu.com/share/detail/22906202

______________________________________________________________________________________________________

Graphcut,让人欢喜让人忧

2007-09-06 21:50

终于和陈贤弟，进入Graphcut得学习了，只是这一块一直为我所难以啃掉得硬骨头，在我毕业之前能不能咬下来，希望可以，只是近日再度回首，发现其涉及得理论，有一点前沿，虽然三四年前提出得东西，但由于作者交代得简单，含糊，使得这一技术得应用受到了严重得限制，几乎很多人都知道 Graphcut可是又有多少人可以实现这个Graphcut呢，寥寥无几吧，一年前我不懂，一年后得今天，还在为这个而愁眉不展，不忘早点解决这个问题，当然，还得于陈贤弟好好交流合作了。 Graphcut是一座大山，可是翻过了这座大山，后面还有一座更大得，不过更激发我兴趣得大山要去翻越。真实永无止境啊！ 上次××问我Graphcut怎么实现 我不知道，估计他也不一定懂，过段时间我实现了，就可以比上次有更大得进步了。自信也会提高很多得

 

Graph cut

Graph cut是一种energy minimization的方法，用来解first-order markov Random Field比用Belief Propagation感觉更好，比用dynamic programming(只用1D求解), gradient decedent, simulated annealing, etc 要好得更多；特别是使用a-b-swap, 和 a-expansion的时候。刚开始看graph cut的时候不着门道，走了很多弯路，现在总结起来可以这样学习：

1。学习algorithm课本里的关于graph那一节，或者google maxflow/mincut相关的内容，有介绍mincut的两种解法；
2。然后就开始看用graphcut解决computer vision里的问题，首先要看的是《Interactive Graph Cuts for Optimal Boundary & Region Segmentation of Objects in N-D Images》iccv 01。这篇paper讲怎么用graphcut来做image segmentation；
3。看 Fast Approximate Energy Minimization via Graph Cuts (Boykov, Veksler and Zabih, PAMI '01)，这篇paper系统介绍了如何构造graph和energy term来解stereo disparity, motion等问题，也比较直观的介绍了a-expansion。后面的关于graphcut的TPAMI的文章都没有介绍如何构造graph来解问题，这篇比较关键；

看了以上几个文章后，基本就可以看懂关于graphcut的论文了，就可以深入下去了。

http://www.cs.cornell.edu/~rdz/graphcuts.html

 

关于Graph cuts的简介及相关资源

【简介】

Graph Cuts 不等于 graph cut(如 min cut、normalized cut、RatioCut)， 是最近在计算机视觉中研究和应用比较多的energy minimization（能量函数最小化）优化算法，典型的用于stereo matching, image restortion, texture synthesis等应用。

这个优化算法用来解 markov Random Field. 有实验<Comparison of Graph Cuts with Belief Propagation for Stereo, using Identical MRF Parameters> 显示，Graph Cuts比用Belief Propagation更好，比用dynamic programming(只用1D求解), gradient decedent, simulated annealing, etc 要好得更多；特别是使用a-b-swap, 和 a-expansion的时候。

【原理】

<Fast Approximate Energy Minimization via Graph Cuts>  ( Boykov, Veksler and Zabih, PAMI '01)，这篇paper是graph cuts的开山之作，系统介绍了如何构造graph和energy term来解stereo disparity, motion等问题，也比较直观的介绍了a-expansion。 <GRAPH BASED ALGORITHMS FOR SCENE RECONSTRUCTION FROM TWO OR MORE VIEWS>  (Kolmogorov's PhD thesis 04), 这篇论文是 Kolmogorov的博士论文，实现了Graph  CUT用于立体视觉的匹配，它改善了传统GRAPH CUT计算耗时的缺点，他还因此称为微软一员，专门从事GRAPH CUT在图像处理上的应用。 <What energy functions can be minimized via graph cuts>  (Kolmogorov PAMI '04).  本文首先介绍了需要通过graph cut最小化的能量函数的特性。虽然是二进制变量但是很容易推广到其他方面。详细描述了通过graphcut最小化的能量函数。并提供了最小化能量函数的通用构建。最后给出了最小化二进制能量函数的必要条件。 < Interactive Graph Cuts for Optimal Boundary & Region Segmentation of Objects in N-D Images >  ( Boykov  iccv01)  这篇paper讲怎么用graphcut来做image segmentation。

【应用】

Graph cuts最主要的应用是图像分割。

在Boykov 和 Kolmogorov 俩人的主页上就有大量的code。包括maxflow/min-cut、stereo algorithms等算法：

http://vision.csd.uwo.ca/code/

http://www.cs.ucl.ac.uk/staff/V.Kolmogorov/software.html

以及olga. Veksler的

http://www.csd.uwo.ca/faculty/olga/code.html

【toolkit】

Lazy SnappingGrabCut

Trackback: http://blog.csdn.net/hebby06/archive/2010/03/03/5341228.aspx

[论文笔记] CUDA Cuts: Fast Graph Cuts on the GPU    http://lincccc.blogbus.com/logs/107588061.html

____________________________________________________________________________________________________

网络流算法最初用于解决流网络的优化问题，比如水管网络、通信传输和城市的车流等。Graph cut作为其中一类最常见的算法，用于求解流网络的最小割，即寻找一个总容量最小的边集合，去掉这个集合中的所有边将阻断这个网络。图像和视频也能被视作网络（或者MRF），以像素作为节点，具体应用定义相邻像素间边的能量值（容量）。因此从九十年代末开始，Graph cut渐渐被引入计算机视觉、图像处理和机器学习领域，用于优化分类、分割和合成等问题。

The Max-Flow and Min-Cost Problem： 
定义图（或者流网络）G = (V, E)，可以为有向图或无向图。图中所有的边 e(u, v) ∈ E 附有一个非负的容量 c(u, v) ≥ 0，即该边所能承受的最大流量。图中通常定义两个特殊的节点，源点 s 和终点 t；存在拥有多个端点的图，对其的Max-flow求解为NP问题，需要转化为双端点问题求解次优解。定义满足以下条件的 f : VXV → R 为图 G 上的流：
   ●  Capacity Constrain，对于所有 u, v ∈ V，f(u, v) ≤ c(u, v)
   ●  Skew Symmetry，对于所有 u, v ∈ V，f(u, v) = ﹣f(u, v)
   ●  Flow Conservation，对于所有 u ∈ V﹣{s, t} 和 v ∈ V，∑ f(u, v) = 0
从 s 出发的所有流量的总和就是整个图的总流量。如下图所示，图的当前总流量为19，没有达到最大值。

 
Cut（割）将整个图的所有节点分为两个不相交的集合  S 和  T，比如 s ∈ S， t ∈ T。割的容量定义为：
      c(S, T) = ∑_x∈S ∑_y∈T c(x, y)。
Min-cut（最小割）就是图的所有割中容量最小的一个。算法上要直接找Min-cut是十分困难的，根据最大流最小割定理，即图的最大流量等于图的最小割容量，通常要将问题转化为与之等价的Max-flow问题（理论推导 点我）。

Max-Flow and Min-Cost Algorithms：
Max-flow问题的求解有两类经典的算法，增广路径[1] 和Push-relabel [2]。增广路径类算法遵循循序渐进的原则，不断在图上查找从 s 到 t 的可用路径，从0开始慢慢地提升图的总流量至最大；而Push-relabel类算法则从局部出发，总是尽可能地向图中输送更多的流量，在不断重复的Push和Relabel操作中达到节点间的平衡，是水流的一种拟态。Push-relabel类算法具有较高的并行性，适用于GPU加速，大体流程点我。
增广路径类算法有很多衍生，但大多具有以下特性：1）维护残余容量网络；2）通过寻找Augmenting path逼近最大流。Augmenting path具有形式：s, e1, v1, e2, v2, … , ek, t，其中没有重复的节点、没有饱和的前向边和空流量的后向边。对残余网络的定义有很多形式，这里我们定义边的残余容量（Redsidual capacity，RC）当其为前向边时等于 c(i, j) – f(i, j)，当其为后向边时等于 f(i, j)，如下图所示。

 
Augmenting path的残余容量为其每条边残余容量的最小值，如上图路径的残余容量为1。Ford-Fulkerson算法不断在残余网络中查询Augmenting path，比如使用广度或深度优先搜索，直到再也找不到任何路径。例子 点我。Boykov[3] 提出一种双向搜索并重用搜索树的增广路径算法，虽然理论复杂度较高，但在实际应用中却效率较高，因此很多需要Graph cut的应用都采用Boykov提供的源代码。

Applications in Computer Vision：
计算机视觉中很多问题，都可以归结为量化方程的优化问题。比如图像分割的问题，定义每一个像素属于前景或背景的可能性度量，那整个问题就变成了如何让整个可能性量化方程取值最大的问题。当然有时，我们还需要定义平滑项，用于约束相邻像素的属性变化。这就形成了在视觉中最为常见的一类能量优化方程：
      E(f) = Esmooth(f) + Edata(f)
1维图还可用动态规划方法求解，但2维以上由于其几何级的复杂度增长，则大多使用Graph cut。典型的应用有Segmentation、Stereo matching、Image Restoration、Motion estimation等。根据不同的应用有不同的图构、相邻约束和能量函数。Kolmogorov[4] 研究了什么样的能量方程能用Graph cut优化，并提出了三元及以下能量函数自动转换成图的方法。

Multi-label Graph Cut：
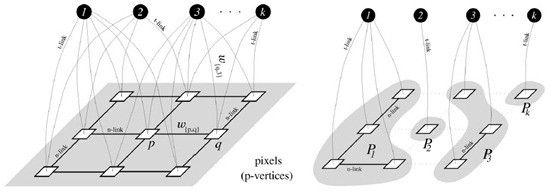
根据应用的需要，有时定义的图构是多个label的，也就是有多个灭点，如下图所示。这种图的Min-cut是Multi-way的，求解过程是一个NP问题（Boykov[3]在他的论文中有详细证明）。比如Stereo matching中的disparity、Image Restoration中的intensity等，其本质都是一个Multi-label的优化问题。虽然有些方法可以将其人为地转变为2-label，但这在很大程度上限制了能量函数的定义。

 

Boykov[3]提出了两种算法，能够在多项式时间内逼近Muli-label问题的最优解，并给出了详细证明和两种算法的optimality property讨论。这是一篇值得细读的文章。这两种方法都是在寻找Local minima，最终使得图中的任意一个像素改变其label都不能产生更好的解。在每一次迭代中，两种方法分别进行   α-expansion  和   α-β-swap   形式的move 优化。 α-expansion move  是指扩展   α-label   区域，使原本其他 label 的点属于   α ； α-β-swap move  则只针对   α-label   和   β-label   区域，使其中的一些点的label从   α  变为   β   或相反 。 每一部迭代都是一次2-label的优化过程，形成以   α  和   非α  为灭点、以及以   α  和   β   为灭点的图，寻找最优cut，重整label，不断逼近最优解。 α-expansion   要求平滑项满足三边定理，而   α-β-swap 可用于任意平滑项定义；但   α-expansion   有严格的optimality property bound，总不会产生太坏的结果，因此被较多地使用。

Dynamic Graph Cut：
动态图指一个图序列，在时序上前后图直接会保持平滑的过渡，因此，是否可以在前一张图的residual graph基础上修改变化了的像素点的能量以快速地求解？Dynamic graph cut并不寻求最优解，而是次优的快速的解。Kohli[12] 使用重新参数化图（Graph Reparameterization）的方法修改动态变化的数值，并保持Capacity、Flow等基本约束，而后直接得到次优解。这种方法可以容忍少量边的修改和少量任意节点拓扑的重构，但是和其他所有Dynamic graph cut算法一样，以少量、也就是轻微的时序变化为前提。主要应用于视频相关的视觉方法，如Video segmentation。

 

Bibliography：
[1] L. Ford , D. Fulkerson. Flows in Networks. Princeton University Press, 1962.
[2] Andrew V. Goldberg, Robert E. Tarjan. A new approach to the maximum-flow problem. In Journal of the Association for Computing Machinery, 35(4):921–940, October 1988.
[3] Y. Boykov, V. Kolmogorov. An Experimental Comparison of Min-Cut/Max-Flow Algorithms for Energy Minimization in Vision. In IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), volume 26, page 1124-1137, 2004.
[4] V. Kolmogorov, R. Zabih. What Energy Functions Can Be Minimized via Graph Cuts? In IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), volume 26, no.2, page 147-159, 2004.
[5] V. Kolmogorov, R. Zabih. Multi-camera Scene Reconstruction via Graph Cuts. In European Conference on Computer Vision (ECCV), May 2002 (best paper).
[6] Y. Boykov, O. Veksler and R. Zabih. Faster approximate energy minimization via graph cuts. In IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), volume 23, no. 11, page 1-18, 2001.
[7] S. Roy, I. Cox. A maximum-flow formulation of the n-camera stereo correspondence problem. In International Conference on Computer Vision (ICCV), 1998.
[8] V. Vineet, P. J. Narayanan. CUDA Cuts: Fast Graph Cuts on the GPU. In: CVPR Workshop on Visual Computer Vision on GPUs, 2008.
[9] V. Kwatra, A. Schodl, I. Essa, G. Turk and A. Bobick. Graphcut Textures: Image and Video Synthesis Using Graph Cuts. In SIGGRAPH 2003, pp. 277-286.
[10] A. Blum, J. Lafferty, M.R. Rwebangira and R. Reddy. Semi-Supervised Learning Using Randomized Mincuts. In Proceedings of the 21st International Conference on Machine Learning (ICML), Banff, Canada 2004.
[11] S. Z. Li, Markov Random Field Modeling in Computer Vision, Springer Verlag, 1995.
[12] P. Kohli and P. H. S. Torr. Dynamic graph cuts for efficient inference in markov random fields. IEEE Trans. Pattern Anal. Mach. Intell. (PAMI), 29(12):2079–2088, 2007.

_____________________________________________________________________________________________________

【简介】

Graph Cuts 不等于 graph cut(如 min cut、normalizedcut、RatioCut)， 是最近在计算机视觉中研究和应用比较多的energyminimization（能量函数最小化）优化算法，典型的用于stereo matching, image restortion,texture synthesis等应用。

 

这个优化算法用来解 markov Random Field. 有实验<Comparisonof Graph Cuts with Belief Propagation for Stereo, usingIdentical MRFParameters>显示，Graph Cuts比用BeliefPropagation更好，比用dynamic programming(只用1D求解), gradient decedent,simulated annealing, etc 要好得更多；特别是使用a-b-swap, 和 a-expansion的时候。

 

【原理】

• <FastApproximate Energy Minimization via GraphCuts> (Boykov, Veksler and Zabih, PAMI'01)，这篇paper是graph cuts的开山之作，系统介绍了如何构造graph和energy term来解stereodisparity, motion等问题，也比较直观的介绍了a-expansion。

 

• <GRAPHBASED ALGORITHMS FOR SCENE RECONSTRUCTION FROM TWOOR MORE VIEWS> (Kolmogorov'sPhD thesis 04), 这篇论文是Kolmogorov的博士论文，实现了Graph CUT用于立体视觉的匹配，它改善了传统GRAPHCUT计算耗时的缺点，他还因此称为微软一员，专门从事GRAPH CUT在图像处理上的应用。

 

• <Whatenergy functions can be minimized via graphcuts> (Kolmogorov PAMI'04). 本文首先介绍了需要通过graphcut最小化的能量函数的特性。虽然是二进制变量但是很容易推广到其他方面。详细描述了通过graphcut最小化的能量函数。并提供了最小化能量函数的通用构建。最后给出了最小化二进制能量函数的必要条件。

 

• <InteractiveGraph Cuts for Optimal Boundary & RegionSegmentation of Objects in N-D Images> (Boykov iccv01) 这篇paper讲怎么用graphcut来做imagesegmentation。

 

 

【应用】

Graph cuts最主要的应用是图像分割。

在Boykov 和 Kolmogorov 俩人的主页上就有大量的code。包括maxflow/min-cut、stereoalgorithms等算法：

http://vision.csd.uwo.ca/code/

http://www.cs.ucl.ac.uk/staff/V.Kolmogorov/software.html

 

以及olga. Veksler的

http://www.csd.uwo.ca/faculty/olga/code.html

__________________________________________________________________________________________________