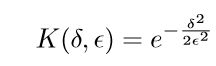Graph-Cut RANSAC(CVPR 2018)
基于图割优化的RANSAC算法
1. 摘要
本文提出了一种新的鲁棒估计算法,叫做图割RANSAC,简称GC-RANSAC。当找到当前最好模型时,该算法在局部优化中使用图割算法来区分内点和外点。本文提出的局部优化算法理论简洁、易于实现,是全局最优解且效率高。
基于仿真合成测试数据和真实图片对的实验表明,GG-RANSAC在一系列问题上(比如,直线拟合,单应矩阵、仿射矩阵、基本矩阵以及本质矩阵的估计)的结果比当前最好的算法更加精确。对于许多问题的求解,该算法能够以接近精确度小的算法的速度实时运行(在标准CPU上运行时间为毫秒级)。
2. 主要贡献
本文提出了一种使用局部优化算法改进RANSAC精度的方法,其主要贡献为:
(1)提出了一种考虑空间一致性的内点判断方法,从而改进了RANSAC算法的精度;
(2)采用图割算法解决内点判断的优化问题,提高了算法的效率。
3. 算法流程
传统的RANSAC算法主要包括如下步骤:
(1)随机采样计算模型需要的最少数据;
(2)由采样的数据计算出模型参数;
(3)计算其余数据对模型的匹配程度;
(4)重复1-3直到找到匹配程度最高的模型。
其中,第三步的判断方法一般为:分别判断每一个数据与模型的距离是否小于某一个阈值,满足则定义为内点,否则定义为外点。这样的判断准则比较生硬,且没有考虑数据的空间一致性。
本文的主要工作就是改进了第三步的准则。下面将进行具体的介绍:
A. 基于能量函数最小化的内点判断
当计算得到模型时,内点的判断可以看做一个最小化能量函数的问题,传统的RANSAC算法内点判断问题等价于:
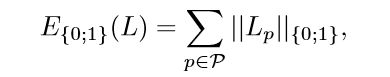
其中,
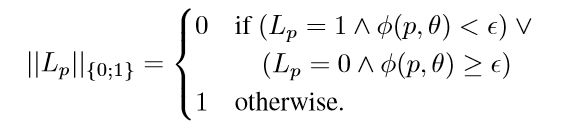
上式中, L p L_p Lp即为点的真实标签(内点为1,外点为0),也是需求取的变量。容易看出,上式的解即为:距离小于阈值的点为1,大于阈值的点为0——与传统的判别方法一致。 由于标签值只有0和1,因此比较生硬,无法更细致的刻画点和模型的匹配程度,因此往往引入核函数(如高斯函数),此时:
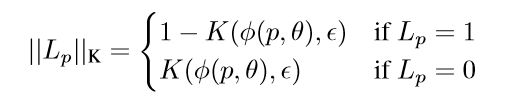
B. 空间一致性
空间一致性是指:在空间上相近的点,往往具有相同的标签(内点或外点)。本文将这一思想引入RANSAC中。考虑到可能出现外点多于内点的情况,提出了如下的准则:
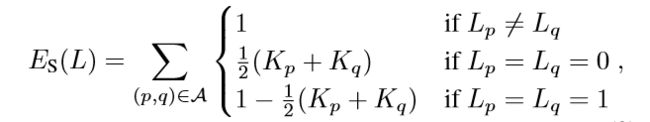
上式第一行表示:惩罚标签不一致的邻近点;第二行表示:如果两个点都为外点,则其与模型的接近程度越大,给予的惩罚越大;第三行表示:如果两个点都为内点,则其与模型越匹配,惩罚越小。
得到全局优化方程:
![]()
![]()
C. GC-RANSAC
整个GC-RANSAC算法如下:

其中为控制局部优化的次数,使得局部优化的效果尽可能发挥最大,本文提出了如下准则:仅当 μ 12 {\mu}_{12} μ12大于一定值时,才进行局部优化。
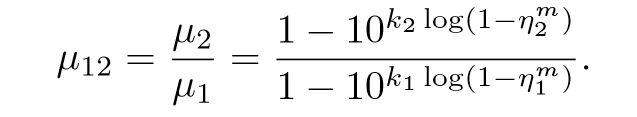
μ 1 {\mu}_{1} μ1, μ 2 {\mu}_{2} μ2表示对当前模型的置信度。
图模型的构建算法为:

由于待求解变量的取值为0和1,因此可以使用基于图割的算法进行快速的求解。
4. 主要结果
作者在仿真和真实数据上进行了实验,并与经典RANSAC, LO-RANSAC , LO±RANSAC, LO’-RANSAC, and EP-RANSAC等算法进行了对比,实验结果如下:
A. 2D线段检测仿真实验
该实验使用仿真合成的数据:在600x600的图像中,生成一条直线,并采样100个点,对采样点加入高斯白噪声。实验数据示意图如下:
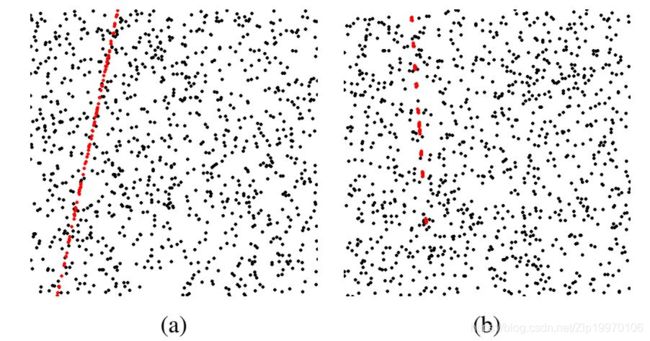
图1. 直线(a)和点画线(b)拟合算法结果示例。1000个黑色点是外点,100个红色点为内点。
实验结果如下:
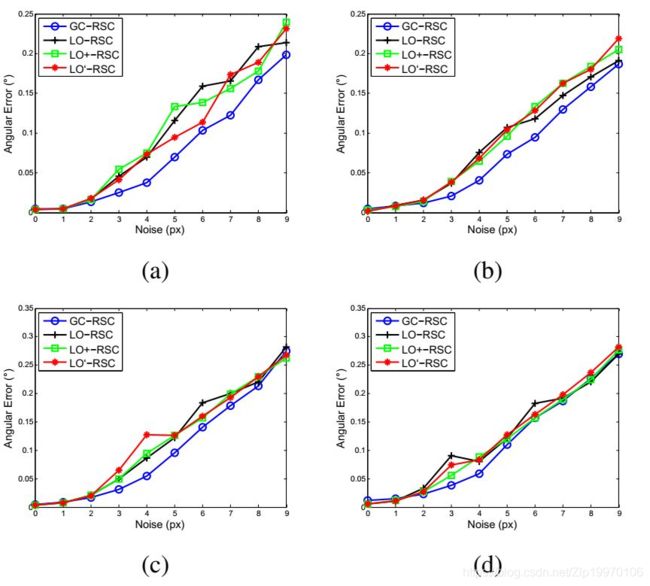
图2. 拟合出的直线的平均角度误差随噪声强度的变化曲线。对于每一个噪声强度,算法跑1000次。线的类型和野点数量为(a)直线,100%,(b)直线,500%,(c)虚线,100%,(d)虚线,500%。

表1. 在直线拟合和基本矩阵估算实验中,能得到正确解所需的最小内点采样比率。对于直线拟合实验,实验结果为所有实验的平均值——在三个不同的外点率(100%,500%,1000%)和不同噪声强度(0-9个像素)各运行1000次,因此总共运行了15000次。对于基本矩阵估算实验,实验结果为AdelaideRMF数据集上运行1000次的平均结果。
B. 基于真实图像数据的单应矩阵、仿射矩阵、基本矩阵以及本质矩阵的估计
具体实验条件及实验参数设置,请查阅原文。实验结果为:
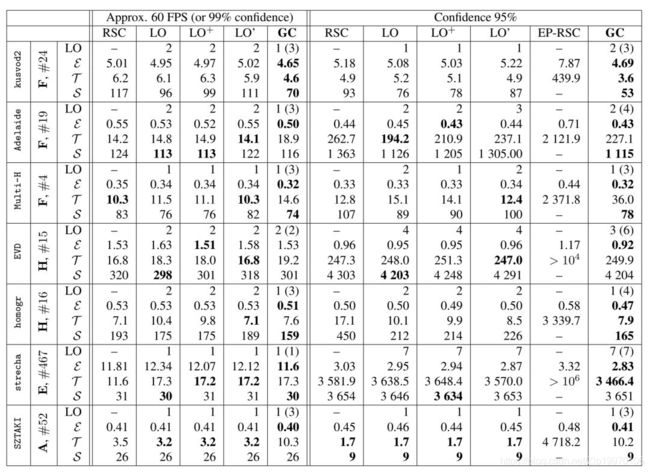
表2. 基本矩阵估算的数据集为:kusvod2 (24 对图片), AdelaideRMF (19 对图片) 和Multi-H (4 对图片);单应矩阵估计数据集为:homogr (16 对图片) 和EVD (15 对图片);本质矩阵估算数据集为:strecha (467 对图片),仿射变换估计数据集为:SZTAKI Earth Observation(52对图片)。因此,本文总共在597张图片中测试了提出的算法。前三列显示了数据集、问题(F/H/E/A)、图片对的数量。后五列为在99%置信度60FPS计算速度的限制下的测试结果(EP-RANSCA不受速度限制,因为它不能实时运行)。对于其他列,实验不设置时间限制,且置信度设为95%。结果为1000次运行的平均值。LO是局部优化的次数,括号中为图割算法运行的次数。模型的几何误差记录与第二行;平均的处理时间和需要的样本数记录在第三和第四行。对于基本矩阵和本质矩阵几何误差为 Sampson距离,对于单应矩阵和仿射矩阵,几何误差为投影误差。

图3. 单应矩阵、仿射矩阵、基本矩阵以及本质矩阵在不同数据集上的估计
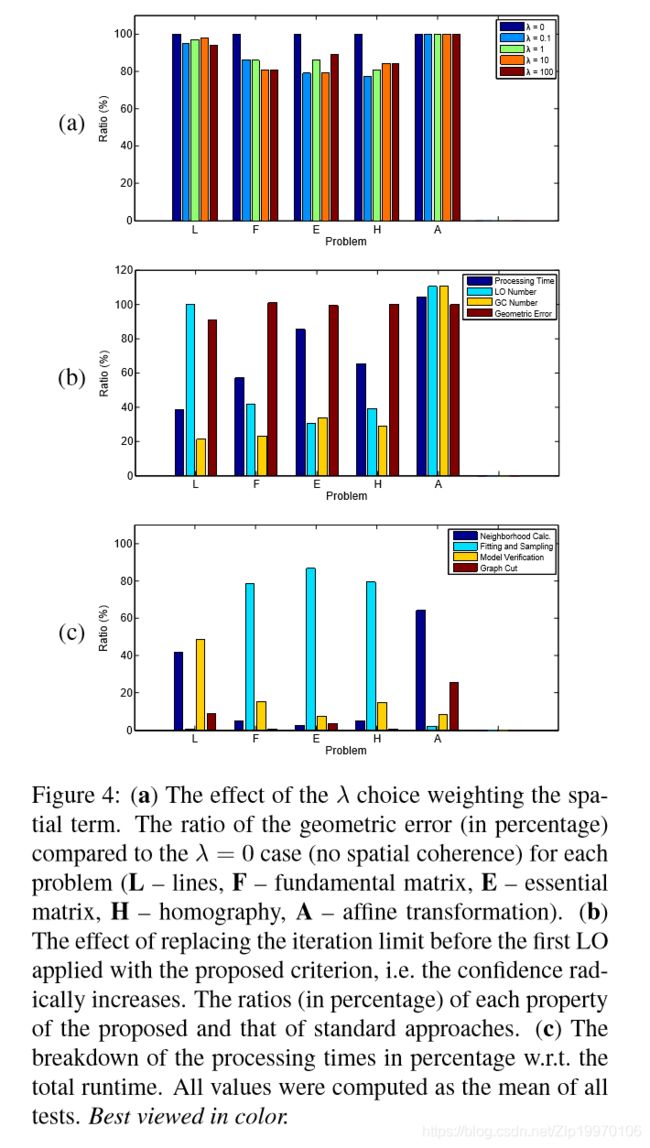
图4. 对 不 同 λ 对不同\lambda 对不同λ、局部优化算法及处理时间的性能评估
5. 参考文献
[1] D. Barath and J. Matas, “Graph-Cut RANSAC,” 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, 2018, pp. 6733-6741.