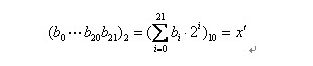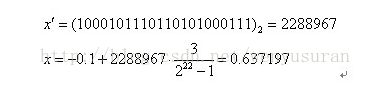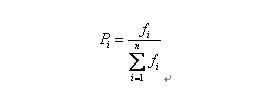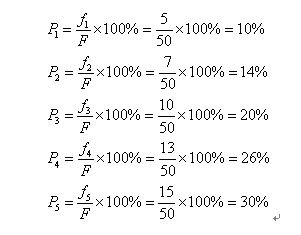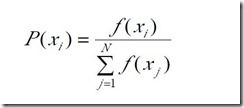遗传算法入门掌握
问题的提出与解决方案
已知一元函数:f(x)=x*sin(10π*x)+2.0 x∈[-1,2]
要求在既定的区间内找出函数的最大值
极大值、最大值、局部最优解、全局最优解
极大值在一个小邻域里面左边的函数值递增,右边的函数值递减,在图2.1里面的表现就是一个“山峰”。当然,在图上有很多个“山峰”,所以这个函数有很多个极大值。而对于一个函数来说,最大值就是在所有极大值当中,最大的那个。所以极大值具有局部性,而最大值则具有全局性。
因为遗传算法中每一条染色体,对应着遗传算法的一个 解决方案,一般我们用适应性函数(fitness function)来衡量这个解决方案的优劣。所以从一个基因组到其解的适应度形成一个映射。所以也可以把遗传算法的过程看作是一个在多元函数里面求最优解的过程。在这个多维曲面里面也有数不清的“山峰”,而这些最优解所对应的就是局部最优解。而其中也会有一个“山峰”的海拔最高的,那么这个就是全局最优解。而遗传算法的任务就是尽量爬到最高峰,而不是陷落在一些小山峰。(另外,值得注意的是遗传算法不一定要找“最高的山峰”,如果问题的适应度评价越小越好的话,那么全局最优解就是函数的最小值,对应的,遗传算法所要找的就是“最深的谷底”)
“袋鼠跳”问题
既然我们把 函数曲线理解成一个一个山峰和山谷组成的山脉。那么我们可以设想所得到的每一个解就是一只袋鼠,我们希望它们不断的向着更高处跳去,直到跳到最高的山峰(尽管袋鼠本身不见得愿意那么做)。所以求最大值的过程就转化成一个“袋鼠跳”的过程。下面介绍介绍“袋鼠跳”的几种方式。
爬山法、模拟退火和遗传算法
解决寻找最大值问题的几种常见的算法:
1. 爬山法(最速上升爬山法):
从搜索空间中随机产生邻近的点,从中选择对应解最优的个体,替换原来的个体,不断重复上述过程。因为只对“邻近”的点作比较,所以目光比较“短浅”,常常只能收敛到离开初始位置比较近的局部最优解上面。对于存在很多局部最优点的问题,通过一个简单的迭代找出全局最优解的机会非常渺茫。(在爬山法中,袋鼠最有希望到达最靠近它出发点的山顶,但不能保证该山顶是珠穆朗玛峰,或者是一个非常 高的山峰。因为一路上它只顾上坡,没有下坡。)
2. 模拟退火:
这个方法来自金属热加工过程的启发。在金属热加工过程中,当金属的温度超过它的熔点(Melting Point)时,原子就会激烈地随机运动。与所有的其它的物理系统相类似,原子的这种运动趋向于寻找其能量的极小状态。在这个能量的变迁过程中,开始时。温度非常高, 使得原子具有很高的能量。随着温度不断降低,金属逐渐冷却,金属中的原子的能量就越来越小,最后达到所有可能的最低点。利用模拟退火的时候,让算法从较大 的跳跃开始,使到它有足够的“能量”逃离可能“路过”的局部最优解而不至于限制在其中,当它停在全局最优解附近的时候,逐渐的减小跳跃量,以便使其“落脚 ”到全局最优解上。(在模拟退火中,袋鼠喝醉了,而且随机地大跳跃了很长时间。运气好的话,它从一个山峰跳过山谷,到了另外一个更高的山峰上。但最后,它渐渐清醒了并朝着它所在的峰顶跳去。)
3. 遗传算法:
模拟物竞天择的生物进化过程,通过维护一个潜在解的群体执行了多方向的搜索,并支持这些方向上的信息构成和交换。以面为单位的搜索,比以点为单位的搜索, 更能发现全局最优解。(在遗传算法中,有很多袋鼠,它们降落到喜玛拉雅山脉的任意地方。这些袋鼠并不知道它们的任务是寻找珠穆朗玛峰。但每过几年,就在一些海拔高度较低的地方射杀一些袋鼠,并希望存活下来的袋鼠是多产的,在它们所处的地方生儿育女。)(后来,一个叫天行健的网游给我想了 一个更恰切的故事:从前,有一大群袋鼠,它们被莫名其妙的零散地遗弃于喜马拉雅山脉。于是只好在那里艰苦的生活。海拔低的地方弥漫着一种无色无味的毒气,海拔越高毒气越稀薄。可是可怜的袋鼠们对此全然不觉,还是习惯于活蹦乱跳。于是,不断有袋鼠死于海拔较低的地方,而越 是在海拔高的袋鼠越是能活得更久,也越有机会生儿育女。就这样经过许多年,这些袋鼠们竟然都不自觉地聚拢到了一个个的山峰上,可是在所有的袋鼠中,只有聚拢到珠穆朗玛峰的袋鼠被带回了美丽的澳洲。)
下面主要介绍介绍遗传算法实现的过程。
遗传算法的实现过程
遗传算法的实现过程实际上就像自然界的进化过程那样。首先寻找一种对问题潜在解进行“数字化”编码的方案。(建立表现型和基因型的映射关系。)然后用随机数初始化一个种群(那么第一批袋鼠就被随意地分散在山脉上。),种群里面的个体就是这些数字化的编码。接下来,通过适当的解码过程之后,(得到袋鼠的位置坐标。)用适应性函数对每一个基因个体作一次适应度评估。(袋鼠爬得越高,越是受我们的喜爱,所以适应度相应越高。)用选择函数按照某种规定择优选择。(我们要每隔一段时间,在山上射杀一些所在海拔较低的袋鼠,以保证袋鼠总体数目持平。)让个体基因交叉变异。(让袋鼠随机地跳一跳)然后产生子代。(希望存活下来的袋鼠是多产的,并在那里生儿育女。)遗传算法并不保证你能获得问题的最优解,但是使用遗传算法的最大优点在于你不必去了解和操心如何去“找”最优解。(你不必去指导袋鼠向那边跳,跳多远。)而只要简单的“否定”一些表现不好的个体就行了。(把那些总是爱走下坡路的袋鼠射杀。)以后你会慢慢理解这句话,这是遗传算法的精粹!
所以我们总结出遗传算法的一般步骤:
开始循环直至找到满意的解。
1.评估每条染色体所对应个体的适应度。
2.遵照适应度越高,选择概率越大的原则,从种群中选择两个个体作为父方和母方。
3.抽取父母双方的染色体,进行交叉,产生子代。
4.对子代的染色体进行变异。
5.重复2,3,4步骤,直到新种群的产生。
结束循环。
接下来,我们将详细地剖析遗传算法过程的每一个细节。
编制袋鼠的染色体----基因的编码方式
通过前一章的学习,读者已经了解到人类染色体的编码符号集,由4种碱基的两种配合组成。共有4种情况,相当于2 bit的信息量。这是人类基因的编码方式,那么我们使用遗传算法的时候编码又该如何处理呢?
受到人类染色体结构的启发,我们可以设想一下,假设目前只有“0”,“1”两种碱基,我们也用一条链条把他们有序的串连在一起,因为每一个单位都能表现出 1bit的信息量,所以一条足够长的染色体就能为我们勾勒出一个个体的所有特征。这就是二进制编码法,染色体大致如下:
010010011011011110111110
上面的编码方式虽然简单直观,但明显地,当个体特征比较复杂的时候,需要大量的编码才能精确地描述,相应的解码过程(类似于生物学中的DNA翻译过程,就是把基因型映射到表现型的过程。)将过份繁复,为改善遗传算法的计算复杂性、提高运算效率,提出了浮点数编码。染色体大致如下:
1.2 – 3.3 – 2.0 –5.4– 2.7 – 4.3
那么我们如何利用这两种编码方式来为袋鼠的染色体编码呢?因为编码的目的是建立表现型到基因型的映射关系,而表现型一般就被理解为个体的特征。比如人的基因型是46条染色体所描述的(总长度 两 米的纸条?),却能解码成一个个眼,耳,口,鼻等特征各不相同的活生生的人。所以我们要想为“袋鼠”的染色体编码,我们必须先来考虑“袋鼠”的“个体特 征”是什么。也许有的人会说,袋鼠的特征很多,比如性别,身长,体重,也许它喜欢吃什么也能算作其中一个特征。但具体在解决这个问题的情况下,我们应该进一步思考:无论这只袋鼠是长短,肥瘦,只要它在低海拔就会被射杀,同时也没有规定身长的袋鼠能跳得远一些,身短的袋鼠跳得近一些。当然它爱吃什么就更不相 关了。我们由始至终都只关心一件事情:袋鼠在哪里。因为只要我们知道袋鼠在那里,我们就能做两件必须去做的事情:
(1)通过查阅喜玛拉雅山脉的地图来得知袋鼠所在的海拔高度(通过自变量求函数值。)以判断我们有没必要把它射杀。
(2)知道袋鼠跳一跳后去到哪个新位置。
如 果我们一时无法准确的判断哪些“个体特征”是必要的,哪些是非必要的,我们常常可以用到这样一种思维方式:比如你认为袋鼠的爱吃什么东西非常必要,那么你 就想一想,有两只袋鼠,它们其它的个体特征完全同等的情况下,一只爱吃草,另外一只爱吃果。你会马上发现,这不会对它们的命运有丝毫的影响,它们应该有同等的概率被射杀!只因它们处于同一个地方。(值得一提的是,如果你的基因编码设计中包含了袋鼠爱吃什么的信息,这其实不会影响到袋鼠的进化的过程,而那只 攀到珠穆朗玛峰的袋鼠吃什么也完全是随机的,但是它所在的位置却是非常确定的。)
以上是对遗传算法编码过程中经常经历的思维过程,必须把具体问题抽象成数学模型,突出主要矛盾,舍弃次要矛盾。只有这样才能简洁而有效的解决问题。希望初学者仔细琢磨。
既然确定了袋鼠的位置作为个体特征,具体来说位置就 是横坐标。那么接下来,我们就要建立表现型到基因型的映射关系。就是说如何用编码来表现出袋鼠所在的横坐标。由于横坐标是一个实数,所以说透了我们就是要对这个实数编码。回顾我们上面所介绍的两种编码方式,读者最先想到的应该就是,对于二进制编码方式来说,编码会比较复杂,而对于浮点数编码方式来说,则会比较简洁。恩,正如你所想的,用浮点数编码,仅仅需要一个浮点数而已。而下面则介绍如何建立二进制编码到一个实数的映射。
明显地,一定长度的二进制编码序列,只能表示一定精度的浮点数。譬如我们要求解精确到六位小数,由于区间长度为2 – (-1) = 3 ,为了保证精度要求,至少把区间[-1,2]分为3 × 106等份。又因为
所以编码的二进制串至少需要22位。
把一个二进制串(b0,b1,....bn)转化位区间里面对应的实数值通过下面两个步骤。
(1)将一个二进制串代表的二进制数转化为10进制数:
(2)对应区间内的实数:
例如一个二进制串<1000101110110101000111>表示实数值0.637197。
二进制串<0000000000000000000000>和<1111111111111111111111>则分别表示区间的两个端点值-1和2。
由于往下章节的示例程序几乎都只用到浮点数编码,所以这个“袋鼠跳”问题的解决方案也是采用浮点数编码的。往下的程序示例(包括装载基因的类,突变函数)都是针对浮点数编码的。(对于二进制编码这里只作简单的介绍,不过这个“袋鼠跳”完全 可以用二进制编码来解决的,而且更有效一些。所以读者可以自己尝试用二进制编码来解决。)
我们定义一个类作为袋鼠基因的载体。(细心的人会提 出这样的疑问:为什么我用浮点数的容器来储藏袋鼠的基因呢?袋鼠的基因不是只用一个浮点数来表示就行吗?恩,没错,事实上对于这个实例,我们只需要用上一个浮点数就行了。我们这里用上容器是为了方便以后利用这些代码处理那些编码需要一串浮点数的问题。)
class Genome
{
public:
friend class GenAlg;
friend class GenEngine;
Genome():fitness(0){}
Genome(vector <double> vec, double f): vecGenome(vec), fitness(f){} //类的带参数初始化参数。
private:
vector <double> vecGenome; // 装载基因的容器
double fitness; //适应度
};
物竞天择--适应性评分与及选择函数。
1.物竞――适应度函数(fitness function)
自然界生物竞争过程往往包含两个方面:生物相互间的搏斗与及生物与客观环境的搏斗过程。但在我们这个实例里面,你可以想象到,袋鼠相互之间是非常友好的,它们并不需要互相搏斗以争取生存的权利。它们的生死存亡更多是取决于你的判断。因为你要衡量哪只袋鼠该杀,哪只袋鼠不该杀,所以你必须制定一个衡量的标 准。而对于这个问题,这个衡量的标准比较容易制定:袋鼠所在的海拔高度。(因为你单纯地希望袋鼠爬得越高越好。)所以我们直接用袋鼠的海拔高度作为它们的 适应性评分。即适应度函数直接返回函数值就行了。
2.天择――选择函数(selection)
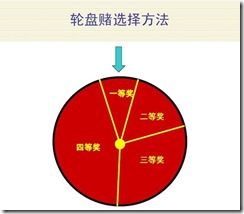
自然界中,越适应的个体就越有可能繁殖后代。但是也不能说适应度越高的就肯定后代越多,只能是从概率上来说更多。(毕竟有些所处海拔高度较低的袋鼠很幸运,逃过了你的眼睛。)那么我们怎么来建立这种概率关系呢?下面我们介绍一种常用的选择方法――轮盘赌(Roulette Wheel Selection)选择法。假设种群数目,某个个体其适应度为,则其被选中的概率为:
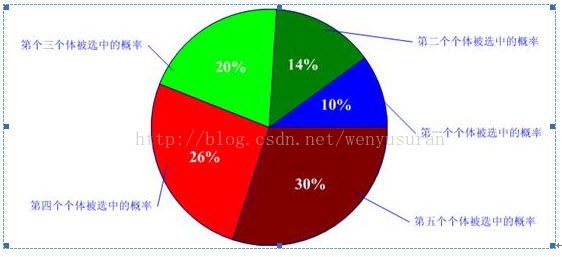
比如我们有5条染色体,他们所对应的适应度评分分别为:5,7,10,13,15。
所以累计总适应度为:
所以各个个体被选中的概率分别为:
呵呵,有人会问为什么我们把它叫成轮盘赌选择法啊?其实你只要看看图2-2的轮盘就会明白了。这个轮盘是按照各个个体的适应度比例进行分块的。你可以想象一下,我们转动轮盘,轮盘停下来的时候,指针会随机地指向某一个个体所代表的区域,那么非常幸运地,这个个体被选中了。(很明显,适应度评分越高的个体被 选中的概率越大。)
那么接下来我们看看如何用代码去实现轮盘赌。
Genome GenAlg:: GetChromoRoulette()
{
//产生一个0到人口总适应性评分总和之间的随机数.
//中m_dTotalFitness记录了整个种群的适应性分数总和)
double Slice = (random()) * totalFitness;
//这个基因将承载转盘所选出来的那个个体.
Genome TheChosenOne;
//累计适应性分数的和.
double FitnessSoFar = 0;
//遍历总人口里面的每一条染色体。
for (int i=0; i<popSize; ++i)
{
//累计适应性分数.
FitnessSoFar += vecPop[i].fitness;
//如果累计分数大于随机数,就选择此时的基因.
if (FitnessSoFar >= Slice)
{
TheChosenOne = vecPop[i];
break;
}
}
//返回转盘选出来的个体基因
return TheChosenOne;
}
遗传变异――基因重组(交叉)与基因突变。
应该说这两个步骤就是使到子代不同于父代的根本原因(注意,我没有说是子代优于父代的原因,只有经过自然的选择后,才会出现子代优于父代的倾向。)。对于这两种遗传操作,二进制编码和浮点型编码在处理上有很大的差异,其中二进制编码的遗传操作过程,比较类似于自然界里面的过程,下面将分开讲述。
1.基因重组/交叉(recombination/crossover)
(1)二进制编码
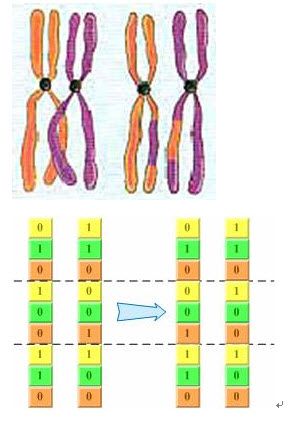
回顾上一章介绍的基因交叉过程:同源染色体联会的过程中,非姐妹染色单体(分别来自父母双方)之间常常发生交叉,并且相互交换一部分染色体,如图2-3。 事实上,二进制编码的基因交换过程也非常类似这个过程――随机把其中几个位于同一位置的编码进行交换,产生新的个体,如图2-4所示。
(2)浮点数编码
如果一条基因中含有 多个浮点数编码,那么也可以用跟上面类似的方法进行基因交叉,不同的是进行交叉的基本单位不是二进制码,而是浮点数。而如果对于单个浮点数的基因交叉,就有其它不同的重组方式了,比如中间重组:
这样只要随机产生就能得到介于父代基因编码值和母代基因编码值之间的值作为子代基因编码的值。
考 虑到“袋鼠跳”问题的具体情况――袋鼠的个体特征仅仅表现为它所处的位置。可以想象,同一个位置的袋鼠的基因是完全相同的,而两条相同的基因进行交叉后,相当于什么都没有做,所以我们不打算在这个例子里面使用交叉这一个遗传操作步骤。(当然硬要这个操作步骤也不是不行的,你可以把两只异地的袋鼠捉到一起, 让它们交配,然后产生子代,再把它们送到它们应该到的地方。)
2.基因突变(Mutation)
(1)二进制编码
同样回顾一下上一章所介绍的基因突变过程:基因突变是染色体的某一个位点上基因的改变。基因突变使一个基因变成它的等位基因,并且通常会引起一定的表现型变化。恩,正如上面所说,二进制编码的遗传操作过程和生物学中的过程非常相类似,基因串上的“ 0”或“ 1”有一定几率变成与之相反的“ 1”或“ 0”。例如下面这串二进制编码:
101101001011001
经过基因突变后,可能变成以下这串新的编码:
001101011011001
(2)浮点型编码
浮点型编码的基因突变过程一般是对原来的浮点数增加或者减少一个小随机数。比如原来的浮点数串如下:
1.2,3.4, 5.1, 6.0,4.5
变异后,可能得到如下的浮点数串:
1.3,3.1, 4.9, 6.3,4.4
当 然,这个小随机数也有大小之分,我们一般管它叫“步长”。(想想“袋鼠跳”问题,袋鼠跳的长短就是这个步长。)一般来说步长越大,开始时进化的速度会比较 快,但是后来比较难收敛到精确的点上。而小步长却能较精确的收敛到一个点上。所以很多时候为了加快遗传算法的进化速度,而又能保证后期能够比较精确地收敛到最优解上面,会采取动态改变步长的方法。其实这个过程与前面介绍的模拟退火过程比较相类似,读者可以做简单的回顾。
下面是针对浮点型编码的基因突变函数的写法:
void GenAlg::Mutate(vector<double> &chromo)
{
//遵循预定的突变概率,对基因进行突变
for (int i=0; i<chromo.size(); ++i)
{
//如果发生突变的话
if (random() < mutationRate)
{
//使该权值增加或者减少一个很小的随机数值
chromo[i] += ((random()-0.5) * maxPerturbation);
//保证袋鼠不至于跳出自然保护区.
if(chromo[i] < leftPoint)
{
chromo[i] = rightPoint;
}
else if(chromo[i] > rightPoint)
{
chromo[i] = leftPoint;
}
//以上代码非基因变异的一般性代码只是用来保证基因编码的可行性。
}
}
}
值得一提的是遗传算法中基因突变的特点和上一章提到的生物学中的基因突变的特点非常相类似,这里回顾一下:
1.基因突变是随机发生的,且突变频率很低。(不过某些应用中需要高概率的变异)
2.大多数基因变异对生物本身是有害的。
3.基因突变是不定向的。
好了,到此为止,基因编码,基因适应度评估,基因选择,基因变异都一一实现了,剩下来的就是把这些遗传过程的“零件”装配起来了。
遗传算法引擎――GenAlg
<span style="font-size:16px;">/遗传算法
class GenAlg
{
public:
//这个容器将储存每一个个体的染色体
vector <Genome> vecPop;
//人口(种群)数量
int popSize;
//每一条染色体的基因的总数目
int chromoLength;
//所有个体对应的适应性评分的总和
double totalFitness;
//在所有个体当中最适应的个体的适应性评分
double bestFitness;
//所有个体的适应性评分的平均值
double averageFitness;
//在所有个体当中最不适应的个体的适应性评分
double worstFitness;
//最适应的个体在m_vecPop容器里面的索引号
Genome fittestGenome;
//基因突变的概率,一般介于0.05和0.3之间
double mutationRate;
//基因交叉的概率一般设为0.7
double crossoverRate;
//代数的记数器
int generation;
//最大变异步长
double maxPerturbation;
double leftPoint;
double rightPoint;
//构造函数
GenAlg();
//初始化变量
void Reset();
//初始化函数
void init(int popsize, double MutRate, double CrossRate, int GenLenght,double LeftPoint,double RightPoint);
//计算TotalFitness, BestFitness, WorstFitness, AverageFitness等变量
void CalculateBestWorstAvTot();
//轮盘赌选择函数
Genome GetChromoRoulette();
//基因变异函数
void Mutate(vector<double> &chromo);
//这函数产生新一代基因
void Epoch(vector<Genome> &vecNewPop);
Genome GetBestFitness();
double GetAverageFitness();
};</span>
其中Reset()函数,init()函数和CalculateBestWorstAvTot()函数都比较简单,读者查看示例程序的代码就能明白了。而下面分别介绍init函数和Epoch函数。
类的初始化函数――init函数
init函数主要充当CGenAlg类的初始化工作,把一些成员变量都变成可供重新开始遗传算法的状态。(为什么我不在构造函数里面做这些工作呢?因为我的程序里面CGenAlg类是View类的成员变量,只会构造一次,所以需要另外的初始化函数。)下面是init函数的代码:
void GenAlg::init(int popsize, double MutRate, double CrossRate, int GenLenght,double LeftPoint,double RightPoint)
{
popSize = popsize;
mutationRate = MutRate;
crossoverRate = CrossRate;
chromoLength = GenLenght;
totalFitness = 0;
generation = 0;
//fittestGenome = 0;
bestFitness = 0.0;
worstFitness = 99999999;
averageFitness = 0;
maxPerturbation=0.004;
leftPoint=LeftPoint;
rightPoint=RightPoint;
//清空种群容器,以初始化
vecPop.clear();
for (int i=0; i<popSize; i++)
{
//类的构造函数已经把适应性评分初始化为0
vecPop.push_back(Genome());
//把所有的基因编码初始化为函数区间内的随机数。
for (int j=0; j<chromoLength; j++)
{
vecPop[i].vecGenome.push_back(random() *
(rightPoint - leftPoint) + leftPoint);
}
}
}
恩,正如我之前说的,我们这个程序不但要应付基因编码只有一个浮点数的“袋鼠跳”问题的情况,还希望以后在处理一串浮点数编码的时候也一样适用,所以从这里开始我们就把基因当成串来对待。
开创新的纪元――Epoch函数
现在万事具备了,只差把所有现成的“零件”装配起来而已。而Epoch函数就正好充当这个职能。下面是这个函数的实现:
void GenEngine:: OnStartGenAlg()
{
//产生随机数
srand( (unsigned)time( NULL ) );
//初始化遗传算法引擎
genAlg.init(g_popsize, g_dMutationRate, g_dCrossoverRate, g_numGen,g_LeftPoint,g_RightPoint);
//清空种群容器
m_population.clear();
//种群容器装进经过随机初始化的种群
m_population = genAlg.vecPop;
//定义两个容器,以装进函数的输入与及输出(我们这个函数是单输入单输出的,但是以后往往不会那么简单,所以我们这里先做好这样的准备。)
vector <double> input;
double output;
input.push_back(0);
for(int Generation = 0;Generation <= g_Generation;Generation++)
{
//里面是对每一条染色体进行操作
for(int i=0;i<g_popsize;i++)
{
input = m_population[i].vecGenome;
//为每一个个体做适应性评价,如之前说的,评价分数就是函数值。其
//Function函数的作用是输入自变量返回函数值,读者可以参考其代码。
output = (double)curve.function(input);
m_population[i].fitness = output;
}
//由父代种群进化出子代种群(长江后浪退前浪。)
genAlg.Epoch(m_population);
//if(genAlg.GetBestFitness().fitness>=bestFitness)
bestSearch=genAlg.GetBestFitness().vecGenome[0];
bestFitness=genAlg.GetBestFitness().fitness;
averageFitness=genAlg.GetAverageFitness();
//cout<<bestSearch<<endl;
report(Generation+1);
}
//return bestSearch;
}
让袋鼠在你的电脑里进化――程序的运行
我想没有什么别的方法比自己亲手写一个程序然后通过修改相关参数不断调试程序,更能理解并且掌握一种算法了。不知道你还记不记得你初学程序的日子,我想你上机动手写程序比坐在那里看一本厚厚的程序开发指南效率不知高上多少倍,兴趣也特命浓厚,激情也特别高涨。恩,你就是需要那样的感觉,学遗传算法也是一样 的。你需要把自己的代码运行起来,然后看看程序是否按照你所想象的去运行,如果没有,你就要思考原因,按照你的想法去改善代码,试着去弄清其中的内在联系。这是一个思维激活的过程,你大脑中的神经网络正在剧烈抖动(呵呵,或许学到后面你就知道你大脑的神经网络是如何“抖动”的。),试图去接受这新鲜而有 趣的知识。遗传算法(包括以后要学到的人工神经网络)包含大量的可控参数,比如进化代数、人口数目、选择概率、交叉概率、变异概率、变异的步长还有以后学到的很多。这些参数之间的搭配关系,不能指望别人用“灌输”的方式让你被动接受,这需要你自己在不断的尝试,不断的调整中去形成一种“感觉”的。很多时候 一个参数的量变在整个算法中会表现出质的变化。而算法的效果又能从宏观上反映参数的设置。
现在就让我们来对这个程序做简单的说明。
参数的设置:
这个程序有很多的需要预先设置好的参数,为了方便修改,我把它们都定义为全局变量,定义和初始化都放在Parameter.h的头文件里面。下面对几个主要参数的说明:
- //目标函数的左右区间,目前的设置是[-1,2]
- double g_LeftPoint = -1;
- double g_RightPoint = 2;
- ////遗传算法相关参数////
- int g_numGen = 1; //每条染色体的编码个数,这里是1个
- int g_Generation = 1000; //进化的代数
- int g_popsize = 50; //种群的人口数目(就是说你要放多少只袋鼠到山上)
- double g_dMutationRate = 0.8; //基因变异的概率
- double g_dMaxPerturbation = 0.005; //基因变异的步长(袋鼠跳的最大距离)
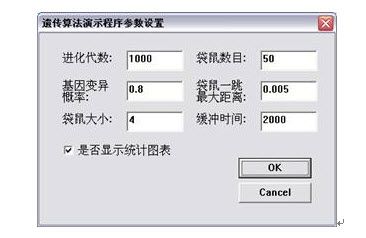
当然,一些主要的参数在程序运行后可以通过参数设置选项进行设置。(其中缓冲时间是每进化一代之后,暂停的时间,单位为毫秒)如图2-6。
运行程序:
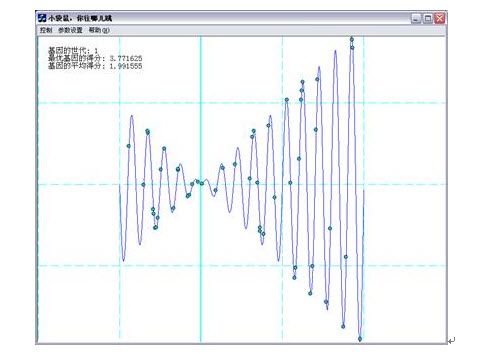
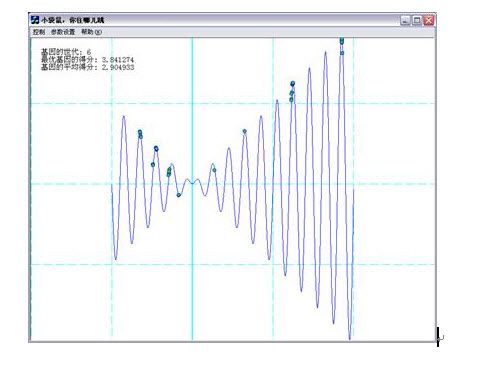
程序运行后请选择菜单项:控制->让袋鼠们开始跳吧,开始遗传算法的过程。其中蓝色的线条是函数曲线(恩,那就是喜玛拉雅山脉。其中最高的波峰,就是珠穆朗玛峰。)绿色的点是一只只袋鼠。上方的黑色曲线图表是对每一代最优的个体的适应性评分的统计图表。下方的黑色曲线图表是对每一代所有个体的平均适应性评分的统计图表。(如果你认为它们阻碍了你的视线,你可以在参数设置里面取消掉。)如图2-7所示。另外还可以用键盘的上下左右键来控制视窗的移动,加减键控制函数曲线的放缩。
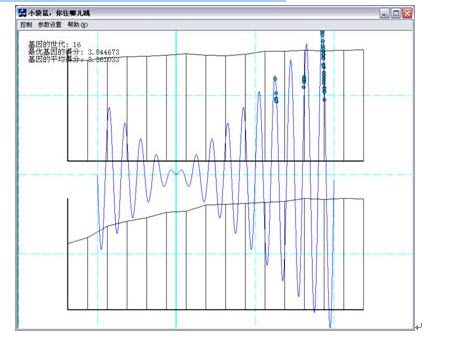
刚开始的时候,袋鼠分布得比较分散它们遍布了各个山岭,有的在高峰上,有的在深谷里。(如图2-8)
经过了几代的进化后,一些海拔高度比较低的都被我们射杀了,而海拔较高的袋鼠却不断的生儿育女。(如图2-9)
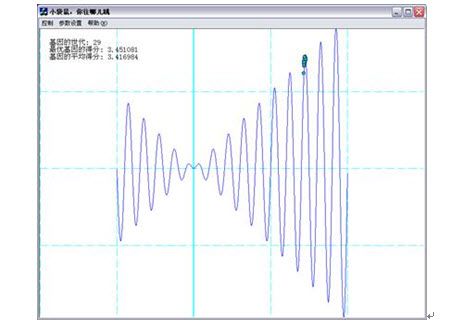
最后整个袋鼠种群就只出现在最高峰上面(最优解上)。(如图2-10)
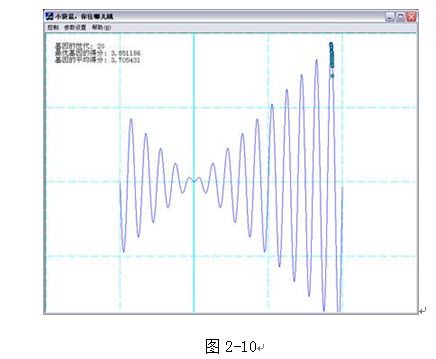
当然,袋鼠不是每一次都能跳到珠穆朗玛峰的,如图2-11所 示。(就是说不是每次都能收敛到最优解)也许它们跳到了某一个山峰,就自大的认为它们已经“会当凌绝顶”了。(当然,事实上是因为不管它们向前还是向后跳都只能得到更小的适应度,所以不等它们跳过山谷,再跳到旁边更高的山峰,就被我们射杀了。)所以,我们为了使到袋鼠每次都尽可能的攀到珠穆朗玛峰,而不是 留恋在某一个低一些的山峰,我们有两个改进的办法,其一是初始人口数目更多一些,以使最好有一些袋鼠一开始就降落到最高峰的附近,但是这种方法对于搜索空间非常大的问题往往是无能为力的。我们常常采用的方法是使袋鼠有一定的概率跳一个很大的步长,以使袋鼠有可能跳过一个山谷到更高的山峰去。这些改进的方法 留给读者自己去实现。
另外,如果把变异的机率调得比较高,那么就会出现袋鼠跳得比较活跃的局面,但是很可能丢失了最优解;而如果变异的机率比较低的话,袋鼠跳得不太活跃,找到最优解的速度就会慢一些,这也留给读者自己去体验。
作为一个寻找大值的程序,这个的效率还 很低。我希望留给初学者更多改进的空间,大家不必受限于现有的方法,大可以发挥丰富的想象力,自己想办法去提高程序的效率,然后自己去实现它,让事实去验证你的想法是否真的能提高效率,抑或刚好相反。恩,在这个过程当中,大家不知不觉地走进了遗传算法的圣殿了,胜于一切繁复公式的摆设和教条式的讲解。
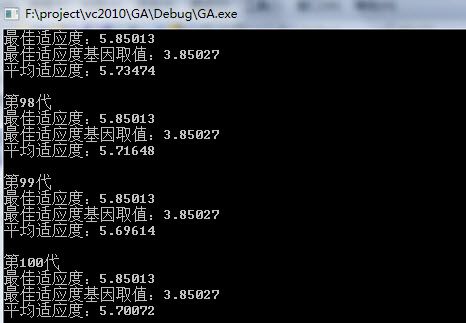
博主后记:由于原作者未知加上本人学习繁忙,所以MFC版本源码未整理,以下为自己整理实现的控制台演示版本:
最后结果是一样的,附上下载:
http://download.csdn.net/detail/emiyasstar__/3759299
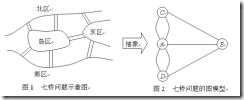
旅行商问题(TSF)
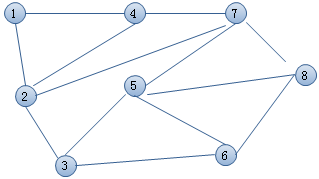
TSP问题实际上是”哈密顿回路问题”中的”哈密顿最短回路问题”.如下图,就是要把下面8个城市不重复的全部走一遍。有点像小时候玩的画笔画游戏,一笔到底不能重复。TSP不光是要求全部走一遍,并且是要求路径最短。就是有可能全部走一遍有很多走法,要找出其中总路程最短的走法。
和这个问题有点相似的是欧拉回路(下图)问题,它不是要求把每个点都走一遍,而是要求把每个边都不重复走一遍(点可以重复),当然欧拉回路不是本算法研究的范畴。
本文会从TSP引申出下面系列问题
1、 TSP问题:要求每个点都遍历到,而且要求每个点只被遍历一次,并且总路程最短。
2、 最短路径问题:要求从城市1 到城市8,找一条最短路径。
3、 遍历m个点,要求找出其距离最短的路线。(如果m=N总数,其实就是问题1了,所以问题1可以看成是问题3的特例 )。
遗传算法的理论是根据达尔文进化论而设计出来的算法: 人类是朝着好的方向(最优解)进化,进化过程中,会自动选择优良基因,淘汰劣等基因。
在上面tsp问题中,一个城市节点可以看成是一个基因,一个最优解就是一条路径,包含若干个点。就类似一条染色体有若干基因组成一样。所以求最短路径问题,可以抽象成求最优染色体的问题。
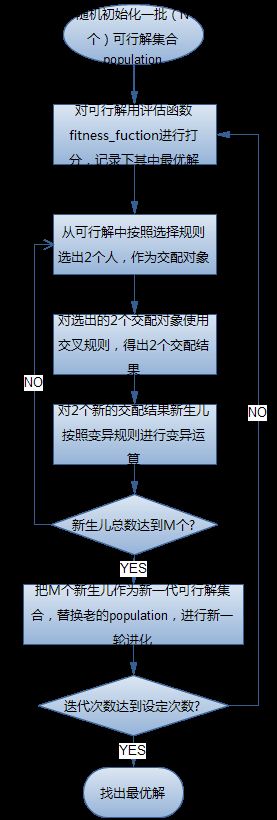
遗传算法很简单,没有什么分支判断,只有两个大循环,流程大概如下
流程中有几个关键元素:
1、 适度值评估函数。这个函数是算法的关键,就是对这个繁衍出来的后代进行评估打分,是优秀,还是一般,还是很差的畸形儿。用这个函数进行量化。在tsp中,路径越短,分数越高。函数可以可以这样 fitness = 1/total_distance. 或者 fitness = MAX_DISTANCE – total_distance. 不同的计算方法会影响算法的收敛速度,直接影响结果和性能。
2、 选择运算规则: 又称选择算子。对应着达尔文理论中适者生存,也有地方叫着精英主义原则,意思就是只有优秀的人才有更大的几率存活下来,拥有交配权。有权利拥有更多后代,传承下自己血脉基因。和现实中很相像,皇帝权臣遗留下来的子孙后代比较多。选择方法比较多。最常见的是round robin selection 算法,即轮盘赌算法, 这个算法比较简单有效。选择算法目前已有的有10来种之多。各种不同业务可以按需选择。
选择公式如下:
- //选择运算---轮盘赌,此算法要求不能有负数.
- int32_t Genetic::Selection(Genome& selGenome)
- {
- //生成一个随机浮点数
//本算法在轮盘赌算法上加上了选择概率,提高最大可行解入围概率 - double ftmp = (((random())%100001)/(100000+ 0.0000001));
- if( ftmp> 0.9 )
- {
- GetBestGenome(selGenome);
- return ESUCCESS;
- }
- //生成一个【0, m_dTotalFitness】之间的随机浮点数
- double dRange = (((random()+ random())%100001)/(100000+ 0.0000001))* m_dTotalFitness;
- double dCursor = 0.0;
- size_t i = 0;
-
- for(i= 0; i < m_vGenome.size();++i)
- {
- dCursor += m_vGenome[i].dFitness;
-
- if (dCursor > dRange)
- {
- break;
- }
- }
- selGenome = m_vGenome[i];
-
- return ESUCCESS;
- }
3、 交叉运算规则:又称交配规则,交叉算子。对应遗传学中的精子和卵子产生的受精卵含有精子的部分基因,也含有卵子的部分基因的现象。就像孩子有点像父亲,又有点像母亲的规律。交叉运算算法更多。作者可以天马行空的自己去想象。只要达到交叉结果中含有父母的基因就可以。最常见的是k-opt 交换。其中k可以是 1,2,3….等等。简称单点交换,两点交换,3点交换等等:
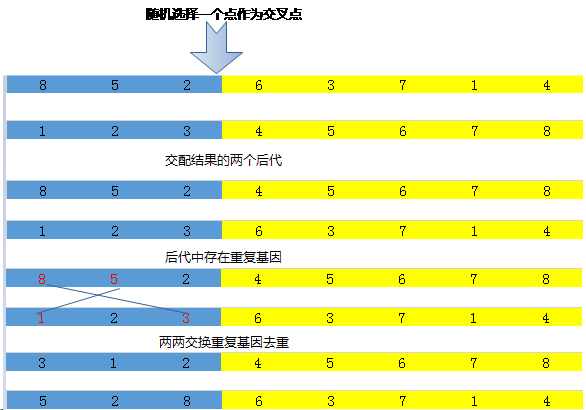
单点交换
其中修复重复基因根据业务需要看是否需要。
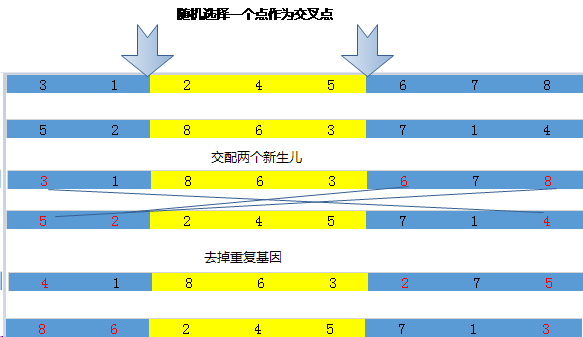
两点交换
4、 变异运算规则:又叫变异算子。在人类遗传进化过程中。会发生一些基因突变。这些突变有可能是好的突变,有可能是坏的突变。像癌细胞就是坏的突变。爱因斯坦的大脑估计是好的突变。突变方法也是可以天马行空的自己去发挥创造。
这里讨论一下,为什么要有突变这道流程呢。从人类进化角度来说。人类基因有数十万种,在远古交流比较少的年代。都是部落内部通婚,但是整个部落内部居民可能都缺少某种好的基因,这样无论他们怎么交配,都不会产生好的基因,那么他们需要引入好的基因,于是和其他部落通婚。引入其他自己没有的基因,其实对于这个种群来说这就是一次基因变异。如果是好的变异,那么这个后代就很优秀,结果就是会产生更多子孙,把这个好的变异基因传承下去,如果不是好的变异基因,自然而然会在前面选择算子下淘汰,就是现实生活中的所谓的年幼夭折,痴呆无后,或先天畸形被淘汰,不会传承下去。
从计算机算法角度看:所有的启发式算法无外乎2种手段结合。局域搜索和全域搜索。局域搜索是在邻域范围内找出最优解。对应的是选择算子和交叉算子。在自己部落里面找最优秀的人。如果只有局域搜索的话,就容易陷入局域最优解。算法结果肯定是要找出全域最优解。这就要求跳出局域搜索。我们称之为“创新”。创新就是一次打破常规的突破——就是我们的“变异”算子。
这里拿最短路径路径举例子,求点1到点8之间的最短路径, 初始解是1——2——3——6——8
内变异:所谓内变异就是在自己内部发生变异。严格来说其实不是一种变异。但是它又是一种比较有效的手段。
外变异:外变异是引入创新,突破传统的质的飞跃, 也是启发算法中所谓的全域搜索。下面是充当前基因中引入外部基因(当前集合的补集)。
![]()
结尾:遗传算法除了上述这些几个主要算子之外,还有一些细节。如交叉概率pc,变异概率pm,这些虽然都是辅助手段,但是有时候对整个算法结果和性能带来截然不同的效果。这也是启发式算法的一个缺点。参数需要不停的在实践中摸索,没有万能的推荐参数。
还有细心的读者可能发现几个疑问,就是最短路径中变异或交叉结果可能产生无效解,如前面最短路径 1——6——3——2——8. 其中1和6之间根本没有通路。碰到这种情况,可以抛弃这条非法解,重新生成一条随机新解(其实这也是一次变异创新)。或者自己修复成可行解。反正框框在那里。具体手段可以自己天马行空发挥。
另一个比较实际的问题是:在最短路径中并不知道染色体长度是多少,不错。大部分人还是用定长染色体去解决问题,这样性能低下。算法不直观。这时候可以使用变长染色体来解决。其实我建议不管何种情况,都设计变长染色体模式。因为定长也是变长的一种特例。使用变长可以解决任何问题。不管是tsp还是最短路径问题。
还有一个编解码问题,就是把现实问题转换成基因,这些问题都比较容易解决,最简单的就是直接用数组下标表示。
优化算法入门系列文章目录(更新中):
1. 模拟退火算法
2. 遗传算法
遗传算法 ( GA , Genetic Algorithm ) ,也称进化算法 。 遗传算法是受达尔文的进化论的启发,借鉴生物进化过程而提出的一种启发式搜索算法。因此在介绍遗传算法前有必要简单的介绍生物进化知识。
一.进化论知识
作为遗传算法生物背景的介绍,下面内容了解即可:
种群(Population):生物的进化以群体的形式进行,这样的一个群体称为种群。
个体:组成种群的单个生物。
基因 ( Gene ) :一个遗传因子。
染色体 ( Chromosome ) :包含一组的基因。
生存竞争,适者生存:对环境适应度高的、牛B的个体参与繁殖的机会比较多,后代就会越来越多。适应度低的个体参与繁殖的机会比较少,后代就会越来越少。
遗传与变异:新个体会遗传父母双方各一部分的基因,同时有一定的概率发生基因变异。
简单说来就是:繁殖过程,会发生基因交叉( Crossover ) ,基因突变 ( Mutation ) ,适应度( Fitness )低的个体会被逐步淘汰,而适应度高的个体会越来越多。那么经过N代的自然选择后,保存下来的个体都是适应度很高的,其中很可能包含史上产生的适应度最高的那个个体。
二.遗传算法思想
借鉴生物进化论,遗传算法将要解决的问题模拟成一个生物进化的过程,通过复制、交叉、突变等操作产生下一代的解,并逐步淘汰掉适应度函数值低的解,增加适应度函数值高的解。这样进化N代后就很有可能会进化出适应度函数值很高的个体。
举个例子,使用遗传算法解决“0-1背包问题”的思路:0-1背包的解可以编码为一串0-1字符串(0:不取,1:取) ;首先,随机产生M个0-1字符串,然后评价这些0-1字符串作为0-1背包问题的解的优劣;然后,随机选择一些字符串通过交叉、突变等操作产生下一代的M个字符串,而且较优的解被选中的概率要比较高。这样经过G代的进化后就可能会产生出0-1背包问题的一个“近似最优解”。
编码:需要将问题的解编码成字符串的形式才能使用遗传算法。最简单的一种编码方式是二进制编码,即将问题的解编码成二进制位数组的形式。例如,问题的解是整数,那么可以将其编码成二进制位数组的形式。将0-1字符串作为0-1背包问题的解就属于二进制编码。
遗传算法有3个最基本的操作:选择,交叉,变异。
选择:选择一些染色体来产生下一代。一种常用的选择策略是 “比例选择”,也就是个体被选中的概率与其适应度函数值成正比。假设群体的个体总数是M,那么那么一个体Xi被选中的概率为f(Xi)/( f(X1) + f(X2) + …….. + f(Xn) ) 。比例选择实现算法就是所谓的“轮盘赌算法”( Roulette Wheel Selection ) ,轮盘赌算法的一个简单的实现如下:
/* * 按设定的概率,随机选中一个个体 * P[i]表示第i个个体被选中的概率 */ int RWS() { m = 0; r =Random(0,1); //r为0至1的随机数 for(i=1;i<=N; i++) { /* 产生的随机数在m~m+P[i]间则认为选中了i * 因此i被选中的概率是P[i] */ m = m + P[i]; if(r<=m) return i; } }
交叉(Crossover):2条染色体交换部分基因,来构造下一代的2条新的染色体。例如:
交叉前:
00000|011100000000|10000
11100|000001111110|00101
交叉后:
00000|000001111110|10000
11100|011100000000|00101
染色体交叉是以一定的概率发生的,这个概率记为Pc 。
变异(Mutation):在繁殖过程,新产生的染色体中的基因会以一定的概率出错,称为变异。变异发生的概率记为Pm 。例如:
变异前:
000001110000000010000
变异后:
000001110000100010000
适应度函数 ( Fitness Function ):用于评价某个染色体的适应度,用f(x)表示。有时需要区分染色体的适应度函数与问题的目标函数。例如:0-1背包问题的目标函数是所取得物品价值,但将物品价值作为染色体的适应度函数可能并不一定适合。适应度函数与目标函数是正相关的,可对目标函数作一些变形来得到适应度函数。
三.基本遗传算法的伪代码
/* * Pc:交叉发生的概率 * Pm:变异发生的概率 * M:种群规模 * G:终止进化的代数 * Tf:进化产生的任何一个个体的适应度函数超过Tf,则可以终止进化过程 */ 初始化Pm,Pc,M,G,Tf等参数。随机产生第一代种群Pop do { 计算种群Pop中每一个体的适应度F(i)。 初始化空种群newPop do { 根据适应度以比例选择算法从种群Pop中选出2个个体 if ( random ( 0 , 1 ) < Pc ) { 对2个个体按交叉概率Pc执行交叉操作 } if ( random ( 0 , 1 ) < Pm ) { 对2个个体按变异概率Pm执行变异操作 } 将2个新个体加入种群newPop中 } until ( M个子代被创建 ) 用newPop取代Pop }until ( 任何染色体得分超过Tf, 或繁殖代数超过G )
四.基本遗传算法优化
下面的方法可优化遗传算法的性能。
精英主义(Elitist Strategy)选择:是基本遗传算法的一种优化。为了防止进化过程中产生的最优解被交叉和变异所破坏,可以将每一代中的最优解原封不动的复制到下一代中。
插入操作:可在3个基本操作的基础上增加一个插入操作。插入操作将染色体中的某个随机的片段移位到另一个随机的位置。
五. 使用AForge.Genetic解决TSP问题
AForge.NET是一个C#实现的面向人工智能、计算机视觉等领域的开源架构。AForge.NET中包含有一个遗传算法的类库。
AForge.NET主页:http://www.aforgenet.com/
AForge.NET代码下载:http://code.google.com/p/aforge/
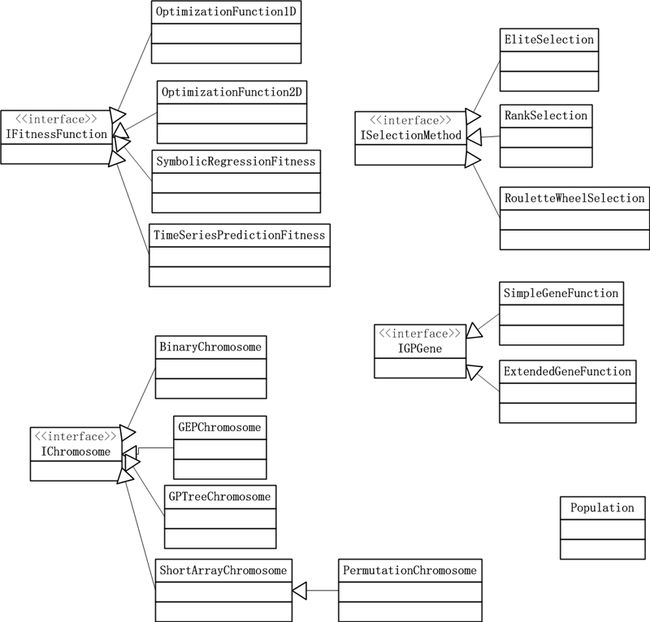
介绍一下AForge的遗传算法用法吧。AForge.Genetic的类结构如下:
图1. AForge.Genetic的类图
下面用AForge.Genetic写个解决TSP问题的最简单实例。测试数据集采用网上流传的中国31个省会城市的坐标:
1304 2312 3639 1315 4177 2244 3712 1399 3488 1535 3326 1556 3238 1229 4196 1004 4312 790 4386 570 3007 1970 2562 1756 2788 1491 2381 1676 1332 695 3715 1678 3918 2179 4061 2370 3780 2212 3676 2578 4029 2838 4263 2931 3429 1908 3507 2367 3394 2643 3439 3201 2935 3240 3140 3550 2545 2357 2778 2826 2370 2975
操作过程:
(1) 下载AForge.NET类库,网址:http://code.google.com/p/aforge/downloads/list
(2) 创建C#空项目GenticTSP。然后在AForge目录下找到AForge.dll和AForge.Genetic.dll,将其拷贝到TestTSP项目的bin/Debug目录下。再通过“Add Reference...”将这两个DLL添加到工程。
(3) 将31个城市坐标数据保存为bin/Debug/Data.txt 。
(4) 添加TSPFitnessFunction.cs,加入如下代码:
using System; using AForge.Genetic; namespace GenticTSP { /// <summary> /// Fitness function for TSP task (Travaling Salasman Problem) /// </summary> public class TSPFitnessFunction : IFitnessFunction { // map private int[,] map = null; // Constructor public TSPFitnessFunction(int[,] map) { this.map = map; } /// <summary> /// Evaluate chromosome - calculates its fitness value /// </summary> public double Evaluate(IChromosome chromosome) { return 1 / (PathLength(chromosome) + 1); } /// <summary> /// Translate genotype to phenotype /// </summary> public object Translate(IChromosome chromosome) { return chromosome.ToString(); } /// <summary> /// Calculate path length represented by the specified chromosome /// </summary> public double PathLength(IChromosome chromosome) { // salesman path ushort[] path = ((PermutationChromosome)chromosome).Value; // check path size if (path.Length != map.GetLength(0)) { throw new ArgumentException("Invalid path specified - not all cities are visited"); } // path length int prev = path[0]; int curr = path[path.Length - 1]; // calculate distance between the last and the first city double dx = map[curr, 0] - map[prev, 0]; double dy = map[curr, 1] - map[prev, 1]; double pathLength = Math.Sqrt(dx * dx + dy * dy); // calculate the path length from the first city to the last for (int i = 1, n = path.Length; i < n; i++) { // get current city curr = path[i]; // calculate distance dx = map[curr, 0] - map[prev, 0]; dy = map[curr, 1] - map[prev, 1]; pathLength += Math.Sqrt(dx * dx + dy * dy); // put current city as previous prev = curr; } return pathLength; } } }
(5) 添加GenticTSP.cs,加入如下代码:
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.IO; using AForge; using AForge.Genetic; namespace GenticTSP { class GenticTSP { static void Main() { StreamReader reader = new StreamReader("Data.txt"); int citiesCount = 31; //城市数 int[,] map = new int[citiesCount, 2]; for (int i = 0; i < citiesCount; i++) { string value = reader.ReadLine(); string[] temp = value.Split(' '); map[i, 0] = int.Parse(temp[0]); //读取城市坐标 map[i, 1] = int.Parse(temp[1]); } // create fitness function TSPFitnessFunction fitnessFunction = new TSPFitnessFunction(map); int populationSize = 1000; //种群最大规模 /* * 0:EliteSelection算法 * 1:RankSelection算法 * 其他:RouletteWheelSelection 算法 * */ int selectionMethod = 0; // create population Population population = new Population(populationSize, new PermutationChromosome(citiesCount), fitnessFunction, (selectionMethod == 0) ? (ISelectionMethod)new EliteSelection() : (selectionMethod == 1) ? (ISelectionMethod)new RankSelection() : (ISelectionMethod)new RouletteWheelSelection() ); // iterations int iter = 1; int iterations = 5000; //迭代最大周期 // loop while (iter < iterations) { // run one epoch of genetic algorithm population.RunEpoch(); // increase current iteration iter++; } System.Console.WriteLine("遍历路径是: {0}", ((PermutationChromosome)population.BestChromosome).ToString()); System.Console.WriteLine("总路程是:{0}", fitnessFunction.PathLength(population.BestChromosome)); System.Console.Read(); } } }
网上据称这组TSP数据的最好的结果是 15404 ,上面的程序我刚才试了几次最好一次算出了15402.341,但是最差的时候也跑出了大于16000的结果。
我这还有一个版本,设置种群规模为1000,迭代5000次可以算出15408.508这个结果。源代码在文章最后可以下载。
总结一下使用AForge.Genetic解决问题的一般步骤:
(1) 定义适应函数类,需要实现IFitnessFunction接口
(2) 选定种群规模、使用的选择算法、染色体种类等参数,创建种群population
(3)设定迭代的最大次数,使用RunEpoch开始计算
本文源代码下载