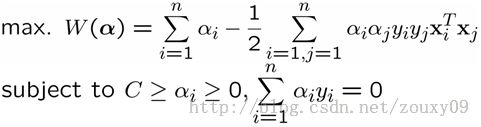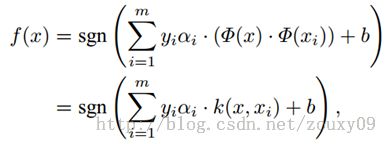机器学习算法与Python实践之（三）支持向量机（SVM）进阶

 机器学习算法与Python实践这个系列主要是参考《机器学习实战》这本书。因为自己想学习Python，然后也想对一些机器学习算法加深下了解，所以就想通过Python来实现几个比较常用的机器学习算法。恰好遇见这本同样定位的书籍，所以就参考这本书的过程来学习了。

       在这一节我们主要是对支持向量机进行系统的回顾，以及通过Python来实现。由于内容很多，所以这里分成三篇博文。第一篇讲SVM初级，第二篇讲进阶，主要是把SVM整条知识链理直，第三篇介绍Python的实现。SVM有很多介绍的非常好的博文，具体可以参考本文列出的参考文献和推荐阅读资料。在本文中，定位在于把集大成于一身的SVM的整体知识链理直，所以不会涉及细节的推导。网上的解说的很好的推导和书籍很多，大家可以进一步参考。

 

目录

一、引入

二、线性可分SVM与硬间隔最大化

三、Dual优化问题

       3.1、对偶问题

       3.2、SVM优化的对偶问题

四、松弛向量与软间隔最大化

五、核函数

六、多类分类之SVM

       6.1、“一对多”的方法

       6.2、“一对一”的方法

七、KKT条件分析

八、SVM的实现之SMO算法

       8.1、坐标下降算法

       8.2、SMO算法原理

       8.3、SMO算法的Python实现

九、参考文献与推荐阅读

 

五、核函数

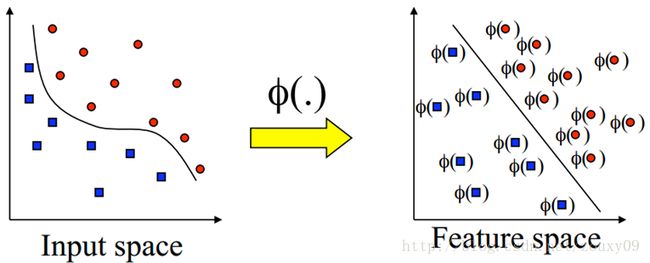
       如果我们的正常的样本分布如下图左边所示，之所以说是正常的指的是，不是上面说的那样由于某些顽固的离群点导致的线性不可分。它是真的线性不可分。样本本身的分布就是这样的，如果也像样本那样，通过松弛变量硬拉一条线性分类边界出来，很明显这条分类面会非常糟糕。那怎么办呢？SVM对线性可分数据有效，对不可分的有何应对良策呢？是核方法（kernel trick）大展身手的时候了。 

       如上图右，如果我们可以把我们的原始样本点通过一个变换，变换到另一个特征空间，在这个特征空间上是线性可分的，那么上面的SVM就可以轻易工作了。也就是说，对于不可分的数据，现在我们要做两个工作：

1）首先使用一个非线性映射Φ(x)将全部原始数据x变换到另一个特征空间，在这个空间中，样本变得线性可分了；

2）然后在特征空间中使用SVM进行学习分类。

       好了，第二个工作没什么好说的，和前面的一样。那第一个粗重活由谁来做呢？我们怎么知道哪个变换才可以将我们的数据映射为线性可分呢？数据维度那么大，我们又看不到。另外，这个变换会不会使第二步的优化变得复杂，计算量更大呢？对于第一个问题，有个著名的cover定理：将复杂的模式分类问题非线性地投射到高维空间将比投射到低维空间更可能是线性可分的。OK，那容易了，我们就要找到一个所有样本映射到更高维的空间的映射。对不起，其实要找到这个映射函数很难。但是，支持向量机并没有直接寻找和计算这种复杂的非线性变换，而是很智慧的通过了一种巧妙的迂回方法来间接实现这种变换。它就是核函数，不仅具备这种超能力，同时又不会增加太多计算量的两全其美的方法。我们可以回头看看上面SVM的优化问题：

      可以看到，对样本x的利用，只是计算第i和第j两个样本的内积就可以了。

       对于分类决策函数，也是计算两个样本的内积。也就是说，训练SVM和使用SVM都用到了样本间的内积，而且只用到内积。那如果我们可以找到一种方法来计算两个样本映射到高维空间后的内积的值就可以了。核函数就是完成这伟大的使命的：

K(x_i, x_j)=Φ(x_i)^T Φ(x_j)

       也就是两个样本x_i和x_j对应的高维空间的内积Φ(x_i)^T Φ(x_j)通过一个核函数K(x_i, x_j)计算得到。而不用知道这个变换Φ(x)是何许人也。而且这个核函数计算很简单，常用的一般是径向基RBF函数：

     这时候，我们的优化的对偶问题就变成了：

      和之前的优化问题唯一的不同只是样本的内积需要用核函数替代而已。优化过程没有任何差别。而决策函数变成了：

        也就是新来的样本x和我们的所有训练样本计算核函数即可。需要注意的是，因为大部分样本的拉格朗日因子α_i都是0，所以其实我们只需要计算少量的训练样本和新来的样本的核函数，然后求和取符号即可完成对新来样本x的分类了。支持向量机的决策过程也可以看做一种相似性比较的过程。首先，输入样本与一系列模板样本进行相似性比较，模板样本就是训练过程决定的支持向量，而采用的相似性度量就是核函数。样本与各支持向量比较后的得分进行加权后求和，权值就是训练时得到的各支持向量的系数α_i和类别标号的成绩。最后根据加权求和值大小来进行决策。而采用不同的核函数，就相当于采用不同的相似度的衡量方法。

       从计算的角度，不管Φ(x)变换的空间维度有多高，甚至是无限维（函数就是无限维的），这个空间的线性支持向量机的求解都可以在原空间通过核函数进行，这样就可以避免了高维空间里的计算，而计算核函数的复杂度和计算原始样本内积的复杂度没有实质性的增加。

       到这里，忍不住要感叹几声。为什么“碰巧”SVM里需要计算的地方数据向量总是以内积的形式出现？为什么“碰巧”存在能简化映射空间中的内积运算的核函数？为什么“碰巧”大部分的样本对决策边界的贡献为0？…该感谢上帝，还是感谢广大和伟大的科研工作者啊！让我等凡夫俗子可以瞥见如此精妙和无与伦比的数学之美！

       到这里，和支持向量机相关的东西就介绍完了。总结一下：支持向量机的基本思想可以概括为，首先通过非线性变换将输入空间变换到一个高维的空间，然后在这个新的空间求最优分类面即最大间隔分类面，而这种非线性变换是通过定义适当的内积核函数来实现的。SVM实际上是根据统计学习理论依照结构风险最小化的原则提出的，要求实现两个目的：1）两类问题能够分开（经验风险最小）2）margin最大化（风险上界最小）既是在保证风险最小的子集中选择经验风险最小的函数。

 

六、多类分类之SVM

       SVM是一种典型的两类分类器，即它只回答属于正类还是负类的问题。而现实中要解决的问题，往往是多类的问题。那如何由两类分类器得到多类分类器呢？

6.1、“一对多”的方法

       One-Against-All这个方法还是比较容易想到的。就是每次仍然解一个两类分类的问题。比如我们5个类别，第一次就把类别1的样本定为正样本，其余2，3，4，5的样本合起来定为负样本，这样得到一个两类分类器，它能够指出一个样本是还是不是第1类的；第二次我们把类别2 的样本定为正样本，把1，3，4，5的样本合起来定为负样本，得到一个分类器，如此下去，我们可以得到5个这样的两类分类器（总是和类别的数目一致）。到了有样本需要分类的时候，我们就拿着这个样本挨个分类器的问：是属于你的么？是属于你的么？哪个分类器点头说是了，文章的类别就确定了。这种方法的好处是每个优化问题的规模比较小，而且分类的时候速度很快（只需要调用5个分类器就知道了结果）。但有时也会出现两种很尴尬的情况，例如拿这个样本问了一圈，每一个分类器都说它是属于它那一类的，或者每一个分类器都说它不是它那一类的，前者叫分类重叠现象，后者叫不可分类现象。分类重叠倒还好办，随便选一个结果都不至于太离谱，或者看看这篇文章到各个超平面的距离，哪个远就判给哪个。不可分类现象就着实难办了，只能把它分给第6个类别了……更要命的是，本来各个类别的样本数目是差不多的，但“其余”的那一类样本数总是要数倍于正类（因为它是除正类以外其他类别的样本之和嘛），这就人为的造成了上一节所说的“数据集偏斜”问题。

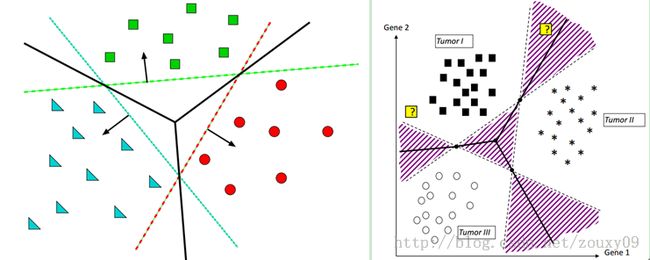
       如下图左。红色分类面将红色与其他两种颜色分开，绿色分类面将绿色与其他两种颜色分开，蓝色分类面将蓝色与其他两种颜色分开。

       在这里的对某个点的分类实际上是通过衡量这个点到三个决策边界的距离，因为到分类面的距离越大，分类越可信嘛。当然了，这个距离是有符号的，如下所示：

       例如下图左，将星星这个点划分给绿色这一类。右图将星星这个点划分给褐色这一类。

6.2、“一对一”的方法

       One-Against-One方法是每次选一个类的样本作正类样本，而负类样本则变成只选一个类（称为“一对一单挑”的方法，哦，不对，没有单挑，就是“一对一”的方法，呵呵），这就避免了偏斜。因此过程就是算出这样一些分类器，第一个只回答“是第1类还是第2类”，第二个只回答“是第1类还是第3类”，第三个只回答“是第1类还是第4类”，如此下去，你也可以马上得出，这样的分类器应该有5 X 4/2=10个（通式是，如果有k个类别，则总的两类分类器数目为k(k-1)/2）。虽然分类器的数目多了，但是在训练阶段（也就是算出这些分类器的分类平面时）所用的总时间却比“一类对其余”方法少很多，在真正用来分类的时候，把一个样本扔给所有分类器，第一个分类器会投票说它是“1”或者“2”，第二个会说它是“1”或者“3”，让每一个都投上自己的一票，最后统计票数，如果类别“1”得票最多，就判这篇文章属于第1类。这种方法显然也会有分类重叠的现象，但不会有不可分类现象，因为总不可能所有类别的票数都是0。如下图右，中间紫色的块，每类的得票数都是1，那就不知道归类给那个类好了，只能随便扔给某个类了（或者衡量这个点到三个决策边界的距离，因为到分类面的距离越大，分类越可信嘛），扔掉了就是你命好，扔错了就不lucky了。

 

七、KKT条件分析

       对KKT条件，请大家参考文献[13][14]。假设我们优化得到的最优解是：α_i*,β_i*, ξ_i*, w*和b*。我们的最优解需要满足KKT条件：

      同时β_i*和ξ_i*都需要大于等于0，而α_i*需要在0和C之间。那可以分三种情况讨论：

       总的来说就是， KKT条件就变成了：

       第一个式子表明如果α_i=0，那么该样本落在两条间隔线外。第二个式子表明如果α_i=C，那么该样本有可能落在两条间隔线内部，也有可能落在两条间隔线上面，主要看对应的松弛变量的取值是等于0还是大于0，第三个式子表明如果0<α_i<C，那么该样本一定落在分隔线上（这点很重要，b就是拿这些落在分隔线上的点来求的，因为在分割线上w^Tx+b=1或者-1嘛，才是等式，在其他地方，都是不等式，求解不了b）。具体形象化的表示如下：

       通过KKT条件可知，α_i不等于0的都是支持向量，它有可能落在分隔线上，也有可能落在两条分隔线内部。KKT条件是非常重要的，在SMO也就是SVM的其中一个实现算法中，我们可以看到它的重要应用。

在之前我们介绍了如何用 Kernel 方法来将线性 SVM 进行推广以使其能够处理非线性的情况，那里用到的方法就是通过一个非线性映射  ϕ(⋅)  将原始数据进行映射，使得原来的非线性问题在映射之后的空间中变成线性的问题。然后我们利用核函数来简化计算，使得这样的方法在实际中变得可行。不过，从线性到非线性的推广我们并没有把 SVM 的式子从头推导一遍，而只是直接把最终得到的分类函数

f(x)=∑i=1nαiyi⟨xi,x⟩+b

中的内积换成了映射后的空间中的内积，并进一步带入了核函数进行计算。如果映射过后的空间是有限维的，那么这样的做法是可行的，因为之前的推导过程会一模一样，只是特征空间的维度变化了而已，相当于做了一些预处理。但是如果映射后的空间是无限维的，还能不能这么做呢？答案当然是能，因为我们已经在这么做了嘛！  但是理由却并不是理所当然的，从有限到无限的推广许多地方都可以“直观地”类比，但是这样的直观性仍然需要严格的数学背景来支持，否则就会在一些微妙的地方出现一些奇怪的“悖论”（例如比较经典的芝诺的那些悖论）。当然这是一个很大的坑，没法填，所以这次我们只是来浮光掠影地看一看核方法背后的故事。

回忆一下原来我们做的非线性映射  ϕ  ，它将原始特征空间中的数据点映射到另一个高维空间中，之前我们没有提过，其实这个高维空间在这里有一个华丽的名字——“再生核希尔伯特空间 (Reproducing Kernel Hilbert Space, RKHS)”。“再生核”就是指的我们用于计算内积的核函数，再说“再生”之前，我们先来简单地介绍一下 Hilbert Space ，它其实是欧氏空间的一个推广。首先从基本的向量空间开始，空间中的点具有加法和数乘的操作，在这个向量空间上定义一个内积操作，于是空间将升级为内积空间。根据内积可以定义一个范数：

∥x∥2=⟨x,x⟩

从而成为一个赋范向量空间。范数可以用于定义一个度量

d(x1,x2)=∥x1−x2∥

从而成为一个度量空间。如果这样的空间在这个度量下是完备的，那么这个空间叫做 Hilbert Space 。简单地来说，Hilbert Space 就是完备的内积空间。最简单的例子就是欧氏空间  Rm  ，这是一个  m  维的 Hilbert Space ，无穷维的例子比如是区间  [a,b]  上的连续函数所组成的空间，并使用如下的内积定义

⟨f1,f2⟩=∫baf1(t)f2(t)dt

我们这里的 RKHS 就是一个函数空间。实际上，在这里我们有一个很有用的性质，就是维度相同的 Hilbert Space 是互相同构的——也就是说空间的各种结构（包括内积、范数、度量和向量运算等）都可以在不同的空间之间转换的时候得到保持。有了这样的性质，就可以让我们不用去关心 RKHS 中的点到底是什么。

将映射记为  ϕ:X→H  ，这里  H  表示 RKHS，用  f  表示里面的元素 ；而  X  是原始特征空间，这里我们甚至不需要要求原始空间必须要是一个欧氏空间或者向量空间（这也是核方法的优点之一），用  x  表示里面的点。由于刚才说了  H  中点的本质是什么对于我们的计算不会产生影响，所以我们可以人为地认为这些点“是什么”——更确切地说，我们认为（或者说定义）  H  中的点是定义在  X  上的函数，在一定的条件下（详见 N. Aronszajn, Theory of Reproducing Kernels），我们可以找到对应于这个 Hilbert Space 的一个（唯一的）再生核函数（Reproducing Kernel）  K:X×X→R  （这里只考虑实函数），满足如下两条性质：

1. 对于任意固定的  x0∈X  ， K(x,x0)  作为  x  的函数属于我们的函数空间  H  。
2. 对于任意  x∈X  和  f(⋅)∈H  ，我们有  f(x)=⟨f(⋅),K(⋅,x)⟩  。

其中第二条性质就叫做 reproducing property ，也是“再生核”名字的来源。至于字面上为什么这么叫，我也不清楚。也许是说元素  x  经过 kernel 映射之后，由内积一乘，又给冒出来了 -.-bb 。有了这个 kernel 之后，我们可以很自然地把映射  ϕ  定义为：

ϕ(x)=K(⋅,x)

由核的再生性质，我们之前的用于计算  H  中内积的 kernel trick 也自然成立了：

⟨ϕ(x1),ϕ(x2)⟩=⟨K(⋅,x1),K(⋅,x2)⟩=K(x1,x2)

再生核有很多很好的性质，比如正定性（在线性代数里这样的性质通常称为“半正定”），也就是说对任意  x1,…,xn∈X  和  ξ1,…,ξn∈R  ，都有

∑i,j=1nK(xi,xj)ξiξj≥0

这是很好证明的，按照核函数的再生性质写成刚才的内积形式，然后把系数拿到内积里面去，上面那个式子就等于  ∥∑ni=1ξiK(⋅,xi)∥2  ，根据范数的性质，也就非负了。

到这里，铺垫已经够多了，于是让我们回到 SVM ，这次我们不是直接偷工减料在最终得到的分类函数上做手脚，而是回到线性 SVM 的最初推导。当然，第一步我们要用刚才定义的映射  ϕ  将数据从原始空间  X  映射到 RKHS  H  中，简单起见，我们用  fi(⋅)  来表示  K(⋅,xi) 。

和以前一样，我们使用一个线性超平面来分隔两类不同的点，并且我们假设经过非线性映射到  H  中之后数据已经是线性可分的了。这个线性超平面由一个线性函数来表示。这里需要再明确一下线性函数的概念，简单的说，如果  x1 、 x2  是向量， α1 、 α2  是标量，那么线性函数应该满足

F(α1x1+α2x2)=α1F(x1)+α2F(x2)

在这里，由于我们讨论的空间  H  中的元素本身就是函数，因此我们把  H  上的函数改称“泛函 (functional)”。根据 Riesz Representation 定理，Hilbert Space 中的任意一个线性泛函  F  ，都有一个  fF∈H  ，使得

F(f)=⟨f,fF⟩,∀f∈H

换句话说，线性函数可以由向量内积表示，这和我们熟知的有限维欧氏空间中是一样的。只是要表示超平面还得再加上一个截距  b

F(f)=⟨f,g⟩+b

这个样子的函数（泛函）严格来说称作仿射函数（泛函）。同我们在第一篇中类似，我们可以定义 margin ，得到 geometrical margin 为

γ=y(⟨f,g⟩+b)∥g∥

类似于原来的推导，我们最终会得到一个如下的目标函数

min12∥g∥2s.t.,yi(⟨fi,g⟩+b)≥1,i=1,…,n

形式上和以前一样，只是把  xi  换成了  fi  ， w  换成了  g  ，但是现在我们要求的参数  g  是在 Hilbert Space 中，特别当  H  是无穷维的时候，是没有办法直接使用数值方法来求解的。即使可以转到 dual 优化推导，但是里面涉及到对无穷维向量的求导之类的问题，我还不知道是不是能直接推广。不过幸运的是，我们在这里可以再把问题转化到有限维空间中。

这需要借助一个叫做 Representer Theorem 的定理，该定理说明，上面这个目标函数（还包括很大一类其他的目标函数）的最优解  g∗  可以写成如下的形式：

g∗=∑i=1naifi

换句话说，可以由这  n  个训练数据（有限集）张成。定理的证明是很简单的，记  H0  为  {f1,…,fn}  张成的子空间，其正交补记为  H⊥0  ，则任意的  f∈H  都可以唯一地表示成  f=f0+f⊥0  ，其中  f0∈H0 、 f⊥0∈H⊥0  ，因此

g∗=g∗0+g∗⊥0

由于  g∗⊥0  垂直于  f1,…,fn  ，因此

⟨fi,g∗⟩=⟨fi,g∗0+g∗⊥0⟩=⟨fi,g∗0⟩+0

因此， g∗⊥0  部分的取值对于目标函数中的约束条件并不产生影响，可以任意定。另一方面，考虑目标函数本身，我们有

∥g∗∥2=∥g∗0+g∗⊥0∥2=∥g∗0∥2+∥g∗⊥0∥2

最后一个等式是由于两者相互垂直而得到的（也就是勾股定理的推广啦），得到这个形式之后，再注意到我们是希望最小化  ∥g∗∥2  ，其中  g∗⊥0  是可以任意取值的，而范数  ∥g∗⊥0∥2  又是非负的，所以在最小值的时候我们必定有  ∥g∗⊥0∥2=0  ，从而