LeetCode221:Maximal Square
Given a 2D binary matrix filled with 0's and 1's, find the largest square containing all 1's and return its area.
For example, given the following matrix:
1 0 1 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 1 0Return 4.
Credits:
Special thanks to @Freezen for adding this problem and creating all test cases.
求一个矩阵中全部包含1的最大正方形的面积。
解法一
动态的规划的核心是定义状态和状态转移方程:
设A[i][j]代表到下标为(i,j)的坐标处的全部为1的正方形的边长。
那么上面例子中的矩阵对应的A的矩阵是:
[1 0 1 0 0]
[1 0 1 1 1]
[1 1 1 2 1]
[1 0 0 1 0]
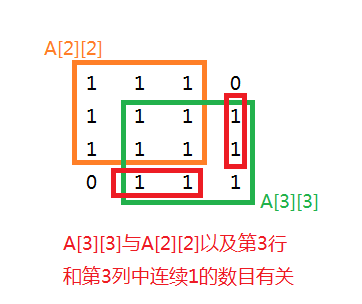
不难发现A[i][j]与A[i-1][j-1]和第i行及j列有关。
A[i][j]与从(i,j)开始第i行A[i-1][j-1]个元素中连续0的个数及从(i,j)开始第j列A[i-1][j-1]个元素中连续0的个数的最小值有关。如下图:
这个分析的方法其实不是很好,因为时间复杂程度是O(M*N*min(M,N)),空间复杂度是O(M*N)。M是矩阵的长度,N是矩阵的宽度。
runtime:16ms
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int height=matrix.size();
if(height==0)
return 0;
int width=matrix[0].size();
vector<vector<int>> vec(height,vector<int>(width,0));
int result=0;
for(int i=0;i<height;i++)
{
for(int j=0;j<width;j++)
{
if(matrix[i][j]=='1')
{
vec[i][j]=1;
if(i-1>=0&&j-1>=0)
{
int size=vec[i-1][j-1];
for(int k=1;k<=size;k++)
{
if(matrix[i-k][j]=='0'||matrix[i][j-k]=='0')
{
size=k-1;
break;
}
}
vec[i][j]+=size;
}
}
result=max(result,vec[i][j]);
}
}
return result*result;
}
};
解法二
然后看Discuss发现上面最里层的循环其实求的有点冤枉,因为A[i][j]表示的就是以(i,j)为右下角的最大的正方形的边长,所以不需要使用for循环,此时状态转移方程就明显很多了,不像解法1还有点模糊,甚至只能用文字描述。
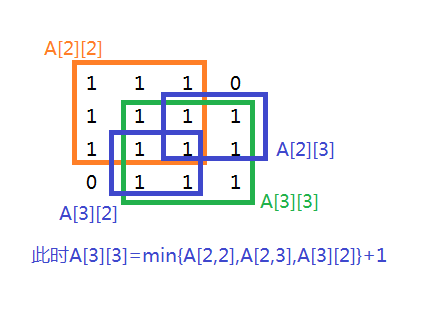
如果matrix[i][j]为1,那么A[i][j]=min(A[i-1][j-1],A[i-1][j],A[i][j-1])+1;如果matrix[i][j]为0,那么A[i][j]为0。
查看这个方程就好理解多了。
如下图:
最大的正方形边长为max{A[i][j]}。
此时时间复杂程度是O(M*N),空间复杂程度是O(M*N)。
runtime:14ms
int maximalSquare(vector<vector<char>>& matrix) {
int height=matrix.size();
if(height==0)
return 0;
int width=matrix[0].size();
vector<vector<int>> vec(height,vector<int>(width,0));
int result=0;
for(int i=0;i<height;i++)
{
for(int j=0;j<width;j++)
{
if(matrix[i][j]=='1')
{
vec[i][j]=1;
if(i>0&&j>0)
vec[i][j]+=min(min(vec[i-1][j],vec[i][j-1]),vec[i-1][j-1]);
}
result=max(result,vec[i][j]);
}
}
return result*result;
}
解法三
然后发现了可以对空间复杂度进行改进的方法:
从上面解法二可以看出A[i][j]只与A[i-1][j],A[i][j-1],A[i-1][j-1]有关,即只与当前一列和上一列有关,所以可以只使用含有两个矩阵宽度长的向量来保存数据即可。这样时间复杂度是O(M*N),空间复杂度是O(N)。
runtime:15ms
int maximalSquare(vector<vector<char>>& matrix) {
int height=matrix.size();
if(height==0)
return 0;
int width=matrix[0].size();
vector<vector<int>> vec(2,vector<int>(width,0));
int result=0;
for(int i=0;i<height;i++)
{
for(int j=0;j<width;j++)
{
vec[i%2][j]=0;//注意这里需要对其进行清空
if(matrix[i][j]=='1')
{
vec[i%2][j]=1;
if(i>0&&j>0)
vec[i%2][j]+=min(min(vec[(i-1)%2][j],vec[i%2][j-1]),vec[(i-1)%2][j-1]);
}
result=max(result,vec[i%2][j]);
}
}
return result*result;
}
LeetCode中的参考的解法:https://leetcode.com/discuss/39403/simple-and-efficient-implementation-using-dp-in-c
https://leetcode.com/discuss/38489/easy-solution-with-detailed-explanations-8ms-time-and-space