二叉树遍历的应用(路径和问题,判断是否是二叉搜索树,判断是否是二叉平衡树)
现在越发觉得关于树的问题真是千变万化,随便改一个条件又会是一个新的问题。
先序遍历求二叉树路径问题
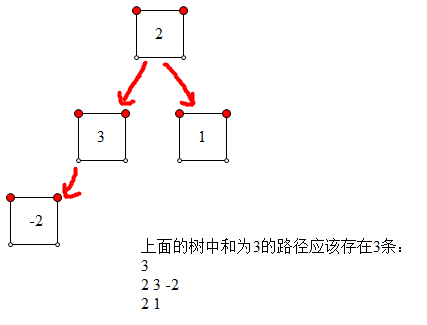
问题:一棵二叉树每个节点包含一个整数,请设计一个算法输出所有满足条件的路径:此路径上所有节点之和等于给定值。注意此类路径不要求必须从根节点开始。
如果没有最后一个条件,这道题在leetcode上面见过,就是采取先序遍历的方式并记录下路径。但是加上最后一个条件后需要转下弯思考一下。
当然也需要记录下路径,并且记得要回溯。加上不要求从根节点开始这个条件后可以这么思考,每次遍历到当前节点时,从路径中查找包含当前节点的符合条件的部分子数组的和为给定的值的路径。
//树节点信息
class TreeNode
{
public:
int data;
TreeNode * left;
TreeNode* right;
TreeNode(int d,TreeNode * l=NULL,TreeNode * r=NULL)
{
data=d;
left=l;
right=r;
}
};
//打印输出数据
void printA(vector<int> vec,int lev1,int lev2)
{
for (int i=lev1;i<=lev2;i++)
{
cout<<vec[i]<<" ";
}
cout<<endl;
}
void findSum(TreeNode * head,int sum,vector<int> &buffer,int level)
{
if (head==NULL)
return ;
int tmp=sum;
//当前节点数据加入缓冲区中
buffer.push_back(head->data);
//注意这个处理方式,这是和从根节点到当前节点和为指定值另外这个问题不同的地方
for (int i=level;i>=0;i--)
{
tmp-=buffer[i];
if (tmp==0)
{
printA(buffer,i,level);
}
}
//访问左子树
findSum(head->left,sum,buffer,level+1);
//访问右子树
findSum(head->right,sum,buffer,level+1);
//注意回溯是发生在左右子树都遍历完后
//回溯是指退出当前节点时该做的处理
buffer.pop_back();
}
上面的findSum方法传递的buffer参数是引用,并且采用的是先序遍历的方式。所以最后一行代码是回溯的处理。如果buffer参数不是引用,那么就不需要进行回溯处理了。
从这两种处理方式中可以加深对回溯的理解。明显上面一种方式效率会比下面的代码效率高很多,但是上面的代码在什么地方回溯以及是否需要回溯需要处理好,下面的代码就不需要考虑这么多了。
void findSum(TreeNode * head,int sum,vector<int> buffer,int level)
{
if (head==NULL)
return ;
int tmp=sum;
//当前节点数据加入缓冲区中
buffer.push_back(head->data);
//注意这个处理方式,这是和从根节点到当前节点和为指定值另外这个问题不同的地方
for (int i=level;i>=0;i--)
{
tmp-=buffer[i];
if (tmp==0)
{
printA(buffer,i,level);
}
}
//访问左子树
findSum(head->left,sum,buffer,level+1);
//访问右子树
findSum(head->right,sum,buffer,level+1);
//注意回溯是发生在左右子树都遍历完后
//回溯是指退出当前节点时该做的处理
//如果buffer不是引用,不需要回溯处理,并且上面访问左右子树中间也不需要添加回溯的代码
//这是因为访问左子树时对buffer的修改不会影响到访问右子树时buffer的内容
// buffer.pop_back();
}
使用下面的测试用例:
int main()
{
TreeNode * t1=new TreeNode(-2);
TreeNode * t2=new TreeNode(3,t1);
TreeNode * t3=new TreeNode(1);
TreeNode * t4=new TreeNode(2,t2,t3);
vector<int> buffer;
findSum(t4,3,buffer,0);
getchar();
return 0;
}
树的形态如下:
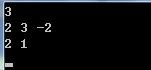
程序输出:
中序遍历判断一棵树是否是二叉排序树
如何判断一棵二叉树是不是排序树?
根据二叉排序树的中序遍历结果是从小到大有序的这个特征来判断树是不是二叉排序树。当然可以使用一个数组记录下路径,然后判断这个数组中的元素是不是排序好的,但是这样会有O(n)的空间开销。有一种方法可以直接在遍历的过程中就进行比较,就是定义一个变量来保存前一个访问的节点的值。
从这个例子中可以学习到如何保存前一个访问的节点的值,可以通过全局变量或引用来实现,我这里使用的是引用,当然全局变量也可以。
//这个例子注意如何保存前一个访问的节点的,是通过引用实现的
//当然也可以通过一个全局变量来实现
bool judgeSorted(TreeNode * root,int & pre)
{
if (root==NULL)
return true;
//判断左子树是不是平衡的
bool left=judgeSorted(root->left,pre);
//如果左子树不是平衡的或者前一个节点的值大于当前节点,那么返回false
if (!left||pre> root->data)
return false;
pre=root->data;//访问完当前节点后需要更新pre的值,这样在遍历右子树时pre就是当前节点
return judgeSorted(root->right,pre);
}
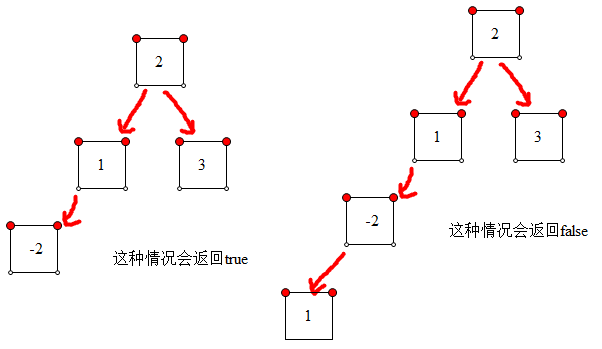
还是使用上面那棵二叉树,可以发现结果返回false,如果将上面节点3和1交换,那么结果返回的是true。
后序遍历判断一棵树是否是平衡二叉树
判断一棵树是不是平衡二叉树?
判断一棵树是不是平衡二叉树可以采用先序遍历,每遍历到一个节点,计算它的左右子树的深度,比较它们的深度差,如果深度差小于1,那么分别遍历左子树和右子树,这样一直递归下去,但这种方法效率很低,因为存在大量的重复。
使用后序遍历就可以避免上面的重复问题了,采用后序遍历遍历二叉树时每遍历到一个节点之前已经遍历了它的左右子树了,只要遍历到每一个节点时记录下它的高度,就可以避免上面先序遍历时大量的重复操作了。
//采用后序遍历的方式遍历二叉树
bool isBalance(TreeNode * root,int &depth)
{
if (root==NULL)
{
depth=0;
return true;
}
int left,right;
//先访问左子树,再访问右子树
if (isBalance(root->left,left)&&isBalance(root->right,right))
{
//如果左右子树都是平衡的,那么需要比较左右子树的高度差,如果高度差小于1,那么说明
//遍历到当前节点时这个以这个节点为根节点的子树是平衡的
int diff=left-right;
if (diff>=-1&&diff<=1)
{
depth=max(left,right)+1;
return true;
}
}
return false;
}
最后还有一种更巧妙的方法来求解上面的问题,可以找到离根节点深度最小的节点和深度最大的节点,根据这两个深度的差值来判断这棵树是不是二叉平衡树:
感觉这种解法最巧妙,但是很难想到。
//求距离root最远的点的深度
int maxHeight(TreeNode * root)
{
if (root==NULL)
return 0;
return max(maxHeight(root->left),maxHeight(root->right))+1;
}
//求距离root最近的节点的深度
int minHeight(TreeNode * root)
{
if (root==NULL)
return 0;
return min(minHeight(root->left),minHeight(root->right))+1;
}
bool isBalance(TreeNode * root)
{
int diff=maxHeight(root)-minHeight(root);
return diff>=-1&&diff<=1;
}