凸包——Graham-Scan算法

Graham-Scan算法是一种灵活的凸包算法，时间复杂度是O(nlogn)

算法细节：

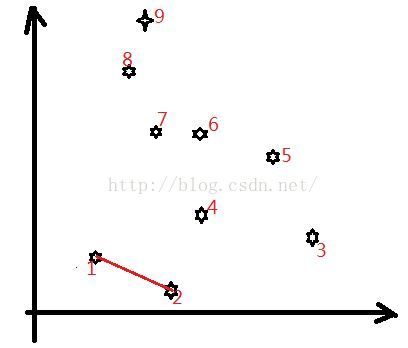
1. 选出最左下角的点（排序：x最小，其次是y最小）

2. 其余点按极角排序，在极角相等的情况下距离极点(p[0])最近的优先

3. 用一个栈（数组）存储凸包上的点，先把p[0],p[1]压入栈。

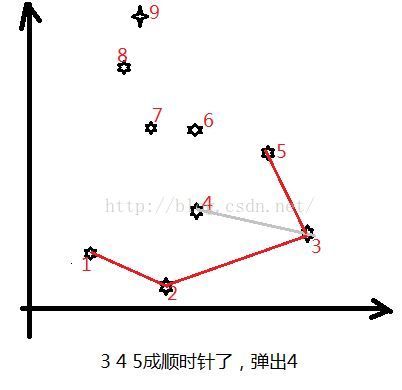
4. 扫描每一个点，用叉积判断新点和栈顶头两个点形成的拐向。顺时针就弹出栈顶元素，继续判断。否则压入新点p[i]

（判断的前提是栈内已经压入了两个点）

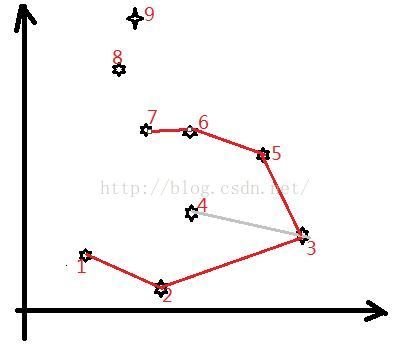
5. 最终栈内元素就是凸包点。

附图说明（接下来看图，用心感受）：

还是那一道凸包入门题，之前用卷包裹法做过：http://blog.csdn.net/thearcticocean/article/details/50421206

现在用Graha-Scan算法做，更加高效：

POJ 1113 Wall

poj.org/problem?id=1113

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;
const double eps=1e-7,Pi=3.1415926;
struct point{
    int x,y;
}p[1005],ans[1005];

int cross(point p0,point p1,point p2){
    return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}

double dis(point a,point b){
    return sqrt(1.0*(a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}

int cmp1(point p1,point p2){
    return p1.x<p2.x||(p1.x==p2.x&&p1.y<p2.y);
}

int cmp2(point p1,point p2){
    int c1=cross(p[0],p1,p2);  //tp,p1),c2=cross(p[0],tp,p2);
    if(c1==0){
        return dis(p1,p[0])<dis(p2,p[0]);
    }
    return c1>0;
}

int top;
void convex(int n){
    top=0;
    sort(p,p+n,cmp1);
    sort(p+1,p+n,cmp2);
    ans[top++]=p[0];
    ans[top++]=p[1];
    for(int i=2;i<n;i++){
        if(cross(ans[top-2],ans[top-1],p[i])>0) ans[top++]=p[i];
        else {
            top--;  
            while(top>=2&&cross(ans[top-2],ans[top-1],p[i])<=0) top--;
            ans[top++]=p[i];
        }
    }
    ans[top++]=p[0];
}
int main()
{
    //freopen("cin.txt","r",stdin);
    int n,l;
    while(cin>>n>>l){
        for(int i=0;i<n;i++){
            scanf("%d%d",&p[i].x,&p[i].y);
        }
        convex(n);
        double sum=0;
        for(int i=0;i<top-1;i++){
            sum=sum+dis(ans[i],ans[i+1]); // this is ans[] , not p[], fucos on your var
        }
        sum=sum+2*Pi*l;
        printf("%d\n",int(sum+0.5));
    }
    return 0;
}