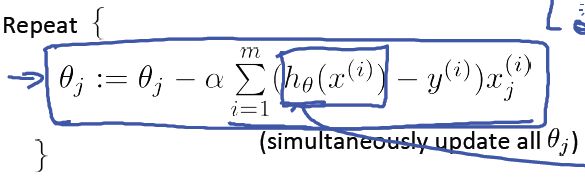梯度下降原理及在线性回归、逻辑回归中的应用

1 基本概念

1）定义

梯度下降法，就是利用负梯度方向来决定每次迭代的新的搜索方向，使得每次迭代能使待优化的目标函数逐步减小。

梯度下降法是2范数下的最速下降法。 最速下降法的一种简单形式是：x(k+1)=x(k)-a*g(k),其中a称为学习速率，可以是较小的常数。g（k）是x(k)的梯度。

梯度其实就是函数的偏导数。

2）举例

对于函数z=f(x,y)，先对x求偏导，再对y求偏导，则梯度为(,)。

比如，偏导=4x,=6y。则在(2,4)点的梯度(8,24)。

2 梯度下降在线性回归中的应用

假定函数为如下形式：

cost function采用最小均方损失函数：

这个错误估计函数是对x(i)的估计值与真实值y(i)差的平方和（梯度下降要考虑所有样本）作为错误估计函数，前面乘上的1/2是为了在求导的时候，这个系数就不见了。

我们的目标是选择合适的，使得cost function的值最小。

接下来介绍梯度减少的过程，即对函数求偏导。因为是线性函数，对每个分量\theta _{i}求编导的时候，其它项为0。

更新的过程，也就是θi会向着梯度最小的方向进行减少。θi表示更新之前的值，-后面的部分表示按梯度方向减少的量，α表示步长，也就是每次按照梯度减少的方向变化多少。

 一个很重要的地方值得注意的是，梯度是有方向的，对于一个向量θ，每一维分量θi都可以求出一个梯度的方向，我们就可以找到一个整体的方向，在变化的时候，我们就朝着下降最多的方向进行变化就可以达到一个最小点，不管它是局部的还是全局的。

3 梯度下降在逻辑回归中的应用

对数损失函数：

由于y 只能等于0或1，所以可以将逻辑回归中的Cost function的两个公式合并，具体推导如下：

故逻辑回归的Cost function可简化为：

注意中括号中的公式正是对逻辑回归进行最大似然估计中的最大似然函数，对于最大似然函数求最大值，从而得到参数(\theta\)的估计值。反过来，这里为了求一个合适的参数，需要最小化Cost function，也就是：

minθJ(θ)

而对于新的变量x来说，就是根据 hθ(x) 的公式输出结果：

与线性回归相似，这里我们采用梯度下降算法来学习参数 θ ，对于 J(θ) :

目标是最小化 J(θ) ，则梯度下降算法的如下：

对 J(θ) 求导后，梯度下降算法如下：

注意，这个算法和线性回归里的梯度下降算法几乎是一致的，除了 hθ(x) 的表示不同。

4 参考文献：

梯度下降算法，http://blog.sina.com.cn/s/blog_62339a2401015jyq.html

梯度下降法，http://deepfuture.iteye.com/blog/1593259

斯坦福大学机器学习第六课“逻辑回归，http://52opencourse.com/125/coursera%E5%85%AC%E5%BC%80%E8%AF%BE%E7%AC%94%E8%AE%B0-%E6%96%AF%E5%9D%A6%E7%A6%8F%E5%A4%A7%E5%AD%A6%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0%E7%AC%AC%E5%85%AD%E8%AF%BE-%E9%80%BB%E8%BE%91%E5%9B%9E%E5%BD%92-logistic-regression

BP算法浅谈，http://blog.csdn.net/pennyliang/article/details/6695355

5 收获

1）了解了梯度的概念；

2） 复习了导数公式、偏导数的概念；

3）对梯度下降公式进行了推导，掌握更牢固。