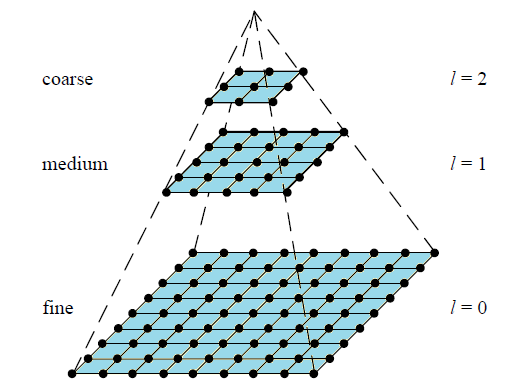
图像的多分辨率金字塔详解

高斯核的产生：

函数 kron
格式 C=kron (A,B)    %A为m×n矩阵，B为p×q矩阵，则C为mp×nq矩阵。

kron即为Kronecker积，所谓Kronecker积是一种矩阵运算，其定义可以简单描述成：
X与Y的Kronecker积的结果是一个矩阵：
X11*Y   X12*Y … X1n*Y
X21*Y   X22*Y … X2n*Y
……
Xm1*Y   Xm2*Y … Xmn*Y

例如：

高斯核的生成：

<span style="font-size:18px;">cw = .375; 
ker1d = [.25-cw/2 .25 cw .25 .25-cw/2];
kernel = kron(ker1d,ker1d');</span>

多分辨率金字塔 的产生主要下面的步骤：

1、对图像进行高斯平滑

2、对高斯滤波后的图像进行降采样或者上采样

（1）. 高斯核是唯一可以产生多尺度空间的核；

一幅图像的尺度空间 L(x, y, σ), 定义为原始图像 I(x,y) 与一个可变尺度的2维高斯函数G(x, y, σ)卷积运算。

即尺度空间形式表示为：

其中，

（2）（金字塔）多分辨率表达——降采样

图像金字塔化一般包括两个步骤：使用低通滤波器平滑图像；对图像进行降采样（通常是水平，竖直方向1/2），从而得到一系列尺寸缩小的图像。对于二维图像，每一层图像由上一层分辨率的长、宽各一半，也就是四分之一的像素组成。

<span style="font-size:18px;">实验代码详解：</span>

<span style="font-size:18px;">
</span>

<span style="font-size:18px;">%读入图像并将其转换成灰度图像 
I=imread('tiantan.jpg');
I=rgb2gray(I);
% 生成高斯滤波器的核 
w=fspecial('gaussian',3,0.5);
size_a=size(I);

% 进行高斯滤波
g=imfilter(I,w,'conv','symmetric','same');

% 降采样 
t=g(1:2:size_a(1),1:2:size_a(2));

% 显示处理结果
imshow(I);
figure
imshow(t)</span>

<span style="font-size:18px;">
</span>

<span style="font-size:18px;">上采样函数代码</span>

<span style="font-size:18px;"></span><pre name="code" class="html">% 调用金子塔类
hgausspymd = video.Pyramid;
% 设定金字塔分解的层数为2
hgausspymd.PyramidLevel = 2;
% 读入图像
x = imread('qingdao.jpg');
% 执行金字塔分解
y = step(video.Pyramid, x);
% 显示结果
figure, imshow(x); title('原始图像');
x1=mat2gray(double(y));
figure, imshow(x1);
title('Decomposed Image');