经典回溯算法之N皇后问题
背景问题:http://acm.hdu.edu.cn/showproblem.php?pid=2553
在N*N的方格棋盘放置了N个皇后,使得它们不相互攻击(即任意2个皇后不允许处在同一排,同一列,也不允许处在与棋盘边框成45角的斜线上。
你的任务是,对于给定的N,求出有多少种合法的放置方法。
分析:
最单纯的思路:枚举最坏的情况是 10重长度是10的循环即10^10,如果用有与没有的思路考虑将达到可怕的2^100
最单纯的思路:枚举最坏的情况是 10重长度是10的循环即10^10,如果用有与没有的思路考虑将达到可怕的2^100
学习了神奇的递归回溯,发现它可以有更优的解法:
以N=4为例说明整个回溯查找过程:
void show(int a){
bitset<10> ba(a);
cout<<ba<<" ";
}
void dfs(int col,int left,int right){
show(((~(col|left|right))&full)); show(col); show(left); show(right); cout<<endl;
if(col==full){ ans++; cout<<ans<<endl; return ; }
int can=(~(col|left|right))&full;
while(can){
int lowbit=can&(can^(can-1));
dfs(lowbit|col,(lowbit|left)>>1,(lowbit|right)<<1&full);
can=can&(~lowbit);
}
}
中间数据(第一列数字1代表当前行能放的位置列,第二,三,四列所有1代表当前行不能放的列,3者分别对应上一行放下的棋子影响的列、影响的左对角线,右对角线。数据是从棋盘的上一行推导下一行,利用回溯实现修改点):
4
0000001111 0000000000 0000000000 0000000000
0000001100 0000000001 0000000000 0000000010
0000000000 0000000101 0000000010 0000001100
0000000010 0000001001 0000000100 0000000100
0000000000 0000001011 0000000011 0000001100
0000001000 0000000010 0000000001 0000000100
0000000001 0000001010 0000000100 0000001000
0000000100 0000001011 0000000010 0000000010
0000000000 0000001111 0000000011 0000001100
1
0000000001 0000000100 0000000010 0000001000
0000001000 0000000101 0000000001 0000000010
0000000010 0000001101 0000000100 0000000100
0000000000 0000001111 0000000011 0000001100
2
0000000011 0000001000 0000000100 0000000000
0000000100 0000001001 0000000010 0000000010
0000000000 0000001101 0000000011 0000001100
0000000000 0000001010 0000000011 0000000100
2
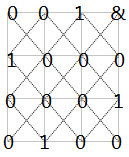
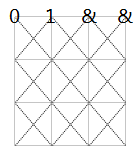
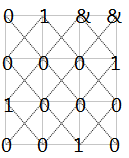
图文说明:
1代表放置皇后棋子:
第3行不能放棋子了,回溯。
&表示已经遍历过了的。
此时,第4行不能放棋子了。再次回溯,直至最顶层,得到上图。
此时最后一行只有一个位置能放棋子。
整个棋盘已经放置完毕。这是1种放置棋子的方式
接下来就是回溯算法发挥威力的时候了。
回溯至最顶层,接着找另一种方法的起始位置:
重复第一种的试探法,放满整个棋盘:
第二种方法就这样找到了。
接着回溯试探性的寻找第三种方法:
结果发现这是不存在的。
所以最终的结果就是2.
那个背景问题的代码:
那个背景问题的代码:
#include <iostream>
#include <cstdio>
using namespace std;
int full,ans;
void dfs(int col,int left,int right){
if(col==full){ ans++; return ; }
int can=(~(col|left|right))&full;
while(can){
int lowbit=can&(can^(can-1));
dfs(lowbit|col,(lowbit|left)>>1,(lowbit|right)<<1&full);
can=can&(~lowbit);
}
}
int main()
{
int n;
while(cin>>n&&n){
full=(1<<n)-1;
ans=0;
dfs(0,0,0);
printf("%d\n",ans);
}
return 0;
}