数据结构--树和二叉树

1.       树的一些基本概念

结点的度：每个节点下面有几个。

树的度：最多的结点的度。

叶子结点：0个度

分支结点：除了叶子结点都为分支结点

内部结点：中间的结点，不是最底层也不是最高层。

父结点：相对来说，不能单独来说

子结点：相对来说，不能单独来说

兄弟结点：同一层的结点

结点=度+1

2.       树的遍历

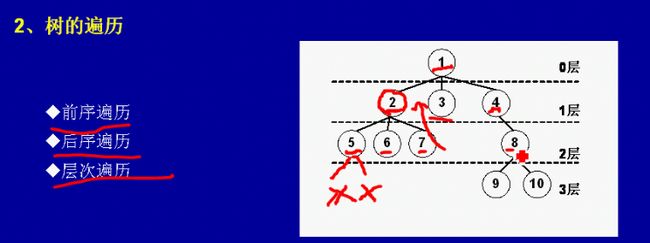
树的遍历分为前序遍历，后序遍历和层次遍历。

 

前序遍历：1,2,5,6,7,3,4,8,9,10

后序遍历：5,6,7,2,3,9,10,8,4,1

层次遍历：1,2,3,4,5,6,7,8,9,10

 

3.       二叉树的一些相关概念和特性

二叉树的一些特性：

1.      在二叉树的第i层上最多有2^i-1个结点。

2.      深度为k的二叉树最多为2^k-1个结点。

3.      对任何一棵二叉树，如果其叶子结点数为n₀，度为2的节点数为n₂，则n₀=n₂+1

4.      具有n（n>0）个结点的完全二叉树的深度为  向上取整log₂n+ 1

5.      如果对一棵有n个结点的完全二叉树的结点按层序编号（从第1层到第向上取整log2n + 1，每层从左到右），则对任一结点i（1≤i≤n），有

（1）      如果i=1，则结点i无双亲，是二叉树的根；如果i>1，则其双亲是结点向上取整i/2。

（2）      如果2i>n，则结点i为叶子结点，无左孩子；否则，其左孩子是结点2i。

（3）      如果2i+1>n，则结点i无右孩子；否则，其右孩子是结点2i+1.

4.       二叉树的遍历

由于二叉树自身的特点，遍历多了一种中序遍历。

         前序遍历：根左右的顺序。

中序遍历：左根右的顺序。

后序遍历：左右根的顺序。

5.       树与二叉树的转换

转换之后前序遍历不会变，中序遍历和后续遍历是一样的。

6.       查找二叉树（二叉排序树）的基本定义、查找二叉树的基本操作

空二叉树也是查找二叉树。

性质：

1.      若左子树非空，则左子树上所有结点的值均小于根节点；

2.      若右子树非空，则右子树上所有结点的值均大于根节点。

3.      左右子树本山又各是一棵二叉排序树。

 

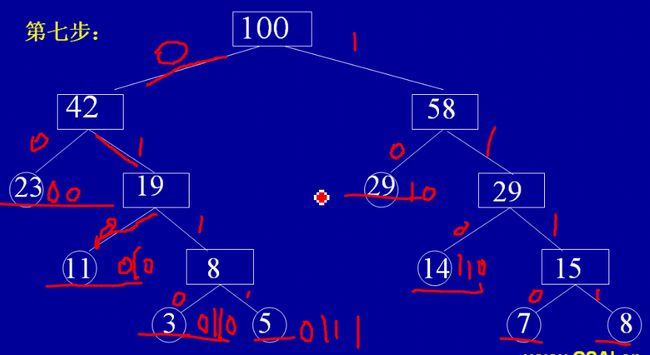
7.       最优二叉树（哈夫曼树）

树的路径长度（相同结点的树完全二叉树的路径最短）

权：某个结点的具体值

带权路径长度：具体值*路径长度（叶子结点）（频度）

树的带权路径长度（树的代价）：所有的带权路径长度都加起来

哈夫曼树：就是带权路径长度最短的树。

 

哈夫曼编码：

 

8.       线索二叉树

把结点的空的指针用来存放前驱结点和后继结点的信息。

 

9.       平衡二叉树

一棵空树，或者任一结点的左右子树的深度相差不超过1.