SPOJ 694、705 后缀数组：求不同子串

思路：这题和wikioi 1306一样，也都是求的不同子串的个数，但是wikioi 时间比较长，然后用Trie树就过了。但是我用那个代码提交这题的时候就WA了，比较晕……因为这题有多组样例，所以超了点时间。

所以这题当然就是用后缀数组做的啦！

算法分析：

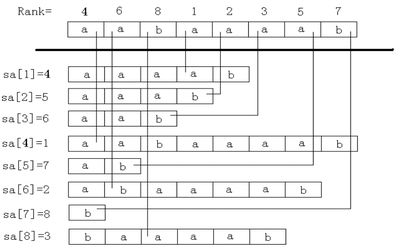
每个子串一定是某个后缀的前缀，那么原问题等价于求所有后缀之间的不相同的前缀的个数。如果所有的后缀按照suffix(sa[1]),suffix(sa[2]),suffix(sa[3]),……,suffix(sa[n])的顺序计算，不难发现，对于每一次新加进来的后缀suffix(sa[k]),它将产生n-sa[k]+1个新的前缀。但是其中有height[k]个是和前面的字符串的前缀是相同的。所以suffix(sa[k])将“贡献”出n-sa[k]+1-height[k]个不同的子串。累加后便是原问题的答案。这个做法的时间复杂度为O(n)。

看下面这个图就比较好理解为什么是n-sa[k]+1-height了，因为有多少个字符，当然就有多少个前缀咯，也就是子串咯，而不同的把相同的前缀减去就行了：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
#include<queue>
#include<set>
#include<cmath>
#include<bitset>
#define mem(a,b) memset(a,b,sizeof(a))
#define lson i<<1,l,mid
#define rson i<<1|1,mid+1,r
#define llson j<<1,l,mid
#define rrson j<<1|1,mid+1,r
#define INF 0x7fffffff
#define maxn 100010
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
void radix(int *str,int *a,int *b,int n,int m)
{
    static int count[maxn];
    mem(count,0);
    for(int i=0;i<n;i++) ++count[str[a[i]]];
    for(int i=1;i<=m;i++) count[i]+=count[i-1];
    for(int i=n-1;i>=0;i--) b[--count[str[a[i]]]]=a[i];
}
void suffix(int *str,int *sa,int n,int m) //倍增算法计算出后缀数组sa
{
    static int rank[maxn],a[maxn],b[maxn];
    for(int i=0;i<n;i++) rank[i]=i;
    radix(str,rank,sa,n,m);
    rank[sa[0]]=0;
    for(int i=1;i<n;i++)
        rank[sa[i]]=rank[sa[i-1]]+(str[sa[i]]!=str[sa[i-1]]);
    for(int i=0;1<<i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            a[j]=rank[j]+1;
            b[j]=j+(1<<i)>=n?0:rank[j+(1<<i)]+1;
            sa[j]=j;
        }
        radix(b,sa,rank,n,n);
        radix(a,rank,sa,n,n);
        rank[sa[0]]=0;
        for(int j=1;j<n;j++)
            rank[sa[j]]=rank[sa[j-1]]+(a[sa[j-1]]!=a[sa[j]]||b[sa[j-1]]!=b[sa[j]]);
    }
}
void calcHeight(int *str,int *sa,int *h,int n) //求出最长公共前缀数组h
{
    static int rank[maxn];
    int k=0;
    h[0]=0;
    for(int i=0;i<n;i++) rank[sa[i]]=i;
    for(int i=0;i<n;i++)
    {
        k=k==0?0:k-1;
        if(rank[i])
            while(str[i+k]==str[sa[rank[i]-1]+k]) k++;
        else k=0;
        h[rank[i]]=k;
    }
}
int a[maxn],sa[maxn],height[maxn];
int main()
{
    //freopen("test.txt","r",stdin);
    int t;
    scanf("%d",&t);
    while(t--)
    {
        char s[50005];
        scanf("%s",s);
        int n=strlen(s);
        copy(s,s+n,a);
        suffix(a,sa,n,256);
        calcHeight(a,sa,height,n);
        //for(int i=0;i<n;i++)
        //    cout<<height[i]<<' '<<sa[i]<<endl;
        int sum=n-sa[0];//刚开始没有从0算，然后少了一个
        for(int i=1;i<n;i++) //刚开始从2到n了直WA
            sum+=n-sa[i]-height[i];
        printf("%d\n",sum);
    }
    return 0;
}