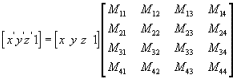矩阵与变换
Direct3D中使用矩阵(matrices)来定义世界(world), 视(view)和投影变换(projection transformation)。如果你以前没有编制过三维图形程序,那么这一部分将向你介绍有关的主要内容。如果你已经对三维图形程序比较熟悉,那么可以跳过这一部分。
- 矩阵(Matrices)
- 3-D变换(3-D Transformations)
1. 矩阵
尽管我们不需要对线性代数有非常深入的了解,但是在进行矩阵运算时,我们还是应该对它的内容比较熟悉才行。要相对一些基本的内容再复习以下的话,请看“三维变换(3-D Transformations)”。
Direct3D种的矩阵由D3DMATRIX结构来定义,并且是4×4的。
D3DMATRIX结构中的D3D_OVERLOADS工具(D3DMATRIX (D3D_OVERLOADS))执行一个圆括号操作符("()")。这个操作符可以在C++程序中提供对矩阵中数据的访问。C++程序员不需要通过它们的名称来查询结构体成员,而可以通过行列号查询它们,或者简单的将这些序号编入索引。这些索引是由0开始的,例如,一个元素位于第三行、第二列,那么它就应该表示为M(2, 1)。要使用D3D_OVERLOADS操作符,不许在包含D3dtypes.h头文件之前对D3D_OVERLOADS进行定义。
另外,D3dutil.cpp源文件提供了一些辅助函数(helper function)来创建和连接矩阵。这些函数可以自由使用,也可以做你自己编制的矩阵操作函数的一部分来使用。
执行缓冲(Execute buffer)注意事项:在使用执行缓冲时,矩阵只会以句柄(handle)的形式出现。这些句柄(有D3DMATRIXHANDLE类型定义)被用于D3DOP_MATRIXLOAD和D3DOP_MATRIXMULTIPLY执行缓冲操作码(opcodes)中。
你可以通过调用IDirect3DDevice::CreateMatrix方法来创建一个Direct3D矩阵,调用IDirect3DDevice::SetMatrix方法来设置矩阵的内容。
2. 三维变换
Direct3D使用矩阵来执行3-D变换。这一部分解释了矩阵是如何来建立三维变换,描述了一些变换的基本用法,以及如何通过矩阵合并来完成复杂的变换。我们分以下几个部分来讨论:
- 关于三维变换About 3-D Transformations
- 平移Translation
- 旋转Rotation
- 缩放Scaling
- 矩阵级联Matrix Concatenation
注:有关Direct3D立即模式中变换的更多内容见“几何管道Geometry Pipeline”部分。
2.1 关于三维变换
在三维图形程序中,我们可以用几何变换来达到以下目的:
- 表示一个对象相对于另一个对象的位置。
- 旋转和安排对象的大小。
- 改变视维、方向和透视方法。
你可以使用一个4×4的矩阵将任何点变换到另一个点。下面的例子中,我们用一个矩阵对点(x, y, z)进行变化,产生了一个新的点(x', y', z'):
对点(x, y, z)进行一下运算,会得到一个新点(x', y', z'):
最常用的变换包括:平移(translation),旋转(rotation)和缩放(scaling)。你可以将这些变换合并起来,组成一个矩阵,同时进行几种变换。
矩阵以行列号的形式来描述。沿每个坐标轴同时进行缩放时(我们称为统一缩放uniform scaling),矩阵如下所示:
Direct3D立即模式中的矩阵被描述为一个二维数组,它要用到D3DMATRIX结构体。下面的例子展示了如何通过初始化D3DMATRIX结构来得到一个统一缩放矩阵:
|
2.2 平移
下面的变化将一个点(x, y, z)平移到另一个点(x', y', z'):
你可以自己来创建一个平移矩阵,也可以使用D3dutil.cpp文件中的Translate辅助函数来创建此矩阵。下面的例子展示了Translate函数的源码:
| D3DMATRIX Translate(const float dx, const float dy, const float dz) { D3DMATRIX ret = IdentityMatrix(); ret(3, 0) = dx; ret(3, 1) = dy; ret(3, 2) = dz; return ret; } // end of Translate() |
2.3 旋转
这里我们用的变化都是在左手坐标下进行的,它可能与你在其它地方所见的有一些不同。要了解详细的内容,见“三维坐标系统”部分。
下面的变换将一个点(x, y, z)沿x-轴进行旋转,得到了一个新的点(x', y', z'):
下面的变化沿y-轴进行旋转:
下面的变换沿z-轴进行旋转:
这里要注意一点,希腊字母θ代表旋转的角度,用弧度来表示。从旋转轴向原点看,这个角度按顺时针方向来度量。
你可以使用D3dutil.cpp文件中的RotateX, RotateY, 和RotateZ辅助函数来创建旋转矩阵。下面是RotateX函数的代码:
| D3DMATRIX RotateX(const float rads) { float cosine, sine; cosine = cos(rads); sine = sin(rads); D3DMATRIX ret = IdentityMatrix(); ret(1,1) = cosine; ret(2,2) = cosine; ret(1,2) = -sine; ret(2,1) = sine; return ret; } // end of RotateX() |
2.4 缩放
下面的变换在x-, y-, 和z-方向选择任意的值对点(x, y, z)进行缩放,得到一个新的点(x', y', z'):
2.5 矩阵级联
我们使用矩阵的一个最大好处就是可以通过矩阵相乘来将几个矩阵变换的效果合并起来。这就是说,当我们对一个模型进行旋转和平移时,不再需要用到两个矩阵。我们可以通过将旋转矩阵与平移矩阵相乘来得到一个合并的矩阵。这一过程就被称为矩阵级联,可以用下面的公式来表示:
![]()
共识中,C指组合之后产生的新矩阵,M1到Mn表示要组合在一起的每一个矩阵。一般情况下,我们指将两或三个矩阵组合起来,但实际上是没有限制的。
D3dmath.cpp源文件中有一个D3DMath_MatrixMultiply辅助函数来进行矩阵级联运算。
在进行矩阵级联时,我们应该注意级联时的顺序。上面公式中反映的是一种从右到左的矩阵级联规则。也就是说,我们用来创建一个合并的矩阵的每个矩阵的实际效果是从右到左依次出现的。下面我们举一个例子来说明这一情况。在这个例子中,我们要通过世界变换矩阵来创建一个“飞碟”。我们想要这个UFO沿中心(模型空间的y-轴)来旋转,同时要在场景中平移。为了达到这样的效果,你可以首先创建一个平移矩阵,然后用它和旋转矩阵相乘,如下所示:
W=Tw·Ry
公式中,Tw表示平移矩阵,Ry表示旋转矩阵。
两个矩阵相乘的顺序是很重要的,与标量的相乘不同,矩阵相乘的顺序是不能交换的。如果我们将两个矩阵的顺序交换的话,得到的结果就会是,先对飞碟进行平移,然后将它绕世界原点进行旋转。
无论我们创建什么类型的矩阵,都要按照从右到左的顺序,这样才能达到我们预期的结果。