人工智能中对机器学非常简要的介绍

Very Brief Introduction to Machine Learning for AI¶

The topics summarized here are covered in these slides.

本主题总结的内容包含在这些幻灯片中。

Intelligence（智能）

The notion of intelligence can be defined in many ways. Here we define it as the ability to take the right decisions, according to some criterion (e.g. survival and reproduction, for most animals). To take better decisions requires knowledge, in a form that is operational, i.e., can be used to interpret sensory data and use that information to take decisions.

智能的概念可以用很多种方式来定义。本文中，我们把他定义为参照某些标准（例如， 大多数动物的生存和繁殖）做出正确决策的能力。要做出更好的决策，需要可操作形式的知识的支撑，例如，可以用于转化感觉数据，并使用转化的信息来决定。

Artificial Intelligence（人工智能）

Computers already possess some intelligence thanks to all the programs that humans have crafted and which allow them to “do things” that we consider useful (and that is basically what we mean for a computer to take the right decisions). But there are many tasks which animals and humans are able to do rather easily but remain out of reach of computers, at the beginning of the 21st century. Many of these tasks fall under the label of Artificial Intelligence, and include many perception and control tasks. Why is it that we have failed to write programs for these tasks? I believe that it is mostly because we do not know explicitly (formally) how to do these tasks, even though our brain (coupled with a body) can do them. Doing those tasks involve knowledge that is currently implicit, but we have information about those tasks through data and examples (e.g. observations of what a human would do given a particular request or input). How do we get machines to acquire that kind of intelligence? Using data and examples to build operational knowledge is what learning is about.

基于人类编写的让计算机“做一些事情”的代码，计算机已经可以做一些我们认为有意义的只能的事情（那基本上是我们让一台电脑做正确决策的意思）。但是，在第二十一世纪初，仍然有很多事情人类和动物可以很容易地完成，但是计算机却不能完成。Many of these tasks fall under the label of Artificial Intelligence，包括许多感知和控制任务。为什么我们写不成代码来完成这些任务呢？我觉得主要是因为我们还没有清楚（正式）的知道如何做这些事情，虽然我们有一个大脑（加上一个身躯）可以完成他们。完成这些事情需要一些目前隐含存在的知识的支撑，but we have information about those tasks through data and examples（如，观察在给出特定的需求或者输入的时候，一个人会做什么）。我们怎样让机器来获得这种智能呢？用数据和实例来构建可操作的知识就学习要做的事情。

Machine Learning（机器学习）

Machine learning has a long history and numerous textbooks have been written that do a good job of covering its main principles. Among the recent ones I suggest:

机器学习的历史非常长远，已经有非常多的不错的书包含了机器学习的主要原理。建议读以下书籍：

• Chris Bishop, “Pattern Recognition and Machine Learning”, 2007
• 模式识别和机器学习

• Simon Haykin, “Neural Networks: a Comprehensive Foundation”, 2009 (3rd edition)
•  神经网络： 综合基础 
  

• Richard O. Duda, Peter E. Hart and David G. Stork, “Pattern Classification”, 2001 (2nd edition)
• 模式分类

Here we focus on a few concepts that are most relevant to this course.

下面就本文相关的一些主要概念做解释。

Formalization of Learning（形式化学习 ？）

First, let us formalize the most common mathematical framework for learning. We are given training examples

with the  being examples sampled from an unknown process . We are also given a loss functional  which takes as argument a decision function  and an example , and returns a real-valued scalar. We want to minimize the expected value of  under the unknown generating process .

首先，让我们形式化机器学习中最常见的计算框架。我们给出训练实例

其中 为未知过程 的一个样本。我们给出作为决策函数 的参数的损失函数 ， 一个样本 , 和一个实值的标量返回值。 我们希望最小化在未知产生函数 下的期望值

Supervised Learning（监督式学习）

In supervised learning, each examples is an (input,target) pair:  and  takes an  as argument. The most common examples are

在监督是学习中，每一个样本个是一个（输入，目标）对偶：， 为 的参数。最常见的例子如下

• regression: 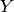 is a real-valued scalar or vector, the output of  is in the same set of values as 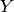, and we often take as loss functional the squared error
• 回归： 是一个实值的标量或者向量， the output of 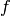 is in the same set of values as , 通常取平方误差为损失函数。
  

• classification（分类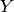）:  is a finite integer (e.g. a symbol) corresponding to a class index, and we often take as loss function the negative conditional log-likelihood, with the interpretation that  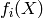estimates :

  

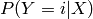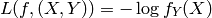
  where we have the constraints（这里的约束为）

  

Unsupervised Learning（非监督式学习）

In unsupervised learning we are learning a function  which helps to characterize the unknown distribution . Sometimes  is directly an estimator of  itself (this is called density estimation). In many other cases  is an attempt to characterize where the density concentrates. Clustering algorithms divide up the input space in regions (often centered around a prototype example or centroid ). Some clustering algorithms create a hard partition (e.g. the k-means algorithm) while others construct a soft partition (e.g. a Gaussian mixture model) which assign to each  a probability of belonging to each cluster. Another kind of unsupervised learning algorithms are those that construct a new representation for . Many deep learning algorithms fall in this category, and so does Principal Components Analysis.

在无监督学习中，我们要学习一个函数  来描述未知分布 。通常 是对 本身的一个估计（密度估计）。在许多其他情况下，  尝试描述哪里是密度中心。聚类算法按照区域（通常围绕一个原始的样本的或质心）划分输入空间。一些聚类算法创建一个硬划分（如，k-均值算法），而其他构建一个软划分（如高斯混合模型），并分配给每个 一个概率表示属于每个聚簇的可能性。另一类无监督的学习算法是一类构造  的新表示的算法，许多深度学习算法属于这一类，另外主成分分析（PCA）也是。

Local Generalization（局部泛化）

The vast majority of learning algorithms exploit a single principle for achieving generalization: local generalization. It assumes that if input example  is close to input example , then the corresponding outputs  and  should also be close. This is basically the principle used to perform local interpolation. This principle is very powerful, but it has limitations: what if we have to extrapolate? or equivalently, what if the target unknown function has many more variations than the number of training examples? in that case there is no way that local generalization will work, because we need at least as many examples as there are ups and downs of the target function, in order to cover those variations and be able to generalize by this principle. This issue is deeply connected to the so-called curse of dimensionality for the following reason. When the input space is high-dimensional, it is easy for it to have a number of variations of interest that is exponential in the number of input dimensions. For example, imagine that we want to distinguish between 10 different values of each input variable (each element of the input vector), and that we care about about all the  configurations of these  variables. Using only local generalization, we need to see at least one example of each of these  configurations in order to be able to generalize to all of them.

Distributed versus Local Representation and Non-Local Generalization（分布式 VS 局部表示和非局部泛化）

A simple-minded binary local representation of integer  is a sequence of  bits such that , and all bits are 0 except the -th one. A simple-minded binary distributed representation of integer  is a sequence of  bits with the usual binary encoding for . In this example we see that distributed representations can be exponentially more efficient than local ones. In general, for learning algorithms, distributed representations have the potential to capture exponentially more variations than local ones for the same number of free parameters. They hence offer the potential for better generalization because learning theory shows that the number of examples needed (to achieve a desired degree of generalization performance) to tune  effective degrees of freedom is .

Another illustration of the difference between distributed and local representation (and corresponding local and non-local generalization) is with (traditional) clustering versus Principal Component Analysis (PCA) or Restricted Boltzmann Machines (RBMs). The former is local while the latter is distributed. With k-means clustering we maintain a vector of parameters for each prototype, i.e., one for each of the regions distinguishable by the learner. With PCA we represent the distribution by keeping track of its major directions of variations. Now imagine a simplified interpretation of PCA in which we care mostly, for each direction of variation, whether the projection of the data in that direction is above or below a threshold. With  directions, we can thus distinguish between  regions. RBMs are similar in that they define  hyper-planes and associate a bit to an indicator of being on one side or the other of each hyper-plane. An RBM therefore associates one input region to each configuration of the representation bits (these bits are called the hidden units, in neural network parlance). The number of parameters of the RBM is roughly equal to the number these bits times the input dimension. Again, we see that the number of regions representable by an RBM or a PCA (distributed representation) can grow exponentially in the number of parameters, whereas the number of regions representable by traditional clustering (e.g. k-means or Gaussian mixture, local representation) grows only linearly with the number of parameters. Another way to look at this is to realize that an RBM can generalize to a new region corresponding to a configuration of its hidden unit bits for which no example was seen, something not possible for clustering algorithms (except in the trivial sense of locally generalizing to that new regions what has been learned for the nearby regions for which examples have been seen).