Word2vec基础介绍（四）：CBOW和skip-gram模型

CBOW和skip-gram应该可以说算是word2vec的核心概念之一了。这一节我们就来仔细的阐述这两个模型。其实这两个模型有很多的相通之处，所以这里就以阐述CBOW模型为主，然后再阐述skip-gram与CBOW的不同之处。

1.CBOW模型

之前已经解释过，无论是CBOW模型还是skip-gram模型，都是以Huffman树作为基础的。而Huffman树的构建在前一节已经讲过咯，这里就不再重复。值得注意的是，Huffman树中非叶节点存储的中间向量的初始化值是零向量，而叶节点对应的单词的词向量是随机初始化的。

1.1 训练的流程

那么现在假设我们已经有了一个已经构造好的Huffman树，以及初始化完毕的各个向量，可以开始输入文本来进行训练了。

训练的过程如下图所示，主要有输入层(input)，映射层(projection)和输出层(output)三个阶段。

输入层即为某个单词A周围的n-1个单词的词向量。如果n取5，则词A(可记为w(t))前两个和后两个的单词为w(t-2),w(t-1),w(t+1),w(t+2)。相对应的，那4个单词的词向量记为v(w(t-2)),v(w(t-1)),v(w(t+1)),v(w(t+2))。从输入层到映射层比较简单，将那n-1个词向量相加即可。而从映射层到到输出层则比较繁琐，下面单独讲

1.2 从映射层到输出层

要完成这一步骤，需要借助之前构造的Huffman树。从根节点开始，映射层的值需要沿着Huffman树不断的进行logistic分类，并且不断的修正各中间向量和词向量。

举个例子, 比如说有下图所示的Huffman树

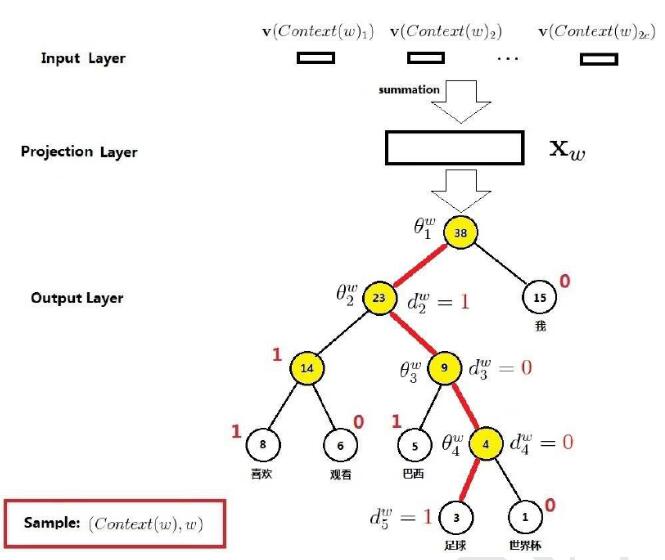
此时中间的单词为w(t)，而映射层输入为
pro(t)=v(w(t-2))+v(w(t-1))+v(w(t+1))+v(w(t+2))

假设此时的单词为“足球”，即w(t)=“足球”，则其Huffman码可知为d(t)=”1001”(具体可见上一节),那么根据Huffman码可知，从根节点到叶节点的路径为“左右右左”，即从根节点开始，先往左拐，再往右拐2次，最后再左拐。

既然知道了路径，那么就按照路径从上往下依次修正路径上各节点的中间向量。在第一个节点，根据节点的中间向量Θ(t,1)和pro(t)进行Logistic分类。如果分类结果显示为0，则表示分类错误(应该向左拐，即分类到1)，则要对Θ(t,1)进行修正，并记录误差量。

接下来，处理完第一个节点之后，开始处理第二个节点。方法类似，修正Θ(t,2)，并累加误差量。接下来的节点都以此类推。

在处理完所有节点，达到叶节点之后，根据之前累计的误差来修正词向量v(w(t))。

这样，一个词w(t)的处理流程就结束了。如果一个文本中有N个词，则需要将上述过程在重复N遍，从w(0)~w(N-1)。

1.3 CBOW模型的伪代码描述

将模型形象化的描述过以后，还需要以更精确的方式将模型的流程确定下来。
首先，我们需要先引入一些符号以便于更清晰的表达。

那么根据word2vec中的数学，流程可以表述为

其中σ表示sigmoid函数，η表示学习率。学习率越大，则判断错误的惩罚也越大，对中间向量的修正跨度也越大。

1.4 CBOW模型的代码描述

为了提高复用性，代码主要由两部分组成，分别是__Deal_Gram_CBOW和__GoAlong_Huffman。后者负责最核心部分，也就是与huffman相关的部分，前者负责剩下的功能，包括修正词向量等

def __Deal_Gram_CBOW(self,word,gram_word_list):

        if not self.word_dict.__contains__(word):
            return

        word_huffman = self.word_dict[word]['Huffman']
        gram_vector_sum = np.zeros([1,self.vec_len])
        for i in range(gram_word_list.__len__())[::-1]:
            item = gram_word_list[i]
            if self.word_dict.__contains__(item):
                gram_vector_sum += self.word_dict[item]['vector'] #将周围单词的词向量相加
            else:
                gram_word_list.pop(i)

        if gram_word_list.__len__()==0:
            return

        e = self.__GoAlong_Huffman(word_huffman,gram_vector_sum,self.huffman.root) #与Huffman相关方法

        for item in gram_word_list:
            self.word_dict[item]['vector'] += e
            self.word_dict[item]['vector'] = preprocessing.normalize(self.word_dict[item]['vector']) #修正词向量

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23

def __GoAlong_Huffman(self,word_huffman,input_vector,root):

        node = root     #从root开始 自顶向下
        e = np.zeros([1,self.vec_len])  #将误差初始化为零向量
        for level in range(word_huffman.__len__()):  # 一层层处理
            huffman_charat = word_huffman[level] # 根据Huffman码获知当前节点应该将输入分到哪一边
            q = self.__Sigmoid(input_vector.dot(node.value.T))
            grad = self.learn_rate * (1-int(huffman_charat)-q) # 计算当前节点的误差
            e += grad * node.value # 累加误差
            node.value += grad * input_vector #修正当前节点的中间向量
            node.value = preprocessing.normalize(node.value) # 归一化
            if huffman_charat=='0': #将当前节点切换到路径上的下一节点
                node = node.right
            else:
                node = node.left
        return e

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16

2. skip-gram模型

skip-gram与CBOW相比，只有细微的不同。skip-gram的输入是当前词的词向量，而输出是周围词的词向量。也就是说，通过当前词来预测周围的词。如下图所示

由于输出有n-1个词，所以要对于一个词来讲，上述沿着huffman树从顶到底的过程要循环n-1遍。。。其伪码描述如下

其代码描述如下，与huffman有关的代码上面已经贴过了，就不再重复

def __Deal_Gram_SkipGram(self,word,gram_word_list):

        if not self.word_dict.__contains__(word):
            return

        word_vector = self.word_dict[word]['vector']
        for i in range(gram_word_list.__len__())[::-1]:
            if not self.word_dict.__contains__(gram_word_list[i]):
                gram_word_list.pop(i)

        if gram_word_list.__len__()==0:
            return

        for u in gram_word_list:
            u_huffman = self.word_dict[u]['Huffman']
            e = self.__GoAlong_Huffman(u_huffman,word_vector,self.huffman.root)
            self.word_dict[word]['vector'] += e
            self.word_dict[word]['vector'] = preprocessing.normalize(self.word_dict[word]['vector'])

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19