Python3学习(10)--列表生成器（List generator）

上一篇我们讲到了，列表生成式，花里胡哨的，但是很实用，我们在回顾一下一个简单生成式的构造：

这里我们构造一个x*x的list，元素10个：

 

如下：

 

 

我们可以清楚的看到我们想要的结果，这种L就是利用列表生成式产生的list对象

 

       本篇讲到的，生成器(generator)区别于生成式(generation)但二者之间又是有亲密联系的，从字面上理解，生成器就是存放生成式产生结果的容器，说具体点就是，存放list的容器，有些人肯定说了，list本来就是一个集合，还需要再用其他容器放吗？我们打个比方，我们之前学过迭代器(iterator)，我们知道只要能for循环遍历的对象就是可迭代的对象，而可迭代的对象就能通过函数iter(可迭代对象)获得对应的迭代器对象，通过next方法，我们就可以一一获得可迭代对象的元素或者key，当然，我们这里讲的生成器，其实它也是迭代对象，因为它也是可以next的，只不过它是针对生成式产生的list对象的迭代器，我们就称作列表生成器。

 

上面说的有点抽象了，都是个人理解的，不过本篇结束后，相信我们应该对什么是生成器有个清晰的理解了。

 

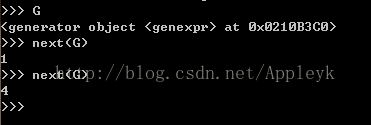
针对上面的例子，我们改下，我们用"（.....）"代替"[....]",将生成式括起来：

 

 

 

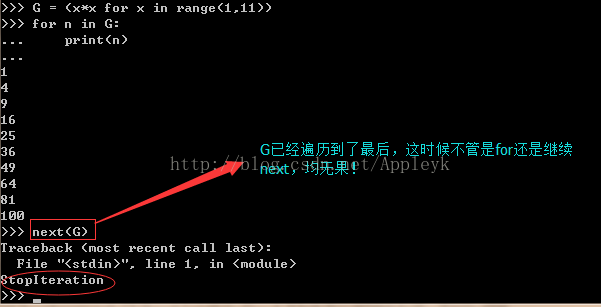
我们发现，这个对象还在内存中对应一块地址，上面说过，这个对象也是一种迭代对象，因此，我们尝试几个next，试图读出几个元素：

 

 

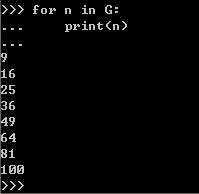
如果一直next下去，肯定还会输出元素的，直到StopIteration抛出；从这一点可以看出，我们的generator是一个迭代对象，也是可以迭代的，因此，我们用for循环遍历G中的元素（这种不需要考虑StopIteration）：

 

 

 

以上我们对什么是生成器有了个初步的认识，下面我们再来学习一个可以产生generator对象的函数--- yield()

讲之前，我们执行一个简单的输出函数：

 

A：

 

#!/usr/bin/env python3
# encoding:utf-8
def Test01():
	print("执行----------A")
	print("执行----------B")
	print("执行----------C")      
Test01()

 

执行结果：

 

 

 

我们改下

 

B:

 

#!/usr/bin/env python3
# encoding:utf-8

def Test01():
	print("执行----------A")
	return "A"
	print("执行----------B")
	return "B"
	print("执行----------C")
	return ("C")
print(Test01())

执行结果：

 

 

这个我们很好理解，函数return后，下面的就不会执行了，函数的任务也就完成了，所以，这种情况，只会输出A。

 

 

我们再改下，这次我们用到函数yield()，看下它的魔法效果：

 

C：

 

#!/usr/bin/env python3
# encoding:utf-8

def Test01():
	print("执行----------A")
	yield('A')
	print("执行----------B")
	yield('B')
	print("执行----------C")
	yield('C')
Test01() #这里我们试图直接调用方法，看下一开始是否调用print打印信息
print(Test01()) #这里我们只是猜测一下Test01函数会返回一些东西，当然我们现在还不知道？

 

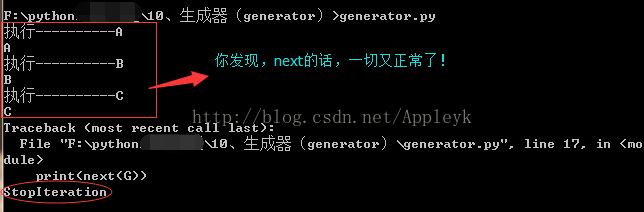
执行结果：

 

 

what？这输出的什么鬼，为什么直接调用函数，没有一条输出，反而输出了个这，别急，我们看下，噢，这原来是个generator对象啊，但是，这个对象是从哪冒出来的？因此，yield这个家伙还是很可疑的，我们发现，连我们的print("执行----------A")的这个最应该输出的都没有输出，是什么情况呢？

 

这里就不饶关子了，直接来解密下这个高深莫测的现象：

 

函数一般都是顺序执行的，当遇到return或者执行到最后一条语句时，就会结束，而函数内部的一切操作都会"暴露"出来，而具有generator性质的函数则不是按常理出牌，而是，当遇到yield的时候，函数其实已经被控制了，这时候调用函数，你会发现什么也不输出，但是你把这个函数打印出来，你会发现返回的是一个generator对象，我们就想到，既然是generator对象，我们用next测试一下，不，是测试几下，我们先看修改后的代码：

 

D：

 

def Test01():
	print("执行----------A")
	yield('A')
	print("执行----------B")
	yield('B')
	print("执行----------C")
	yield('C')
#Test01() 既然直接调用没有任何卵用，这行注释
#既然我们知道这个函数是generator性质的,我们用一个变量存下这个对象
G = Test01()
print(next(G))
print(next(G))
print(next(G))
print(next(G))
'''
print("上面为next，下面为for")

for n in G:
    print(n) #这里什么也不出，因为G已经被榨干！

#这里要说一下，我们也可以用for循环进行遍历
#但是，我们如果对G进行一次遍历后，再进行遍历的时候，就不行了
#因为，G本身就是一个迭代器，无论是for遍历还是一直next
#都是在消耗next的，所以，遍历到最后，next已用尽
#也就是数据指针已经指向了不可预测的地址，这时候，会抛出StopIteration
'''

 

我们看下结果：

 

 

我们可以这样理解，next相当于一个开关，一旦触碰到了这个开关，函数未执行的部分就会继续执行，直到这个开关失灵（遇到了StopIteration）,当然我们实际上，很少这样玩，函数会被玩坏的，这样的输出看上去真的很糟糕，但是我们却可以控制函数的输出，是不是很随心所欲。

 

现在休息一会，插播一条需要注意的地方：

生成器，每次遍历都会耗费一次next，当next到尽头，生成器从此不再被世人所记住！

 

 

 

我们再看下，迭代器：

 

 

 

上面，我们发现，迭代器是有"生命周期的",而可迭代的对象比如list却可以随便for循环遍历N次都没事，因此，我们再次修改以上代码：

 

#!/usr/bin/env python3
# encoding:utf-8

def Test01():
	print("执行----------A")
	yield('A')
	print("执行----------B")
	yield('B')
	print("执行----------C")
	yield('C')
#Test01() 既然直接调用没有任何卵用，这行注释
#既然我们知道这个函数是generator性质的,我们用一个变量存下这个对象
G = Test01()
L=list(G)#这里，会把Test01函数里没有输出的三个print打印出来，而将'A','B','C'保存到列表中
for n in L:
	print(n)

for n in L:
	print(n)#你会发现，这里，循环将不再受next的影响，因为此时generator已经转换成了一个list对象

 

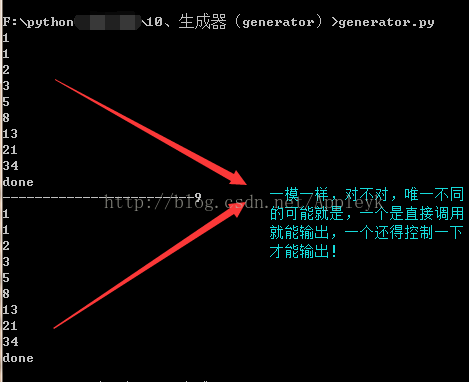
看下输出结果：

 

 

通过上面的学习，我们已经掌握了yield的用法，准确说是generator的用法，下面，我们趁热打铁，再来一个例子：

我们直接上demo，注释已经很详细了，不再多做解释：

 

#!/usr/bin/env python3
# encoding:utf-8

'''
著名的斐波拉契数列（Fibonacci）:
除第一个和第二个数外，任意一个数都可由前两个数相加得到
1, 1, 2, 3, 5, 8, 13, 21, 34, ...
'''
def flib_1(max):
	
	#n:循环次数，有几个数循环几次，初始化1
	#a:代表前一个的数，最开始1前面应该没有数，我们初始化0
	#b:代表后一个的数，最开始的两个数必然相等，后面的数就是b(new)=a+b(old)，初始化1
    #因此这里有个小细节，也就是我们在算新值的时候，也要保存下旧值
	n,a,b = 1,0,1 	
	while n<=max: #每当数字往后推进的时候，我们保存下旧值，算下新值
		print(b) #这里，我们打印出当前位置上的number	
		temp = b #这里，我们用一个临时变量temp保存下旧的b值
		b=a+temp #这里，我们算下新的值
		a=temp   #这里，我们更新下新值的前一个数，a和b必须保持同步
		n = n+1  #这里，我们推进下一个数
	return 'done'#这里，我们结束斐波拉契数列的计算

print(flib_1(9))
print("------------------------9")
#我们将上面的普通函数改为generator性质的函数

def flib_2(max):
	n,a,b = 1,0,1 	
	while n<=max:
		yield(b) 
		a,b=b,a+b; #我们也可以这样写，简单粗暴（我会时不时的重复这四个字，哈哈） 
		n = n+1  
	return 'done'#这里，我们结束斐波拉契数列的计算

G = flib_2(9)
while True:
	try:
		n = next(G)
		print(n)
	except StopIteration as e: #为了取出函数最后的返回值，我们利用异常捕获获得
		print(e.value)         #返回值包含在异常消息StopIteration的value中
		break

 

我们看下结果：

 

 

 

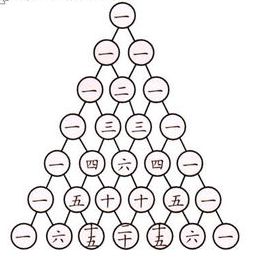
以上如果我们还是不过瘾的话，我们在尝试在写一个例子，这个例子就是有名的杨辉三角：

 

 

如图所示，我们可以看出来，顶端往下，两边都是1，中间的数据部分，是前一个数列的相邻两个数的和，当然，得保证两边是1，我们分解下上图：

 

 

 

好了，根据以上的图解，我们知道，在开始前，我们肯定要初始化一个L，像这样：

 

L = [1]

 

每一次输出的时候我们用yield（L）控制一下，使他返回一个generator对象，随后，我们再给之前的L添加一个元素，这个元素就是0，实际是追加到list末尾的，我们用append()-->L.append(0)

 

当然我们要用到循环，而循环不能无限循环下去，我们需要给个条件，比如，当我们当前的L的长度超过某个值时，我们把这个值用参数max代替，表示，当前杨辉三角所能输出的最大列，这个时候，break，我们这样做-->

 

if len(L)>=max:
            break

 

好了，如果上面不满足的话，我们就利用列表生成式来生成我们想要的list了，很简单，如下：

 

L=[L[n-1]+L[n] for n in range(len(L))]

 

注意，range（len（L））这个，只是用来取索引的，所以是从0开始的，有人会问，当n=0的时候，n-1 = -1 啊，会不会越界提示啊？不会的，因为我们学过list的访问方式，既可以正着来，也可以反着来，-1正好是倒数第一个元素，而倒数第一个元素在这里正好体现的是0这个元素，因此，左边的第一个元素始终都是1

 

好了，上面基本上讲解完了，下面我们看下demo实现部分：

 

#!/usr/bin/env python3
# encoding:utf-8

def triangles(max):
	L=[1]
	while True:
		yield(L)    #generator生成器会存下这个L
		if len(L)>=max:
			break
		L.append(0) #注意：每次产生一列的时候，紧接着就是在这一列的后面追加一个0元素以作为新的列的基础
		L=[L[n-1]+L[n] for n in range(len(L))]
       
'''
1--------------------------------------直接输出------------------------------------------->[1]
2-------->[1,0]------------------>len(L)=2,L=[L[-1]+L[0],L[0]+L[1]]----------------------->[1,1]
3-------->[1,1,0]---------------->len(L)=3,L=[L[-1]+L[0],L[0]+L[1],L[1]+L[2]]------------->[1,2,1]
4-------->[1,2,1,0]-------------->len(L)=4,L=[L[-1]+L[0],L[0]+L[1],L[1]+L[2],L[2]+L[3]]--->[1,3,3,1]
5---------------------------
6---------------------------

'''

for n in triangles(7):
	print(n) #最后输出结果，注意这个n其实是一个个list对象

 

我们来看下我们的杨辉三角dos版长什么样（迫不及待啊）：

 

 

 

 

我们再来看下代码，不加输出总过8行代码，我们就实现了这么复杂的算法（这种复杂只是相对的，你可以用java，C#等语言写写这个杨辉三角，你会发现，10行代码你根本搞不定的），所以，我们在刚接触生成式的时候，可能并不知道它究竟能干出什么伟大的事情来，现在知道了吧，还有生成器，二者结合的也很完美；

 

 

 

本篇结束：

从第一篇写到现在，我慢慢发现，自己对于python的理解已经有所改变，我以为它是在"胡来"，没想到却来的那么理直气壮，让人不得不服；这只是皮毛，python这趟水，我已踏入，是不是不归路，我不知道，我只知道， 我已经爱上它了。