有趣的思路题集锦from bzoj/codefoces(乱搞)
1、题目:Codefoces #371C
Hamburgers
题解:
没有想到二分的我代码写的冗长而且是错的。。。
即使只有三个也很难枚举清楚呢
二分可以很好解决啦
代码:
#include if (st[i]=='B') b++;
else if (st[i]=='S') s++;
else c++;
scanf("%I64d%I64d%I64d%I64d%I64d%I64d%I64d",&nb,&ns,&nc,&pb,&ps,&pc,&rr);
while (l<=r)
{
LL mid=(l+r)>>1;
LL x=max(0ll,b*mid-nb),y=max(0ll,s*mid-ns),z=max(0ll,c*mid-nc);
LL f=x*pb+y*ps+z*pc;
if (f<=rr) l=mid+1;else r=mid-1;
}
printf("%I64d",l-1);
} =========
2、题目:BZOJ 2456
Mode
题解:
把数字们对对碰,因为是众数的话肯定能碰掉其他所有的数字啊
代码:
#include =========
3、题目:BZOJ 3713
Iloczyn
题解:
看起来好复杂,但是我仔细一看,发现n最大竟然是1e9?
那我光把小于1e9的fib的记录下来——哇一共才44个,那就 O(Tn2) 枚举吧
代码:
#include =========
4、题目:BZOJ 3043
IncDec Sequence
题意:
给定一个长度为n的数列{a1,a2…an},每次可以选择一个区间[l,r],使这个区间内的数都加一或者都减一。
问至少需要多少次操作才能使数列中的所有数都一样,并求出在保证最少次数的前提下,最终得到的数列有多少种。
对于100%的数据,n=100000,0<=ai<2147483648
题解:
对于带有“将一段区间内的每个数全部加上某个值”这种操作的题目,通常考虑差分原数列以简化情况,将对一段区间的操作转化为对某两个特定数的操作。
我们定义 d1=a1,di=ai−ai−1(2≤i≤n),dn+1=0 (事实上,稍后我们会看到d_1和d_{n+1}的值并不重要),可以发现,原题中的“将[l,r]内的数都加一或都减一”将对应“将 dl+1,将dr+1−1 ”(或反之)的操作。
显然,题目中要求的a数列中的所有数全部相等的条件等同于使 di=0(2≤i≤n) ,最后数列中的数即为 d1 ,而题目中的操作允许我们把d数列中的某个数+1,某个数-1。
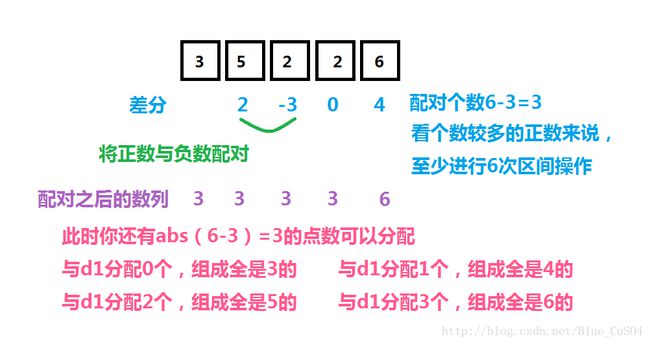
要将d数列中第二项至第n项全部变为0并使操作次数最少,首先我们将每个负数和每个正数配对执行操作,设d数列中第2至第n项所有正数分别求和得到的值为p,负数分别求和得到的值的绝对值为q,这一步的操作次数即为min{p,q}。
此时还剩余和的绝对值为abs(p-q)的数没有变为0,每次操作我们可以将其与 d1 或 dn+1 配对进行操作,操作次数为abs(p-q),容易看出,最终 d1 的可能取值有abs(p-q)+1种。因此,第一问的答案即为max{p,q},第二问的答案即为abs(p-q)+1。
清晰的图示!
代码:
#include
#define M 100100
using namespace std;
int n;long long a[M],pos,neg;
int main()
{
int i;scanf("%d",&n);
for(i=1;i<=n;i++) scanf("%lld",&a[i]);
for(i=n;i>1;i--)
if(a[i]-a[i-1]>0) pos+=a[i]-a[i-1];
else neg+=a[i-1]-a[i];
printf("%lld\n%lld",max(pos,neg),abs(pos-neg)+1);
return 0;
} =========
5、题目:BZOJ 3725
PA2014 Final Matryca刷墙
题解:
我们可以从题目的描述来推起:“你需要用这把刷子在墙上每一个可能的位置(只要刷子不超出墙,且对准格子;共有n-k+1个位置)都刷一遍”
也就是说假如刷子长为k的话,1~n-k+1的颜色必须一样,类推一下就是i~n-k+i的颜色都要是一样的。也就是说在这个区间内,要不是*号,要不就是颜色全都一样
那我们只要求出符合这要求的所有区间的min值就是n-k+1的值啦
代码:
#include if (st[i]!='*')
{
if (!last) last=st[i],now=i;
else if (last!=st[i])
{
minn=min(minn,i-now);
last=st[i]; now=i;
}else now=i;
}
printf("%d",l-minn+1);
} =========
6、题目:Codefoces #354B
Pyramid of Glasses
题解:
看上去就很害怕
这个t的时间就是告诉你有多少水
但是仔细想想就会发现好像和杨辉三角有什么关系,因为一个瓶子里的水溢出来的话只会溢到a[i+1][j]和a[i+1][j+1]的瓶子里
每次还是只溢出来上次的二分之一,当然要先给上边桶留上1啊
代码:
#include