天平难题 UVa 1354

给出房间的宽度r和s个挂坠的重量wi，设计一个尽量宽（但宽度不能超过房间宽度r）的天平，挂着所有挂坠。 

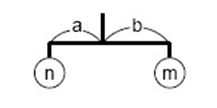
天平由一些长度为1的木棍组成。木棍的每一端要么挂一个挂坠，要么挂另外一个木棍。如下图所示，设n和m分别是两端的总重量，要让天平平衡，必须满足n*a=m*b。

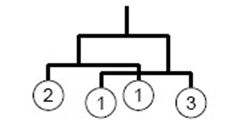
挂坠的宽度忽略不计，且不同的子天平可以相互重叠，下图所示如。

输入第一行为数据组数。每组数据前两行为房间宽度r和挂坠数目s （0 < r < 10,1<=s<=6）。以下s行为一个挂坠的重量wi（1<=wi<=1000）。输入保证不存在天平的宽度恰好在r-10^(-5)和r+10^(-5)（这样可以保证不会出现精度问题）。对于每组数据，输出最优天平的宽度。如果无解，输出-1。你的输出和标准答案的绝对误差不应超过10^(-8)。

题解：

一个天平可看做一棵二叉树，对于一个确定的二叉树，可以算出每一个挂坠的位置，那么这个天平的宽度也可以计算出来，那么问题就转化成了枚举所有的二叉树。

在这里给出三种方法。

方法一：

自底上向上构造，每次任选择2个挂坠合并为一个。

#include
#include
#include
#include
#define f(i,l,r) for(i=(l);i<=(r);i++)
using namespace std;
const int MAXN=8;
double W,w[MAXN],ans,l[MAXN],r[MAXN];
int n,vis[MAXN];
inline void dfs(int cur)
{
	int i,j;
	if(cur==n){
		f(i,1,n){
			if(vis[i]) continue;
			if(l[i]+r[i]>W) continue;
			ans=max(ans,l[i]+r[i]);
		}
		return;
	}
	f(i,1,n){
		if(vis[i]) continue;
		f(j,1,n){
			if(i==j||vis[j]) continue;
			vis[i]=1;
			double a=w[j]/(w[i]+w[j]),b=1-a;
			w[j]+=w[i];
			double tmpl=l[j],tmpr=r[j];
			l[j]=max(l[i]+a,-b+l[j]);
			r[j]=max(r[j]+b,-a+r[i]);
			dfs(cur+1); 
			vis[i]=0;
			w[j]-=w[i];
			l[j]=tmpl;
			r[j]=tmpr;
		}
	}
}
int main()
{
	ios::sync_with_stdio(false);
	int i,j,T;
	cin>>T;
	while(T--){
		memset(vis,0,sizeof(vis));
		memset(l,0,sizeof(l));
		memset(r,0,sizeof(r));
		ans=-1;
		cin>>W>>n;
		f(i,1,n){
			cin>>w[i];
		}
		dfs(1);
		cout<

方法二：自顶向下回溯构造，用一个一维数组保存二叉树，i的父亲就是i+i。

#include
#include
#include
#include
#define f(i,l,r) for(i=(l);i<=(r);i++)
#define ff(i,r,l) for(i=(r);i>=(l);i--)
using namespace std;
const int MAXN=8;
double w[MAXN],W,l[1<W) return; 
		}
	}
	ans=max(ans,l[1]+r[1]);
} 
inline void dfs(int cur,int pos,int res)
{
	int i;
	if(res==0){
		judge(cur-1);
		return;
	}
	if(~tree[cur>>1]){
		dfs(cur+1,pos,res);
		return;
	}
	if(pospos) return;
	f(i,1,n){
		if(vis[i]) continue;
		vis[i]=1;
		tree[cur]=i;
		dfs(cur+1,pos-1,res-1); 
		vis[i]=0;
	}
}
int main()
{
	ios::sync_with_stdio(false);
	int i,j,T;
	cin>>T;
	while(T--){
		memset(vis,0,sizeof(vis));
		memset(tree,0,sizeof(tree));
		ans=-1;
		cin>>W>>n;
		f(i,1,n){
			cin>>w[i];
		}
		if(n==1){                       //necessary special judge
			cout<<0<

方法三：自顶向下枚举子集构造，每次枚举左子树用到哪些子集，那么右子树就是剩下的子集，递归构造即可，另外根据对称性，一个子集若已经构造过，那么剪枝。

#include
#include
#include
#include
#include
#define f(i,l,r) for(i=(l);i<=(r);i++)
using namespace std;
const int MAXN=10;
struct Tree{
	double l,r;
};
vector tree[MAXN<<3];
double w[MAXN],W,sum[MAXN<<3],ans;
int n,vis[MAXN<<3];
inline void dfs(int S)
{
	int i,j,l,r,flag=1;
	if(vis[S]) return;
	vis[S]=1;
	for(l=(S-1)&S;l;l=(l-1)&S){
		flag=0;
		r=S^l;
		double d1=sum[r]/sum[S];
		double d2=sum[l]/sum[S];
		dfs(l);
		dfs(r);
		for(i=0;i>T;
	while(T--){
		cin>>W>>n;
		memset(sum,0,sizeof(sum));
		memset(vis,0,sizeof(vis));
		f(i,1,n){
			cin>>w[i];
		}
		f(i,1,(1<