gitchat训练营15天共度深度学习入门课程笔记(四)
第3章 神经网络
- 3.4 3 层神经网络的实现
- 3.4.1 符号确认
- 3.4.2 各层间信号传递的实现
- 3.4.3 代码实现小结
- 3.5 输出层的设计
- 3.5.1 恒等函数和 softmax 函数
- 3.5.2 实现 softmax 函数时的注意事项
- 3.5.3 softmax 函数的特征
- 3.5.4 输出层的神经元数量
- 3.6 手写数字识别
- 3.6.1 MNIST 数据集
- 3.6.2 神经网络的推理处理
- 3.6.3 批处理
3.4 3 层神经网络的实现
3.4.1 符号确认
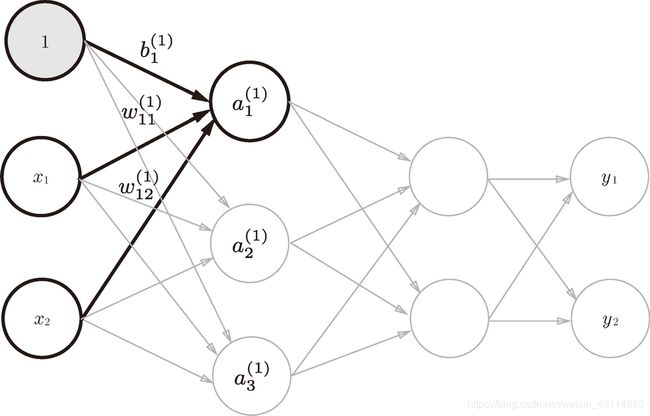
3.4.2 各层间信号传递的实现
- 任何前一层的偏置神经元“1”都只有一个。偏置权重的数量取决于后一层的神经元的数量(不包括后一层的偏置神经元“1”)
公式化:
a 1 ( 1 ) = w 11 ( 1 ) x 1 + w 12 ( 1 ) x 2 + b 1 ( 1 ) ( 1 ) a_1^{(1)}=w_{11}^{(1)}x_1+w_{12}^{(1)}x_2+b_{1}^{(1)} (1) a1(1)=w11(1)x1+w12(1)x2+b1(1)(1)
a 2 ( 1 ) = w 21 ( 1 ) x 1 + w 22 ( 1 ) x 2 + b 2 ( 1 ) ( 2 ) a_2^{(1)}=w_{21}^{(1)}x_1+w_{22}^{(1)}x_2+b_{2}^{(1)} (2) a2(1)=w21(1)x1+w22(1)x2+b2(1)(2)
a 3 ( 1 ) = w 31 ( 1 ) x 1 + w 32 ( 1 ) x 2 + b 3 ( 1 ) ( 3 ) a_3^{(1)}=w_{31}^{(1)}x_1+w_{32}^{(1)}x_2+b_{3}^{(1)} (3) a3(1)=w31(1)x1+w32(1)x2+b3(1)(3)
写成矩阵的格式:
( a 1 ( 1 ) a 2 ( 1 ) a 3 ( 1 ) ) = ( x 1 x 2 ) ∗ ( w 11 ( 1 ) w 21 ( 1 ) w 31 ( 1 ) w 12 ( 1 ) w 22 ( 1 ) w 32 ( 1 ) ) + ( b 1 ( 1 ) b 2 ( 1 ) b 3 ( 1 ) ) \begin{pmatrix} a_1^{(1)}\\ a_2^{(1)} \\a_3^{(1)} \end{pmatrix}= \begin{pmatrix} x_1&x_2\\ \end{pmatrix} *\begin{pmatrix} w_{11}^{(1)}&w_{21}^{(1)}&w_{31}^{(1)}\\ w_{12}^{(1)}&w_{22}^{(1)}&w_{32}^{(1)}\\ \end{pmatrix}+\begin{pmatrix} b_1^{(1)}\\ b_2^{(1)} \\b_3^{(1)} \end{pmatrix} ⎝⎜⎛a1(1)a2(1)a3(1)⎠⎟⎞=(x1x2)∗(w11(1)w12(1)w21(1)w22(1)w31(1)w32(1))+⎝⎜⎛b1(1)b2(1)b3(1)⎠⎟⎞
即:
A 1 = X ∗ W 1 + B 1 \boldsymbol{A_1}=\boldsymbol{X}*\boldsymbol{W_1}+\boldsymbol{B_1} A1=X∗W1+B1
- 其中 A 1 \boldsymbol{A_1} A1为第0层的所有神经元加权和偏置的和
- X \boldsymbol{X} X为第0层的所有神经元
- W 1 \boldsymbol{W_1} W1为第0层指向第1层的所有对应的权重
- B 1 \boldsymbol{B_1} B1为第0层的偏置对应第1层所有神经元
import numpy as np
X=np.array([1.0,2.0])
W1=np.array([[2.0,1.0,3.0],[1.0,3.0,2.0]])
B1=np.array([2.0,3.0,1.0])
A1=np.dot(X,W1)+B1
print(A1)
运行结果如下:
[ 6. 10. 8.]
- 节点 A 1 \boldsymbol{A_1} A1作为第0层加权和偏置的和
- 节点 Z 1 \boldsymbol{Z_1} Z1作为激活函数转换后的值
- 所以再将上面代码中计算出来的 A 1 \boldsymbol{A_1} A1代入激活函数sgimoid即可
def sigmoid(x):
return 1/(1+np.exp(-x))
...
Z1=sigmoid(A1)
print(Z1)
根据上面的一组数据得到的运行结果如下:
[0.99752738 0.9999546 0.99966465]
- 第 1 层到第 2 层的信号传递

公式化:
a 1 ( 2 ) = w 11 ( 2 ) z 1 + w 12 ( 2 ) z 2 + w 13 ( 2 ) z 2 + b 1 ( 2 ) ( 1 ) a_1^{(2)}=w_{11}^{(2)}z_1+w_{12}^{(2)}z_2+w_{13}^{(2)}z_2+b_{1}^{(2)} (1) a1(2)=w11(2)z1+w12(2)z2+w13(2)z2+b1(2)(1)
a 2 ( 2 ) = w 21 ( 2 ) z 1 + w 22 ( 2 ) z 2 + w 23 ( 2 ) z 2 + b 2 ( 2 ) ( 2 ) a_2^{(2)}=w_{21}^{(2)}z_1+w_{22}^{(2)}z_2+w_{23}^{(2)}z_2+b_{2}^{(2)} (2) a2(2)=w21(2)z1+w22(2)z2+w23(2)z2+b2(2)(2)
写成矩阵的格式:
( a 1 ( 2 ) a 2 ( 2 ) ) = ( z 1 z 2 z 3 ) ∗ ( w 11 ( 2 ) w 21 ( 2 ) w 12 ( 2 ) w 22 ( 2 ) w 13 ( 2 ) w 23 ( 2 ) ) + ( b 1 ( 2 ) b 2 ( 2 ) ) \begin{pmatrix} a_1^{(2)}\\ a_2^{(2)} \\\end{pmatrix}= \begin{pmatrix} z_1&z_2&z_3\\ \end{pmatrix} *\begin{pmatrix} w_{11}^{(2)}&w_{21}^{(2)}\\ w_{12}^{(2)}&w_{22}^{(2)}\\w_{13}^{(2)}&w_{23}^{(2)} \end{pmatrix}+\begin{pmatrix} b_1^{(2)}\\ b_2^{(2)} \\\end{pmatrix} (a1(2)a2(2))=(z1z2z3)∗⎝⎜⎛w11(2)w12(2)w13(2)w21(2)w22(2)w23(2)⎠⎟⎞+(b1(2)b2(2))
即:
A 2 = Z 1 ∗ W 2 + B 2 \boldsymbol{A_2}=\boldsymbol{Z_1}*\boldsymbol{W_2}+\boldsymbol{B_2} A2=Z1∗W2+B2
Z 2 = s i g m o i d ( A 2 ) \boldsymbol{Z_2}=sigmoid(\boldsymbol{A_2}) Z2=sigmoid(A2)
- 注意 W 2 W_2 W2和 B 2 B_2 B2的维度问题,可以在运算前用shape()函数检查
- 除了输入改变,其它与之前的代码一致
下面是实现代码:
...
W2=np.array([[0.05,0.02],[0.03,0.01],[0.02,0.01]])
B2=np.array([0.2,0.5])
print(Z1.shape)
print(W2.shape)
print(B2.shape)
A2=np.dot(Z1,W2)+B2
Z2=sigmoid(A2)
print(Z2)
运行结果如下:
[0.57441032 0.63180003]
4. 第 2 层到输出层的信号传递
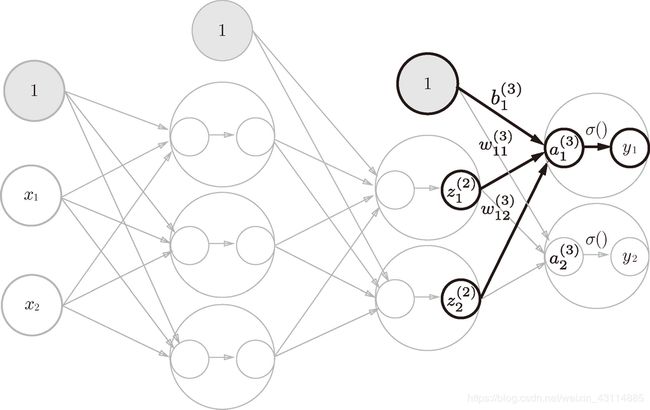
- 我们定义了identity_function() 函数(也称为“恒等函数”),并将其作为输出层的激活函数。恒等函数会将输入按原样输出,因此,这个例子中没有必要特意定义 identity_function()。
- 输出层的激活函数用 σ() 表示,不同于隐藏层的激活函数 h()(σ 读作 sigma)。
- 回归问题的输出层激活函数可以是恒等函数
- 二元分类问题输出层激活函数可以是sigmoid函数
- 多元分类问题输出层激活函数可以是softmax函数
实现代码如下:
def identity_function(x):
return x
...
W3=np.array([[0.6,0.7],[0.5,0.8]])
B3=np.array([0.5,0.5])
A3=np.dot(Z1,W2)+B3
Z3=identity_function(A3)
print(Z3)
运行结果如下:
[1.16054621 1.40752725]
3.4.3 代码实现小结
import numpy as np
def sigmoid(x):
return 1/(1+np.exp(-x))
def identity_function(x):
return x
def init_network(): #权重和偏置的初始化
network={} #定义了一个空列表
network['W1']=np.array([[2.0,1.0,3.0],[1.0,3.0,2.0]]) #只用大写字母表示权重
network['b1']=np.array([2.0,3.0,1.0])
network['W2']=np.array([[0.05,0.02],[0.03,0.01],[0.02,0.01]])
network['b2']=np.array([0.2,0.5])
network['W3']=np.array([[0.6,0.7],[0.5,0.8]])
network['b3']=np.array([0.5,0.5])
return network
def forward(network,x): #封装了将输入信号转换为输出信号的处理过程
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1=np.dot(x,W1)+b1
z1=sigmoid(a1)
print(z1)
a2=np.dot(z1,W2)+b2
z2=sigmoid(a2)
print(z2)
a3=np.dot(z2,W3)+b3
y=identity_function(a3)
return y
network=init_network() #字典变量network,保存了每一层所需的参数(权重和偏置)
x=np.array([1.0,2.0])
y = forward(network, x)
print(y)
3.5 输出层的设计
- 机器学习的问题大致可以分为分类问题和回归问题。
- 分类问题是数据属于哪一个类别的问题。比如,区分图像中的人是男性还是女性的问题就是分类问题。
- 回归问题是根据某个输入预测一个(连续的)数值的问题。比如,根据一个人的图像预测这个人的体重的问题就是回归问题(类似“57.4kg”这样的预测)。
3.5.1 恒等函数和 softmax 函数
- 转换处理用箭头表示
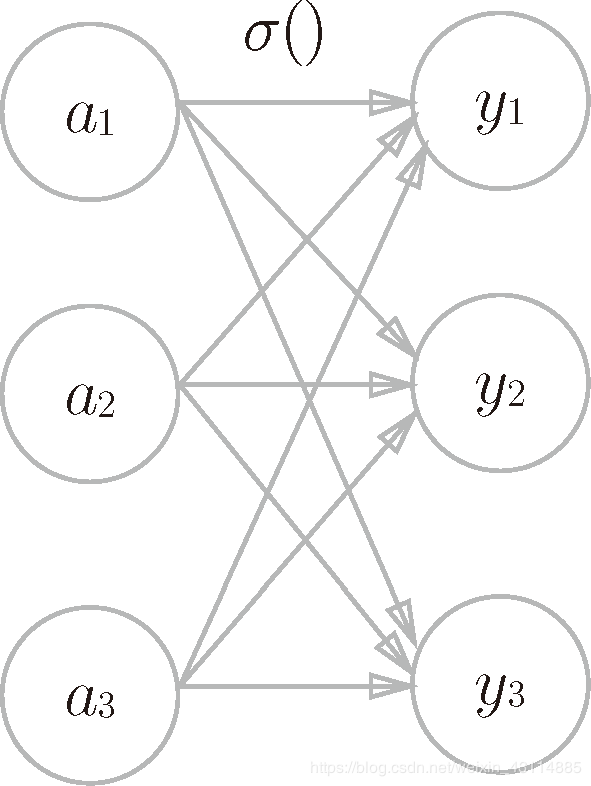
- softmax 函数
第k个神经元输出公式如下: y k = e a k ∑ i = 1 n e a i y_k=\frac{{\rm e}^{a_k}}{\sum_{i=1}^n{\rm e}^{a_i}} yk=∑i=1neaieak
a=np.array([0.3,2.9,4.0])
exp_a=np.exp(a)
print(exp_a)
sum_exp_a=np.sum(exp_a)
print(sum_exp_a)
y=exp_a/sum_exp_a
print(y)
运行结果如下:
[ 1.34985881 18.17414537 54.59815003]
74.1221542101633
[0.01821127 0.24519181 0.73659691]
定义softmax函数:
def softmax(a):
exp_a=np.exp(a)
sum_exp_a=np.sum(exp_a)
y=exp_a/sum_exp_a
return y
3.5.2 实现 softmax 函数时的注意事项
- 计算机处理“数”时,数值必须在 4 字节(32位)或 8 字节(64位)的有限数据宽度内。
- 指数函数的增长量很大,所以到infinity的时候,就会导致除法数值计算不确定的问题,即溢出问题。
为了解决该问题,变换softmax的公式如下:
y k = e a k ∑ i = 1 n e a i = C e a k C ∑ i = 1 n e a i = e ln C e a k ∑ i = 1 n e ln C e a i = e a k + ln C ∑ i = 1 n e a i + ln C y_k=\frac{{\rm e}^{a_k}}{\sum_{i=1}^n{\rm e}^{a_i}}=\frac{C{\rm e}^{a_k}}{C\sum_{i=1}^n{\rm e}^{a_i}}=\frac{{\rm e}^{\ln C}{\rm e}^{a_k}}{\sum_{i=1}^n{\rm e}^{\ln C}{\rm e}^{a_i}}=\frac{{\rm e}^{a_k+{\ln C}}}{\sum_{i=1}^n{\rm e}^{a_i+{\ln C}}} yk=∑i=1neaieak=C∑i=1neaiCeak=∑i=1nelnCeaielnCeak=∑i=1neai+lnCeak+lnC
= e a k + C ‘ ∑ i = 1 n e a i + C ‘ =\frac{{\rm e}^{a_k+C^`}}{\sum_{i=1}^n{\rm e}^{a_i+C^`}} =∑i=1neai+C‘eak+C‘ - 在进行 softmax 的指数函数的运算时, a i a^i ai加上(或者减去)某个常数并不会改变运算的结果
- 可以减去输入的最大值来防止溢出
a = np.array([1010, 1000, 990])
y=np.exp(a) / np.sum(np.exp(a)) # softmax函数的运算
print(y) # 没有被正确计算
c = np.max(a) # 1010
c = a - c #将每个元素值减小
print(c)
y=np.exp(c) / np.sum(np.exp(c))
print(y)
运行结果如下:
[nan nan nan]
[ 0 -10 -20]
[9.99954600e-01 4.53978686e-05 2.06106005e-09]
更改softmax函数:
def softmax(a):
c=np.max(a)
exp_a=np.exp(a-c)
sum_exp_a=np.sum(exp_a)
y=exp_a/sum_exp_a
return y
3.5.3 softmax 函数的特征
具体实现:
a = np.array([0.3, 2.9, 4.0])
y=softmax(a)
print(y)
sum=np.sum(y)
print(sum)
运行结果如下:
[0.01821127 0.24519181 0.73659691]
1.0
- softmax 函数的输出是 0.0 到 1.0 之间的实数
- softmax 函数的输出值的总和是 1
- softmax 函数输出可以作为概率,如:因为
y[2]=0.737(73.7%),概率最大,所以分类是第2个元素 - 因为即使用了 softmax 函数,各个元素之间的大小关系也不会改变,如第2个元素最大,作为分类结果的输出之中最大的也是第2个元素,而且指数函数的运算需要一定的计算机运算量,所以输出层的 softmax 函数一般会被省略
机器学习:分为学习和推理两个过程
学习:又称为“训练”,在这个过程中进行模型学习(使用训练数据,自动调整参数)
推理:用学到的模型对未知的数据进行推理(分类)
3.5.4 输出层的神经元数量
3.6 手写数字识别
- 推理处理:神经网络的前向传播(forward propagation)
3.6.1 MNIST 数据集
- MNIST 数据集是由 0 到 9 的数字图像构成的
- 训练图像有
6万张,测试图像有1万张 - MNIST 的图像数据是
28 像素 × 28 像素(784个像素点的灰度图像(1 通道),各个像素的取值在0 到 255之间。每个图像数据都相应地标有“7”“2”“1”等标签。
- 下载好课程自带的所有源代码后,dataset目录下有Python 脚本
mnist.py,该脚本支持从下载 MNIST 数据集到将这些数据转换成 NumPy 数组等处理。 - 在
jupiter notebook中打开mnist_show.py,并且运行,第一次运行因为调用dataset/mnist.py中的load_mnist函数会显示
Downloading train-images-idx3-ubyte.gz …,正在下载和读入mnist数据集,第 2 次及以后的调用只需读入保存在本地的文件(pickle 文件)即可,因此处理所需的时间非常短。
# coding: utf-8 # 声明编码方式为utf-8
import sys, os #引入python系统功能模块
sys.path.append(os.pardir) # #添加当前文件的上级目录的上级目录即【源代码】深度学习入门:基于Python的理论与实现到sys.path(Python 的搜索模块的路径集)
import numpy as np
from dataset.mnist import load_mnist #从dataset文件夹的mnist.py文件中添加load_mnist函数
from PIL import Image #从图像的显示 PIL(Python Image Library)模块中添加Image类
def img_show(img):
pil_img = Image.fromarray(np.uint8(img)) # 先将img转化为uint8(0-255无符号8位整型)数组,再将np.array类型的转换成PIL型数据
pil_img.show() #用PIL模块将image显示出来
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False) #将load_mnist读取出来的( 训练图像, 训练标签 ),( 测试图像, 测试标签 )形式的数据分别放到一维训练图像数组和一维测试图像数组中,且一维数组中数的大小,即图像像素是0-255
img = x_train[0] #取出第一个图像
label = t_train[0] #取出第一个图像的标签
print(label) # 5 #第一个图像是5
print(img.shape) # (784,) #第一个图像的形状(一维数组大小784大)
img = img.reshape(28, 28) # 把图像的形状变为原来的尺寸(28*28)
print(img.shape) # (28, 28)# 第一个图像表述形式变成了2维
img_show(img)
- load_mnist函数
- 返回( 训练图像, 训练标签 ),( 测试图像, 测试标签 )形式的mnist数据
- load_mnist(normalize=True, flatten=True, one_hot_label=False)
第 1 个参数 normalize 设置是否将输入图像正规化为 0.0~1.0 的值。如果将该参数设置为 False,则输入图像的像素会保持原来的 0~255
第 2 个参数 flatten 设置是否展开输入图像(变成一维数组)。如果将该参数设置为 False,则输入图像为 1 × 28 × 28 的三维数组;若设置为 True,则输入图像会保存为由 784 个元素构成的一维数组。
第 3 个参数 one_hot_label 设置是否将标签保存为one-hot表示(one-hot representation)。one-hot 表示是仅正确解标签为 1,其余皆为 0 的数组,就像 [0,0,1,0,0,0,0,0,0,0] 这样。当 one_hot_label 为 False 时,只是像 7、2 这样简单保存正确解标签;当 one_hot_label 为 True 时,标签则保存为 one-hot 表示。
调用完mnist_show.py后,训练图像的第一张就会显示出来

3.6.2 神经网络的推理处理
- 我们假设学习已经完成,所以学习到的参数被保存下来。假设保存在 sample_weight.pkl 文件中,在推理阶段,我们直接加载这些已经学习到的参数
- 此神经网络输入层有784(mnist数据集图片像素点个数一维数组个数)个神经元,第1个隐藏层有50个神经元,第2个隐藏层有100个神经元,输出层有10个神经元(0-9)
import pickle #引入pickle库
sys.path.append(os.pardir)
import numpy as np
from dataset.mnist import load_mnist
from PIL import Image
def img_show(img): #图像显示函数
pil_img = Image.fromarray(np.uint8(img))
pil_img.show()
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)
img = x_train[0]
label = t_train[0]
print(label) # 5
print(img.shape) # (784,)
img = img.reshape(28, 28) # 把图像的形状变为原来的尺寸
print(img.shape) # (28, 28)
img_show(img)
def sigmoid(x): #sigmoid函数
return 1/(1+np.exp(-x))
def softmax(a): #softmax函数
c=np.max(a)
exp_a=np.exp(a-c)
sum_exp_a=np.sum(exp_a)
y=exp_a/sum_exp_a
return y
def get_data(): #得到测试集数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
return x_test, t_test
def init_network(): #会读入保存在 pickle 文件 sample_weight.pkl 中的学习到的权重参数,因为之前我们假设学习已经完成
with open("sample_weight.pkl", 'rb') as f:
network = pickle.load(f) #将f文件中已经学习出来的权重参数放到字典变量中
return network
def predict(network, x): #mnist数据集,3层神经网络的向前传播
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1) #第1层激活函数
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2) #第2层激活函数
a3 = np.dot(z2, W3) + b3
y = softmax(a3) #输出层激活函数
return y
x, t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):
y = predict(network, x[i])
p = np.argmax(y) # 获取概率最高的元素的索引
if p == t[i]: #索引和标签相同表示分类正确
accuracy_cnt += 1
print("Accuracy:" + str(float(accuracy_cnt) / len(x))) #计算有多少百分比的数据被正确分类
运行结果如下:
5
(784,)
(28, 28)
Accuracy:0.9352
- 有 93.52 % 的数据被正确分类
- 对神经网络的输入数据进行某种既定的转换称为预处理(pre-processing)
- 各个像素值除以 255,进行了简单的正规化
- 利用数据整体的均值或标准差,移动数据,使数据整体以 0 为中心分布,或者进行正规化,把数据的延展控制在一定范围内
- 还有将数据整体的分布形状均匀化的方法,即数据白化(whitening)
3.6.3 批处理
- 现在我们来考虑打包输入多张图像的情形。比如,我们想用 predict() 函数一次性打包处理 100 张图像。
- 这种打包式的输入数据称为批(batch)。批有“捆”的意思,图像就如同纸币一样扎成一捆。
- 批处理对计算机的运算大有利处,可以大幅缩短每张图像的处理时间。那么为什么批处理可以缩短处理时间呢?这是因为大多数处理数值计算的库都进行了能够高效处理大型数组运算的最优化。
x, t = get_data()
network = init_network()
batch_size = 100 # 批数量
accuracy_cnt = 0
for i in range(0, len(x), batch_size): #range(start, end),start-end-1列表 range(start, end, step) 跨越step大小生成列表
x_batch = x[i:i+batch_size] #从i到i+批处理数量的数据取出,即本例中x[0:100]、x[100:200]
y_batch = predict(network, x_batch)
p = np.argmax(y_batch, axis=1) #axis=1表示行方向寻找概率最大元素的索引
accuracy_cnt += np.sum(p == t[i:i+batch_size])(把批处理的所有正确找到的数的数量相加)
print(float(accuracy_cnt))
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))(测试总数据总数据1万个,总共检测出9352)
运行结果如下
…
9001.0
9091.0
9172.0
9261.0
9352.0
Accuracy:0.9352
end
- 原书为《深度学习入门 基于Python的理论与实现》作者:斋藤康毅
人民邮电出版社 - 本文章是gitchat的《陆宇杰的训练营:15天共读深度学习》1的课程读书笔记
- 本文章大量引用原书中的内容和训练营课程中的内容作为笔记
《陆宇杰的训练营:15天共读深度学习》 ↩︎