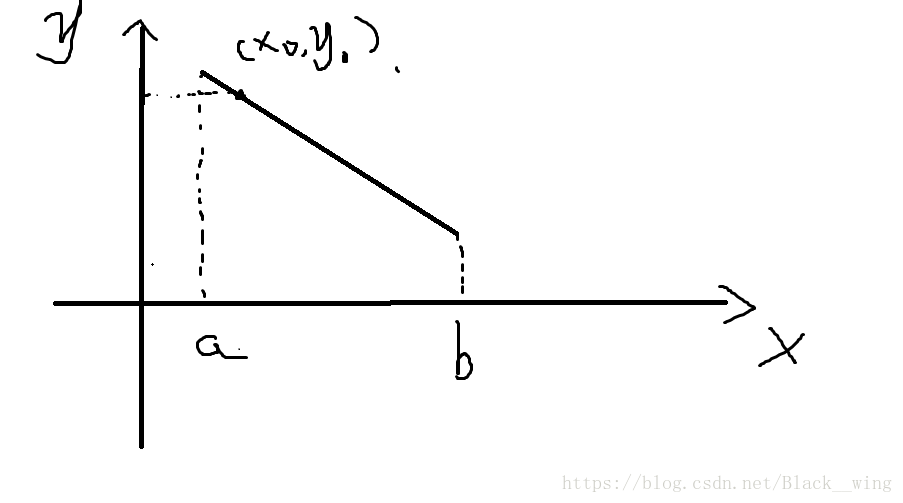二分答案总结&例题解析
对于二分我们最初的了解,就是在一个一次函数中,对于要求的点,(x,y)已知y,对于包含x值的区间二分,根据函数值与y比较,逐步靠近要求的点,直到最终求出要求的点。
在程序执行时,二分的时间复杂度为logn,可以极大的减少查找的时间。
二分的应用
严格来讲答案具有单调性的问题都可以用二分来解决,对于答案类似于一个一次函数,通过不断判断答案是否满足缩小区间。
1:求最大值中的最小值:
对所给区间进行二分,判断时,认为,时最大值中找最小的答案,所以这个答案如果比这个最小的答案要大,那么他也是可以成立的,它就可能是我们想要求得值,因此,在这给它做一个记录,ans=mid;这个答案最终的判断标准是很重要的。
例题:
洛谷p1182
将一个n个数组成的数列分成m段要求每段和的最大值最小:
将数组最小值跟最大值作为二分的左右值,贪心判断二分答案是否正确。
贪心过程大致为,对于可能存在的答案mid,将原数组相加,求得的值如果大于mid,cnt++,最后得到的cnt如果小于m,就说明我们取得这个最大值,大了(根据我们上面的分析,虽然它太大了,但它作为最大值而言是合乎提议的,因此,要使ans=mid),不是我们想要的最小值,那么我们就将它变小,并且使ans=mid。
#include
#include
#include
#include
using namespace std;
int n,m,a[100005];
int solve(int x)
{
int sum=0,cnt=0;
for(int i=0;i=m)
return 1;
else
return 0;
}
int main()
{
while(~scanf("%d%d",&n,&m))
{
int r=0,l=0,ans;
for(int i=0;i=l)
{
int mid = (r+l)/2;
if(solve(mid))
{
l=mid+1;
}
else
r=mid-1,ans=mid;
}
printf("%d\n",ans);
}
return 0;
}
2、最小值中的最大值,具体思路与1正相反:
例题:洛谷P1824
代码:
#include
#include
#include
#include
using namespace std;
const long long MAXN = 1e9;
int a[100005],n,c;
int solve(int dis)
{
int s=1;
int cnt =1;
for(int i = 2;i<=n;i++)
{
if(a[i]>=a[s]+dis)
{
s=i;
cnt++;
}
}
if(cnt>=c)
return 1;
else
return 0;
}
int main()
{
while(~scanf("%d%d",&n,&c))
{
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
sort(a+1,a+1+n);
int l,r,ans;
l=1,r=MAXN,ans =r;
while(l<=r)
{
int mid = (l+r)/2;
if(solve(mid))
{
ans = mid;
l=mid+1;
}
else
r=mid-1;
}
printf("%d\n",ans);
}
return 0;
}
3、平均值问题:
给一个长度为n的数列,需要找出一个序列的子串,求这个子串平均值最大是多少,子串长度>=m。
n<=1e5,我们来考虑一下这道题,如果我们求出每个子串,用线段树优化,时间复杂度最坏是logn*C(n,i)(i从1到n)的和,很明显。时间复杂度过高。我们再看,平均值,对于这个题来讲平均值的范围就在最小跟最大的数之间,并且具有单调性。
那么我们怎么解决这个问题?
我们思考如何构建solve函数能够判断这个找到的答案是否是我们想要的:
我们二分找到的是平均值,那么我们将数列所有的值,减去平均值,然后我们再构建一个前缀和序列,这样我们来看前缀和序列,如果存在一个i>j,使s[i]-s[j]>=0就说明这个值,可以作为平均值,这样我们的solve函数就构建完了。
代码:
#include
#include
#include
#include
using namespace std;
int n,m;
long long a[1000010],s[1000010],Min;
int solve(long long x)
{
s[0]=a[0]-x;
for(int i=1;i=m-1)
{
Min=min(Min,s[i-m]);
if(s[i]>=Min)
return 1;
}
}
return 0;
}
int main()
{
while(~scanf("%d%d",&n,&m))
{
long long maxn=0;
for(int i=0;i 4、noip2012借教室
这道题,对于申请天数进行二分,二分结果就是失败的那天。
那么solve函数如何构建?我们可以看到,这题是对于区间修改,单点求和的问题。对于x(包括x)前面的天数,进行区间修改,然后分别求出1-n天需要借的教室的数量,如果有一天需要借的数量大于,有的数量,那么这个人后面的人就不需要继续考虑了,只需要考虑这个人之前的人。
那么我们需要怎么维护这个区间,进行区间修改,单点求和。我能想到这么几种方法,线段树,树状数组,时间复杂度都是n*logn,但是,大佬说这种做法只能过90。可以直接用差分的方式解决:
差分对于一个区间i,j,对于第i个位置,加d,第j+1个位置减d,i的前缀和就代表了第i天的被借教室数。时间复杂度o(1)。
代码:
#include
#include
#include
using namespace std;
int n,m,num[1010000],d[1010000],sta[1010000],end[1010000],Q[1010000],L,R,ans;
bool check(int x)
{
int total=0;
for(int i=1;i<=n;++i)Q[i]=0;
for(int i=1;i<=x;++i)Q[sta[i]]+=d[i],Q[end[i]+1]-=d[i];
for(int i=1;i<=n;++i)
{
total+=Q[i];
if(total>num[i])return false;
}
return true;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i)scanf("%d",&num[i]);
for(int i=1;i<=m;++i)scanf("%d%d%d",&d[i],&sta[i],&end[i]);
L=1;R=m;
while(L<=R)
{
int mid=(L+R)>>1;
if(check(mid))L=mid+1;
else ans=mid,R=mid-1;
}
if(L>m)printf("0");
else printf("-1\n%d",ans);
return 0;
}
5、codeforce 923B
这一道题跟上一道几乎完全一样,二分判断这堆雪会在哪一天化掉,最后根据每天剩余多少堆雪判断,这一天化掉雪的总数。维护时是但点更新,区间求和,树状数组线段树都可,下面给出树状数组代码:
#include
#include
#include
#include
#include
#include
using namespace std;
#define ll long long
const int M=100005;
int v[M];
int t[M];
ll sum[M];
ll ans[M];
ll num[M];
int n;
void add(int p,ll x)
{
for(int i=p;i<=n;i+=i&-i)
sum[i]+=x;
}
ll ask(int p)
{
ll ans=0;
for(int i=p;i;i-=i&-i)
ans+=sum[i];
return ans;
}
int main()
{
while(~scanf("%d",&n))
{
for(int i=1;i<=n;i++)
{
scanf("%d",&v[i]);
}
for(int i=1;i<=n;i++)
{
scanf("%d",&t[i]);
add(i,t[i]);
}
for(int i=1;i<=n;i++)
{
int l=i,r=n,ansn=n+1;
while(l<=r)
{
int mid = (r+l)/2;
ll tmp = ask(mid)-ask(i-1);
if(tmp>v[i]) ansn=mid,r=mid-1;
else l=mid+1;
}
ans[ansn]+=v[i]-ask(ansn-1)+ask(i-1);
num[i]++;
num[ansn]--;
}
for(int i=1;i<=n;i++)
{
num[i]+=num[i-1];
printf("%lld ",num[i]*t[i]+ans[i]);
}
printf("\n");
}
return 0;
}