Python 中 Ridge 和 Lasso 回归的教程

作者：chen_h
微信号 & QQ：862251340
微信公众号：coderpai

---

线性回归和逻辑回归是回归技术中最受欢迎的技术，但是他们一般很难处理大规模数据问题，很难处理过拟合问题。所以，我们一般都会加上一些正则化技术，在本文中我们会介绍一些最基础的正则化技术，Ridge 回归和 Lasso 回归。这两种回归技术总体的思路是不变的。

1. 简要概述

Ridge 和 Lasso 回归是通常用于在存在大量特征的情况下创建简约模型的强大技术。这里的大数据指的是两方面：

• 大到模型足以会有过度拟合的趋势；
• 大到足以引起计算硬件挑战。对于现代系统，在数百万或者数十亿特征的情况下可能出现这种情况；

虽然 Ridge 和 Lasso 可能都朝着共同的目标努力，但固有属性和实际使用案例是非常不同的。如果你以前没有听过他们，那么你必须知道他们的作用就是惩罚系数的大小，同时最小化预测值与真实值之间的误差。这些都被称为正则化技术。他们之间的差别就在于如何对系数进行惩罚：

• Ridge 回归：
  • 执行 L2 正则化，即增加相当于系数幅度的平方的惩罚
  • 最小化目标函数：LS Obj + a*（系数平方和）
• Lasso 回归：
  • 执行 L1 正则化，即增加相当于系数幅度的绝对值的惩罚
  • 最小化目标函数：LS Obj + a*（系数绝对值之和）

注意：这里 LS Obj 指的是 最小二乘目标，即没有正则化的线性回归目标。

如果你对惩罚项和正则化这样的术语看起来很陌生，请不要担心我们会在本文的后续过程中更加详细的讨论这些内容。在升入研究他们如何工作之前，让我们试着弄清楚为什么惩罚系数的大小会起作用。

2. 为什么要惩罚系数的大小？

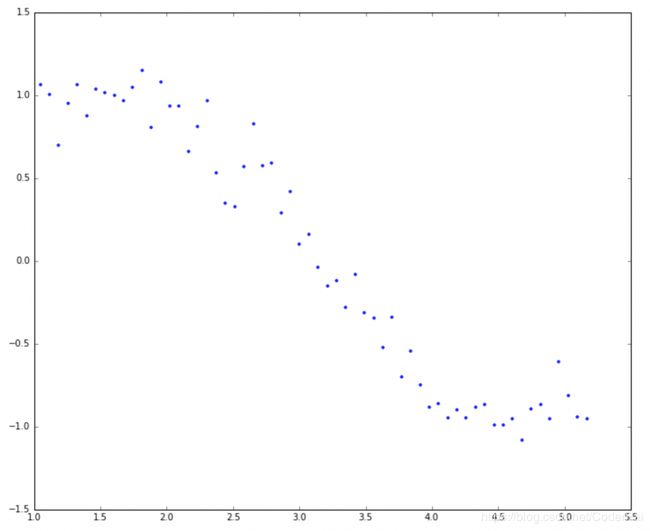
让我们试着理解模型复杂性对系数大小的影响。例如，我们模拟了正弦曲线（在 60° 和 300° 之间）并使用以下代码添加了一些随机噪声：

#Importing libraries. The same will be used throughout the article.
import numpy as np
import pandas as pd
import random
import matplotlib.pyplot as plt
%matplotlib inline
from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 12, 10

#Define input array with angles from 60deg to 300deg converted to radians
x = np.array([i*np.pi/180 for i in range(60,300,4)])
np.random.seed(10)  #Setting seed for reproducability
y = np.sin(x) + np.random.normal(0,0.15,len(x))
data = pd.DataFrame(np.column_stack([x,y]),columns=['x','y'])
plt.plot(data['x'],data['y'],'.')

这类似于正弦曲线但不完全是因为噪声。我们将以此为例来测试本文中需要的不同场景。让我们尝试使用 x 为 1 到 15 的幂的多项式回归来估计正弦函数。让我们在数据帧中为每个幂增加一列 15。这可以使用以下代码完成：

for i in range(2,16):  #power of 1 is already there
    colname = 'x_%d'%i      #new var will be x_power
    data[colname] = data['x']**i
print(data.head())

          x         y       x_2       x_3       x_4       x_5       x_6  \
0  1.047198  1.065763  1.096623  1.148381  1.202581  1.259340  1.318778   
1  1.117011  1.006086  1.247713  1.393709  1.556788  1.738948  1.942424   
2  1.186824  0.695374  1.408551  1.671702  1.984016  2.354677  2.794587   
3  1.256637  0.949799  1.579137  1.984402  2.493673  3.133642  3.937850   
4  1.326450  1.063496  1.759470  2.333850  3.095735  4.106339  5.446854   

        x_7       x_8        x_9       x_10       x_11       x_12       x_13  \
0  1.381021  1.446202   1.514459   1.585938   1.660790   1.739176   1.821260   
1  2.169709  2.423588   2.707173   3.023942   3.377775   3.773011   4.214494   
2  3.316683  3.936319   4.671717   5.544505   6.580351   7.809718   9.268760   
3  4.948448  6.218404   7.814277   9.819710  12.339811  15.506664  19.486248   
4  7.224981  9.583578  12.712139  16.862020  22.366630  29.668222  39.353420   

        x_14       x_15  
0   1.907219   1.997235  
1   4.707635   5.258479  
2  11.000386  13.055521  
3  24.487142  30.771450  
4  52.200353  69.241170  

现在我们拥有了所有 15 个幂，让我们来制作 15 个不同的线性回归模型，每个模型包含 x 从 1 到特定型号的变量。例如，模型 8 的特征集是 {x, x_2, x_3, x_4, x_5, x_6, x_7, x_8} 。

首先，我们将定义一个通过 函数，它接受 x 所需的最大幂作为输入，并返回一个包含 [ model RSS, intercept, coef_x, coef_x2, … upto entered power ] 的列表。这里 RSS 指的是 残差平方和，它只是训练数据集中预测值和实际值之间的误差平方和。定义该函数的 Python 代码如下：

#Import Linear Regression model from scikit-learn.
from sklearn.linear_model import LinearRegression
def linear_regression(data, power, models_to_plot):
    #initialize predictors:
    predictors=['x']
    if power>=2:
        predictors.extend(['x_%d'%i for i in range(2,power+1)])
    
    #Fit the model
    linreg = LinearRegression(normalize=True)
    linreg.fit(data[predictors],data['y'])
    y_pred = linreg.predict(data[predictors])
    
    #Check if a plot is to be made for the entered power
    if power in models_to_plot:
        plt.subplot(models_to_plot[power])
        plt.tight_layout()
        plt.plot(data['x'],y_pred)
        plt.plot(data['x'],data['y'],'.')
        plt.title('Plot for power: %d'%power)
    
    #Return the result in pre-defined format
    rss = sum((y_pred-data['y'])**2)
    ret = [rss]
    ret.extend([linreg.intercept_])
    ret.extend(linreg.coef_)
    return ret

请注意，此函数不会绘制所有幂的模型，但会返回所有模型的 RSS 和系数。我现在将跳过代码的细节，直接展示结果。现在，我们可以制作所有 15 个模型并比较结果。为便于分析，我们将所有结果保存在 pandas 数据框中，并绘制 6 个模型以了解趋势。请参考一下代码：

#Initialize a dataframe to store the results:
col = ['rss','intercept'] + ['coef_x_%d'%i for i in range(1,16)]
ind = ['model_pow_%d'%i for i in range(1,16)]
coef_matrix_simple = pd.DataFrame(index=ind, columns=col)

#Define the powers for which a plot is required:
models_to_plot = {1:231,3:232,6:233,9:234,12:235,15:236}

#Iterate through all powers and assimilate results
for i in range(1,16):
    coef_matrix_simple.iloc[i-1,0:i+2] = linear_regression(data, power=i, models_to_plot=models_to_plot)

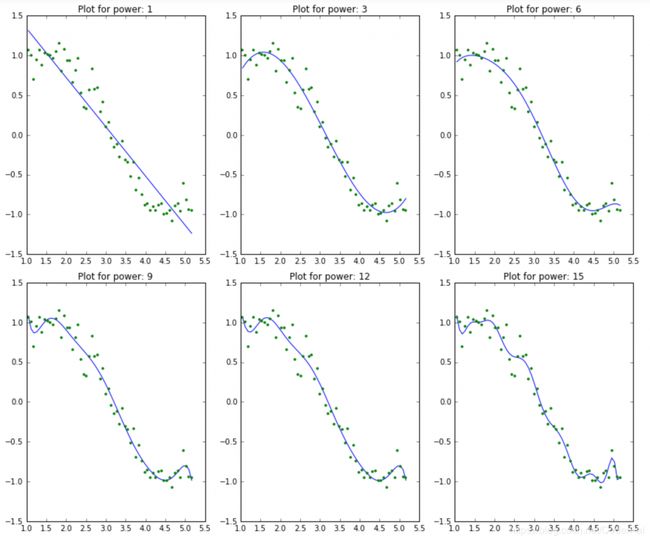
我们希望复杂度越来越高的模型能够更好的拟合数据并导致 RSS 值降低。这也可以通过查看 6 个模型生成的图来验证：

这清楚的符合我们最初的理解。随着模型复杂度的增加，模型倾向于在训练数据集中适应甚至更小的偏差。虽然这会导致过度拟合，但我们暂时搁置这个问题并达到我们的主要目标，即对系数大小的影响。这可以通过查看上面创建的数据框来分析。

#Set the display format to be scientific for ease of analysis
pd.options.display.float_format = '{:,.2g}'.format
coef_matrix_simple

很明显，随着模型复杂度的增加，系数的大小呈现指数增长。我希望这给出了一些直觉，为什么对系数的大小进行约束可能是降低模型复杂度的好主意。让我们试着更好的理解这一点。系数值很大表示什么？这意味着我们非常重视该特征，即特定特征是结果的良好预测因子。当他变得太大时，算法开始建模复杂关系以估计输出并且最终过度拟合到特定训练数据。

3. Ridge 回归

正如前面我们所了解的，Ridge 回归是采用了 L2 正则化，即它在优化目标中增加系数平方和的因子。因此，岭回归优化了以下内容：

Objective = RSS + α * (sum of square of coefficients)

这里，$\alpha$ 是平衡最小化 RSS 与最小化系数平方和的强调量的参数。$\alpha$ 可以采用不同的值：

• $\alpha =0$
  • 目标与简单线性回归相同。
  • 我们将获得与简单线性回归相同的系数。
• $\alpha =\infty$
  • 系数将为零。为什么？由于系数平方为无限权重，任何小于零的东西都会使目标无限。
• $0<\alpha <\infty$
  • $\alpha$ 的大小将决定给予目标的不同部分的权重。
  • 对于简单线性回归，系数将介于 0 和 1 之间。

我希望这能说明 $\alpha$ 如何影响系数的大小。有一点可以肯定的是，任何非零值都会给出小于简单线性回归的值。

首先，我们为 Ridge 回归定义一个通用函数，类似于为简单线性回归定义一个函数，Python 代码如下：

from sklearn.linear_model import Ridge
def ridge_regression(data, predictors, alpha, models_to_plot={}):
    #Fit the model
    ridgereg = Ridge(alpha=alpha,normalize=True)
    ridgereg.fit(data[predictors],data['y'])
    y_pred = ridgereg.predict(data[predictors])
    
    #Check if a plot is to be made for the entered alpha
    if alpha in models_to_plot:
        plt.subplot(models_to_plot[alpha])
        plt.tight_layout()
        plt.plot(data['x'],y_pred)
        plt.plot(data['x'],data['y'],'.')
        plt.title('Plot for alpha: %.3g'%alpha)
    
    #Return the result in pre-defined format
    rss = sum((y_pred-data['y'])**2)
    ret = [rss]
    ret.extend([ridgereg.intercept_])
    ret.extend(ridgereg.coef_)
    return ret

注意，这里使用的是 Ridge 函数，它需要 alpha 作为初始化参数。另外，请记住，对输入进行标准化通常是每种类型回归的必修课，所以我们在 Ridge 回归中也使用了。

现在，让我们分析 10 个不同 $\alpha$ 值对 Ridge 回归结果的影响，$\alpha$ 的值我们取 1e-15 到 20之间的 10 个值。这样我们就可以很容易的分析 $\alpha$ 值变化的趋势。然而，这些因具体场景而异。

请注意，这 10 个模型中的每一个都将包含所有 15 个变量，而且只有 $\alpha$ 的值会有所不同。这与简单的线性回归情况不同，其中每个模型都具有特征的子集。

Python 代码如下：

#Initialize predictors to be set of 15 powers of x
predictors=['x']
predictors.extend(['x_%d'%i for i in range(2,16)])

#Set the different values of alpha to be tested
alpha_ridge = [1e-15, 1e-10, 1e-8, 1e-4, 1e-3,1e-2, 1, 5, 10, 20]

#Initialize the dataframe for storing coefficients.
col = ['rss','intercept'] + ['coef_x_%d'%i for i in range(1,16)]
ind = ['alpha_%.2g'%alpha_ridge[i] for i in range(0,10)]
coef_matrix_ridge = pd.DataFrame(index=ind, columns=col)

models_to_plot = {1e-15:231, 1e-10:232, 1e-4:233, 1e-3:234, 1e-2:235, 5:236}
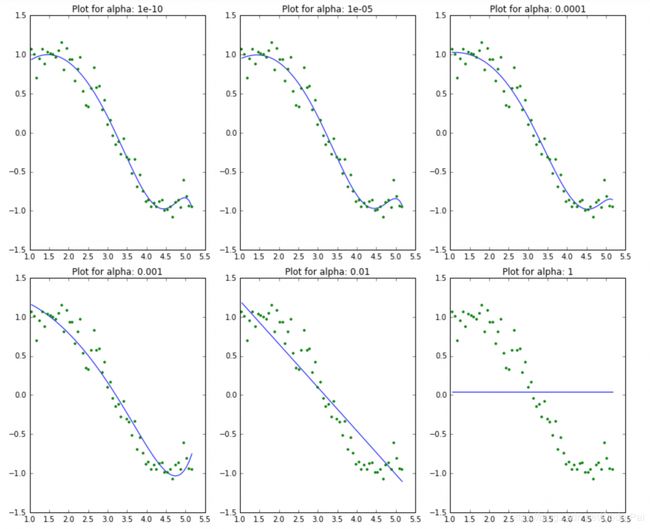
for i in range(10):
    coef_matrix_ridge.iloc[i,] = ridge_regression(data, predictors, alpha_ridge[i], models_to_plot)

在这里我们可以清楚的看到，随着 alpha 值的增加，模型复杂度降低了。虽然较高的 alpha 值会过拟合，但是显著较高的值也会导致欠拟合（例如 alpha=5）。因此，如何明智的选择 alpha 的值是至关重要的。一般我们会利用交叉验证来进行 alpha 值的选择，即 alpha 的值在一系列值上面进行迭代，并且选择给出较高交叉验证分数的值。

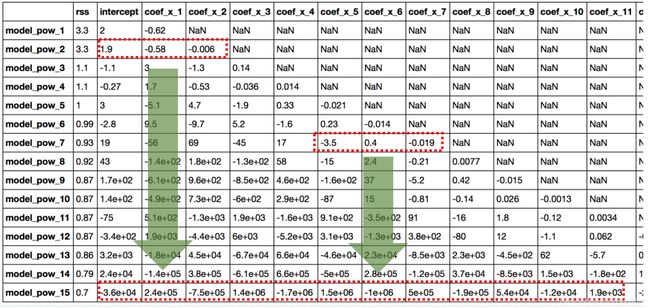
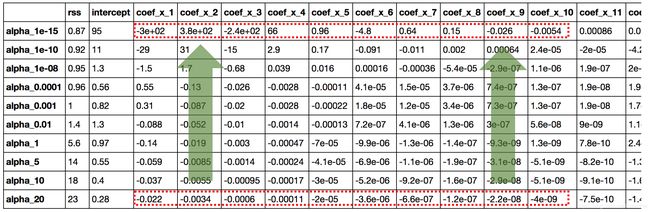
让我们看一下上面模型中系数的值：

#Set the display format to be scientific for ease of analysis
pd.options.display.float_format = '{:,.2g}'.format
coef_matrix_ridge

这里直接给出一些结论：

1. RSS 随着 alpha 的增加而增加，这种模型的复杂性降低了；
2. 小到 1e-15 的 alpha 使我们的系数幅度显著减小。将此表第一行中的系数与简单线性回归表的最后一行进行比较。
3. 高 alpha 值可能导致严重的不合适。请注意，对于大于 1 的alpha值，RSS会快速增加。
4. 虽然系数非常小，但是它们不能等于零。

前面三个结论都是非常直观的，但是第四个也是至关重要的。让我们通过确定系数数据集的每一行中的零个数来重新确认，Python代码如下：

coef_matrix_ridge.apply(lambda x: sum(x.values==0),axis=1)

alpha_1e-15     0
alpha_1e-10     0
alpha_1e-08     0
alpha_0.0001    0
alpha_0.001     0
alpha_0.01      0
alpha_1         0
alpha_5         0
alpha_10        0
alpha_20        0
dtype: int64

这证实了所有 15 个系数的幅度都大于零（可以是 +ve 或者 -ve）。记住这个观察结果再看一遍上面的结论就会非常清晰了。这将在后面比较 Ridge 回归和 Lasso 回归发挥重要作用。

4. Lasso 回归

Lasso 代表最小绝对收缩和选择算子。我知道它并没有给出太多的想法，但这里有两个关键词 —— ‘绝对’和‘选择’。

让我们先考虑前者，然后再担心后者。

Lasso 回归使用的是 L1 正则化，即它在优化目标中添加系数绝对值之和的因子。因此，Lasso 回归优化的是如下内容：

Objective = RSS + alpha*（系数绝对值之和）

这里，alpha 的工作原理跟 Ridge 中差不多，提供的也是平衡 RSS 和系数之间的大小。像 Ridge 回归那样，alpha 可以取各种值。让我们简单的在这边分析一下：

• alpha=0，与简单线性回归相同的系数
• $alpha=\infty$ ，所有系数为零（与之前逻辑一样）
• $0<alpha<\infty$ ，0与简单线性回归之间的系数

是的，到目前为止，它看起来跟 Ridge 非常相似。但是继续往下看，你就会发现这两者之间是有差异的。像以前一样，让我们对上面的问题设计一个 Lasso 回归。首先，我们来定义一个通用函数：

from sklearn.linear_model import Lasso
def lasso_regression(data, predictors, alpha, models_to_plot={}):
    #Fit the model
    lassoreg = Lasso(alpha=alpha,normalize=True, max_iter=1e5)
    lassoreg.fit(data[predictors],data['y'])
    y_pred = lassoreg.predict(data[predictors])
    
    #Check if a plot is to be made for the entered alpha
    if alpha in models_to_plot:
        plt.subplot(models_to_plot[alpha])
        plt.tight_layout()
        plt.plot(data['x'],y_pred)
        plt.plot(data['x'],data['y'],'.')
        plt.title('Plot for alpha: %.3g'%alpha)
    
    #Return the result in pre-defined format
    rss = sum((y_pred-data['y'])**2)
    ret = [rss]
    ret.extend([lassoreg.intercept_])
    ret.extend(lassoreg.coef_)
    return ret

注意 Lasso 函数中定义了的附加参数 -max_iter 。这是我们希望模型在不收敛的情况下运行的最大迭代次数。对于 Ridge 这个参数其实也是存在的，但是我们没有去修改。但是在这里我们对他进行修改了，将这个值设置为高于默认值了。为什么呢？下面的章节我会解释。

让我们使用 Python 代码来检查 10 个不同 alpha 值的输出：

#Initialize predictors to all 15 powers of x
predictors=['x']
predictors.extend(['x_%d'%i for i in range(2,16)])

#Define the alpha values to test
alpha_lasso = [1e-15, 1e-10, 1e-8, 1e-5,1e-4, 1e-3,1e-2, 1, 5, 10]

#Initialize the dataframe to store coefficients
col = ['rss','intercept'] + ['coef_x_%d'%i for i in range(1,16)]
ind = ['alpha_%.2g'%alpha_lasso[i] for i in range(0,10)]
coef_matrix_lasso = pd.DataFrame(index=ind, columns=col)

#Define the models to plot
models_to_plot = {1e-10:231, 1e-5:232,1e-4:233, 1e-3:234, 1e-2:235, 1:236}

#Iterate over the 10 alpha values:
for i in range(10):
    coef_matrix_lasso.iloc[i,] = lasso_regression(data, predictors, alpha_lasso[i], models_to_plot)

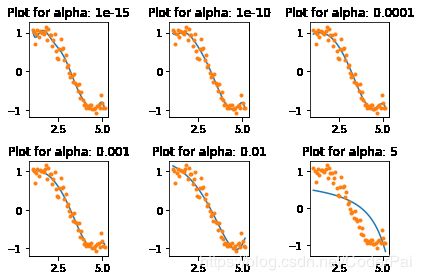
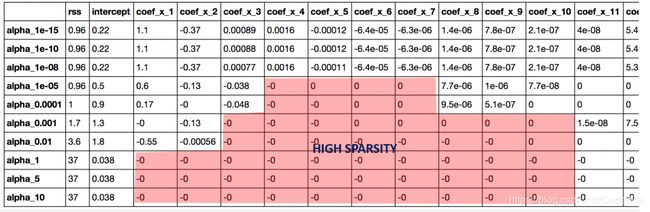
这个图再次告诉我们，模型复杂度随着 alpha 值的增加而降低。但请注意 alpha = 1 处的直线。让我们通过查看系数来进一步探索，Python 代码如下：

#Set the display format to be scientific for ease of analysis
pd.options.display.float_format = '{:,.2g}'.format
coef_matrix_lasso

除了对更高的 alpha 有更高的 RSS 的预期结论之外，我们还可以得到以下内容：

• 对于相同的 alpha 值来说，Lasso 回归的系数要比 Ridge 回归的系数小很多；
• 对于相同的 alpha 值来说，Lasso 回归比 Ridge 回归拥有更高的 RSS，说明拟合效果更差；
• 即使对于非常小的 alpha 值，许多系数也为零

结论 1 和结论 2 可能不会一直成立，因为有时候数据会有点不同，但是在大多数情况下是成立的。与 Ridge 回归真正的区别在于最后一条。让我们使用以下代码来检查每个模型中零的系数数量：

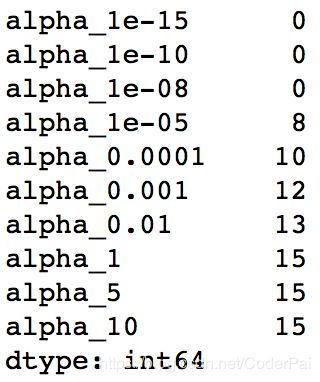
coef_matrix_lasso.apply(lambda x: sum(x.values==0),axis=1)

我们可以观察到即使对于非常小的 alpha 值，大量的系数也是零。这也解释了 Lasso 回归中当 alpha=1 时发生的水平线拟合，它瞬间变成了一个基线模型！大多数系数为零的这种线性称为“稀疏性”。虽然 Lasso 执行特征选择，但这种稀疏程度仅在特殊情况下实现，我们将在最后讨论。

与 Ridge 回归相比，这对 Lasso 回归的用例有一些非常有趣的影响。但是在进行最后的比较之前，让我们先看看这背后的数学观点，为什么系数在 Lasso 回归的时候回变成零，但是在 Ridge 回归的时候不会变成零。

5. 统计学说明

我个人比较喜欢曲线后面的数学基础，或者说是统计学基础，如果你不喜欢可以跳过这一章，如果你感兴趣你可以看一下 The Elements of Statistical Learning 这本书。但我个人认为，从长远来看，了解事物运作最本质的原理总会有好处的。

废话不多说，接下来，我们首先回顾一下回归问题中数据的基本结构。

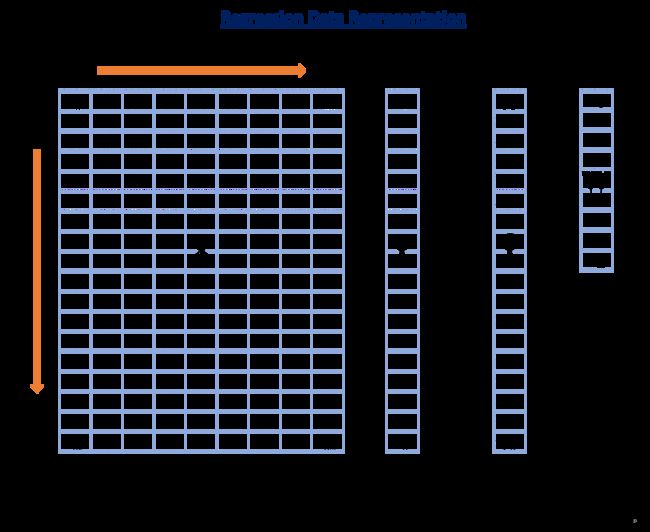
在上图中，你可以看到有四个数据元素：

• X：输入特征矩阵（nrow：N，nclo：M+1）
• Y：实际正确结果变量（维度：N）
• $\hat{Y}$：Y 的预测值（维度：N）
• w：权重或者系数（维度：M+1）

这里，N 是可用数据点的总数，M 是特征的总数。由于 M 特征和 1 个截距，所以 X 具有 M+1 列。

任何数据点 i 的预测结果是：

${\hat{y}}_i={\sum }_{j=0}^M{w}_j\ast x_{ij}$

它只是每个数据点的加权和，系数作为权重。通过基于某些标准找到权重的最佳值来实现该预测，这取决于所使用的回归算法的类型。让我们考虑所有 3 个案例：

1. 简单线性回归

要最小化的目标函数（也称为成本函数）仅是 RSS，即与实际结果相比的预测结果的平方误差之和。这可以在数学上描述为：

$Cost(W)=RSS(W)={\sum }_{i=1}^N(y_i-{\hat{y}}_i{)}^2={\sum }_{i=1}^N(y_i-{\sum }_{j=0}^M{w}_j{x}_{ij}{)}^2$

为了最小化这种成本，我们通常使用 “梯度下降” 算法。我现在不会详细介绍细节，但你可以参考一下。整体算法的工作原理如下：

1. initialize weights (say w=0)
2. iterate till not converged
   2.1 iterate over all features (j=0,1...M)
       2.1.1 determine the gradient
       2.1.2 update the jth weight by subtracting learning rate times the gradient
             w(t+1) = w(t) - learning rate * gradient

这里最重要的一步是 2.1.1 ，我们如何计算梯度。梯度只是成本相对于特定权重的偏微分（表示为 $W_j$），第 j 个权重的特度为：

步骤 #2.1.2 涉及使用渐变更新权重。简单线性回归的更新步骤如下所示：

我们可以使用渐变值进行检查。如果梯度足够小，则意味着我们非常接近最优，并且进一步的迭代将不会对系数产生实质性影响。可以使用 tol 参数更改渐变的下限。

让我们仙子阿考虑 Ridge 回归的情况。

2. Ridge 回归

要最小化的目标函数是 RSS 加上权重大小的平方和。这可以在数学上描述为：

在这种情况下，梯度计算公式为：

再次在梯度的正则化部分中，只有 $w_j$ 保持不变而其他都将变为零。相应的更新规则为：

在这里我们可以看到权重更新的第二部分与简单线性回归的第二部分相同。因此，Ridge 回归相当于首先将权重减小 （1-2λη）因子，然后应用与简单线性回归相同的更新规则。我希望这能给出一些直觉感受，说明为什么系数会减小到很小但从不变成零。

注意，在这种情况下收敛的标准仍然类似于简单的线性回归，即检查梯度的值。接下来，让我们讨论一下 Lasso 回归。

3. Lasso 回归

要最小化的目标函数是 RSS 加上权重大小的绝对值之和，这可以在数学上描述为：

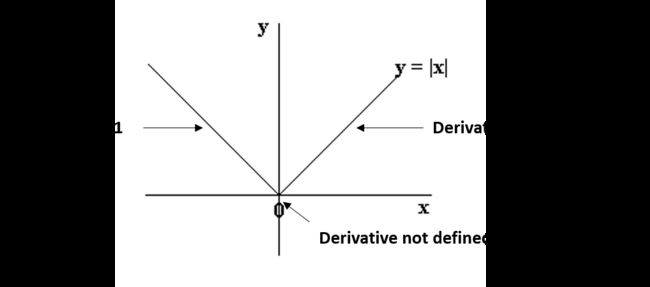
在这种情况下，因为绝对值函数在值等于 0 的情况下是不可微分的，所有我们修改公式为：

我们可以看到 0 的左侧和右侧的部分是具有定义的导数的直线，但是在 x=0 的时候无法区分该函数。在这种情况下，我们必须使用一种称为坐标下降的不同技术，该技术基于子梯度的概念。其中一个坐标下降遵循以下算法（这也是 sklearn 中的默认算法）：

1. initialize weights (say w=0)
2. iterate till not converged
   2.1 iterate over all features (j=0,1...M)
       2.1.1 update the jth weight with a value which minimizes the cost

步骤 2.1.1 看起来非常笼统，但是你值得拥有。

这里 $g(w_{-j})$ 代表（但不完全）实际结果与预测结果之间的差异，除了第 j 个变量之外的所有结果。如果该值很小，则意味着即使没有第 j 个变量，算法也能够很好的预测结果，因此可以通过设置领系数从等式中去除它。这给了我们一些直觉，说明为什么在 Lasso 回归的情况下系数变为零。

在坐标下降中，检查收敛是另一个问题。由于未定义渐变，我们需要另一种方法。存在许多替代方案，但最简单的方法是检查算法的步长。我们可以检查所有特征权重（上述算法的 #2.1 ）的任何特定周期中权重的最大差异。

如果这低于指定的 tol ，算法将停止。收敛速度不如梯度下降那么快，如果出现警告，表示算法在收敛前停止，我们可能必须设置 max_iter 参数。这就是我在 Lasso 泛型函数中指定此参数的原因。

让我们通过使用以下可视化比较所有三种情况中的系数来总结我们的理解，其显示了 Ridge 回归和 Lasso 回归与简单线性回归情况相比如何表现。

从上面的图中，我们可以发现：

• Ridge 回归系数是简单线性回归系数的减小因子，因此从不获得零值但是非常小的值；
• Lasso 回归系数在一定范围内变为零并且以恒定因子减小，这解释了与 Ridge 回归低的幅度；

在我们进一步学习之前，Lasso 回归和 Ridge 回归的另一个重要问题是截距问题。

现在，让我们来看看我们比较 Ridge 回归和 Lasso 回归在哪里使用。

6. 结论

现在我们对 Ridge 回归和 Lasso 回归的工作方式有了一个很好的了解，让我们试着通过比较他们来巩固我们的理解，并尝试欣赏它们的具体用例。我们还将他们与一些替代方法进行比较。我们从下面三个方面进行分析：

1. 关键差异

• Ridge：它包括模型中的所有特征。因此，Ridge 回归的主要优点是系数收缩和降低模型复杂性。
• Lasso：随着系数的缩小，Lasso 也会执行特征选择。正如我们之前观察到的那样，一些系数恰好为零，这相当于从模型中排出的特定特征。

传统上，逐步回归等技术用于执行特征选择并制作简约模型。但随着机器学习的进步，Ridge 回归和 Lasso 回归提供了非常好的选择，因为它们提供了更好的输出，需要更少的调整参数并且可以在很大程度上自动化。

2. 典型用例

• Ridge：它主要用于防止过度拟合。由于它包含了所有功能，因此在数百万的超级特征量的情况下它并不是非常有用，因为它会带来计算挑战；
• Lasso：由于它提供系数解决方案，它通常适用于建模数百万或者更多特征的模型。在这种情况下，获得系数解决方案具有很大的计算优势，因为可以简单的忽略具有零系数的特征。

不难看出为什么逐步选择技术在高纬情况下实现变得非常麻烦。因此，Lasso 提供了显著优势。

3. 存在高度相关的特征

• Ridge：即使存在高度相关的特征，它通常也能很好的工作，因为它将包括模型中的所有特征，但系数将根据相关性分布在它们之间。
• Lasso：它任意选择高度相关的任何一个特征，并将其余的系数减少到零。此外，所选变量随模型参数的变化而随机变化。与 Ridge 回归相比，这通常不能很好的起作用。

在我们上面的讨论中，可以观察到 Lasso 这个缺点。由于我们使用多项式回归，因此变量高度相关。如果不知道，可以查看 data.corr() 输出。因此，我们看到甚至小的 alpha 值都给出了显著的稀疏性，即 高 #coefficients 等于 0。

与 Ridge 回归和 Lasso 回归相似的，还有一个称为弹性网络回归，它将 L1 和 L2 正则都用起来了。

总结

在本文中，我概述了使用 Ridge 回归和 Lasso 回归的正则化。然后，我专注于惩罚系数大小的原因应该给我们简约的模型。接下俩，我们进入了 Ridge 回归和 Lasso 回归的细节，并看到了他们优于简单线性回归的优势。我们对他们为什么应该工作以及它们如何工作有一个直觉认识。

正则化技术非常有用，我鼓励你多用用。