线性时间复杂度排序
前言
我的博客之所以叫做“总理同学的暴力编程尝试…”说来话长。在我无数次的暴力编程尝试中,其中有一次就是给500万个整数进行排序,快排还有归并排序显然是卡爆了。快排一直在运转没有头,而归并排序直接就RE程序崩溃了。后来我听说了一种叫做“计数排序”的排序方式,得到了令我十分惊讶的成果,我用了4秒钟生成了500万个随机数,而给这些随机数排序却只用了3秒钟。因此怀着对“线性时间发杂度排序”的敬仰之情,写了这篇文章。
1.计数排序
计数排序是一个非基于比较的排序算法,该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时,它的复杂度为Ο(n+k)(其中k是整数的范围),快于任何比较排序算法。——360百科
计数排序不同于“快排”和“归并排序”等其他许多排序,其他的排序都是基于“数字之间的比较”而计数排序是基于“对数字的统计”。举一个最显著的例子:“冒泡排序”。冒泡排序的一生都致力于对两个数的比较,然后根据比较的结果对两个数进行交换。
在计数排序中,我们定义了一个数组“cnt”用来统计要排序的序列中每一个数字出现的次数,cnt[i]表示数字“i”出现的次数,我们先让s数组中的所有元素都初始化成“0”,然后把序列中的每一个数在数组中对应的位置加一,这样就统计出了每个数字在序列中出现的次数。然后从小到大看cnt,cnt[i]=0就说明“i”在原序列中没有出现过;cnt[i]!=0则说明“i”在原序列中出现过,把“cnt[i]”个“i”入队。因为我们令“i”从小到大变化,这就保证了先入队的数一定比后入队的数字要小,这样就实现了对原序列的排序。
代码如下:
int cnt[MaxM]={};//统计数组
void Csort(int* a,int n)//a为原数组,n为原数组的长度(给区间[1,n]进行排序)
{
memset(cnt,0,sizeof(cnt));//初始化数组
for(int i=1;i<=n;i++)
cnt[a[i]]++;//把a[i]的统计数加一
int aPos=1;//记录当前的"对尾"
for(int i=1;i<=1048575;i++)//对每一个可能出现的数字i
for(int k=1;k<=cnt[i];k++)//向队列中加入cnt[i]个数字i
a[aPos++]=i;//i入队
}但是上面的那段代码只能实现数字范围为0~MaxM-1的排序,因为cnt数组的大小为MaxM。如果我要实现对数字范围为-100~100的一组数进行排序呢?我们可以在统计时给每个数的身上都加上100,这样原序列的数字范围就变成了0~200,然后用上文同样的方法进行统计。在把cnt数组中数据存回原数组时再把我加上去的“100”减掉,之后再存回数组就可以了。
int cnt[201]={};//统计-100~100的所有数
void Csort(int* a,int n)
{
memset(cnt,0,sizeof(cnt));
for(int i=1;i<=n;i++)
cnt[a[i]+100]++;//用cnt[a[i]+100]表示数字a[i]出现的次数
int aPos=1;
for(int i=1;i<=1048575;i++)
for(int k=1;k<=cnt[i];k++)//所以cnt[i]表示的就是数字"i-100"出现的次数
a[aPos++]=i-100;
}因为计数排序是依靠cnt数组统计每一个数字出现的次数,所以cnt数组的大小要通过数据范围决定。如果数字的范围非常大,那么cnt就需要定义地很大,这样就会浪费很多空间。假设一种极端情况这个顺序列为a[]={0,1,10000000},用“冒泡排序”能够瞬间完成,但用“计数排序”则必须把cnt[0]~cnt[100000000]中的所有位置都看一遍。这也就说明:计数排序更适用于“小范围”的“大量数据”排序。
2.基数排序
基数排序(radix sort)属于”分配式排序”(distribution sort),又称”桶子法”(bucket sort)或bin sort,顾名思义,它是透过键值的部份资讯,将要排序的元素分配至某些”桶”中,藉以达到排序的作用,基数排序法是属于稳定性的排序,其时间复杂度为O (nlog(r)m),其中r为所采取的基数,而m为堆数,在某些时候,基数排序法的效率高于其它的稳定性排序法。——360百科
我保留对上述定义的看法。
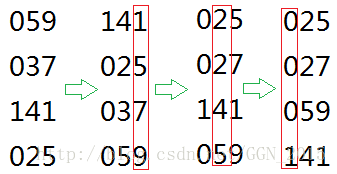
“基数排序”是一种在卡片排序机上实现的算法,在计算机上我们可以把它看做是对计数排序的一种改进算法。相比于计数排序,“计数排序”在时间上稍有逊色,但是在空间上却省了不少。“基数排序”的排序原理就是把所有的数拆成一个一个的十进制位,先把这些数按照个位上的数从小到大排序,再按照十位拍,再按照百位…直到每个数字的位置不再发生改变,排序就完成了。就像这样:
(请打开脑洞,然后再看下面一段话。)
简单地证明一下:我们先按照个位对所有数排序,然后再按十位对所有数排序。这时,对于十位相同的数,它们一定是按照个位从下到大排序的。然后我们再取排序它们的百位,一直排序到最大数的最高十进制位,这时所有的数就都得到正确的排序了。
这样讲可能不是很好理解,那就想象一个情景:假设你在给你的电脑中的一大堆DOC文件进行排序,你可以按照“文件建立时间”,“文件修改时间”,“文件大小”以及“文件名字典序”进行排序。如果我想按照“文件建立时间”,如果“文件建立时间”相同的按照“文件修改时间”排序。但是电脑上只有按照单一一项属性进行排序的功能,我想要实现多项属性进行排序,就得“一个一个”属性进行排序。先按照“文件修改时间”排序,然后再按照“文件建立时间”排序,这样就实现了我想要的功能。这其实就是一个“属性优先级”的问题,优先级低的先排,优先级高的后排,就可以实现。
而对于一个(带前导零的)整数来说,如果最高位上的数字大的数一定比最高位上小的数要大,而最高位相同的数我们又要通过次高位进行排序…最高位的优先级是最高的,最低位也就是个位的优先级是最低的。所以我们可以把每一个数的每一个十进制位上的数字当成是一种属性,然后先按照低位排序,再按照高位排序,这样就能到我想要的序列了。
代码如下:
long long ten[11]={1,10,100,1000,10000,100000,1000000,10000000,100000000,1000000000,10000000000LL};
//表示10的n次方
#define getNum(base,time) (base/ten[time])%10//得到一个数的当前十进制位
#define divTime(base,time) (base/ten[time])//求一个数除以10的time次方的结果(用来判断最高十进制位)
int s[10][MaxLen]={};//s[i][k]表示当前十进制位为i的第k个数
int Rsort(int* a,int n)//a为原数组,n为序列长度
{
int maxN=a[1];
for(int i=2;i<=n;i++)
maxN=max(maxN,a[i]);//找到最大的数
int cnt[10]={};//cnt[i]表示当前位为i的数的个数
for(int i=0;divTime(maxN,i)!=0;i++)//divTime(maxN,i)!=0表示最大的数在当前十进制位以上还有数
{
memset(cnt,0,sizeof(cnt));//初始化cnt数组
for(int j=1;j<=n;j++)
{
int numNow=getNum(a[j],i);//numNow当前数的当前数位
cnt[numNow]++;
s[numNow][cnt[numNow]]=a[j];//当前数字入放进"桶"中
}
int aPos=1;
for(int j=0;j<10;j++)
for(int k=1;k<=cnt[j];k++)
a[aPos++]=s[j][k];//再把桶中的数取出放回原数组
}
}[2018.2.2]写了另一个版本的基数排序,这个版本貌似更好一些。后缀数组的倍增算法就是利用了这种排序思想。
我们用count[i]表示权值小于等于i的所有元素的个数,按当前权值排序后,权值i最后一次出现的位置一定是count[i],同理权值i倒数第二次出现的位置一定是count[i]-1。这样我们可以从后向前扫一遍数组,每次把当前元素(假设它的权值是i)放到count[i]里,然后让count[i]–。得到的结果就是按权值排序后的结果(权值相同的按照原序排序)。
#include [2018.2.2]补记结束。
这就是基数排序的实现。
3.后记
计数排序是我见过最快的算法,当然也是一个拿空间换时间的“模范”,但是用的时候一定要谨慎。而基数排序对空间的要求就没有那么大了,只需要10*MaxLen的空间就可以保证不会“非法调用”。基数排序的思想还被应用到了后缀数组的计算中,非常的抽象。对基数排序没有深刻理解的同学可能在学习后缀数组是就会面临非常大的困难。