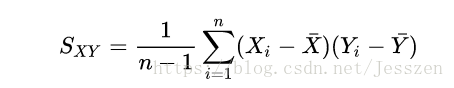【统计学习1】方差、协方差、相关系数与向量内积

第一：方差

定义：随机变量或者一组数据离散情况的度量。

为啥分母 n-1？

• a、目的：方差的估计是无偏的。
• b、原因：实际工作中，总体均数难以得到时，只能应用样本统计量代替总体参数。
• c、解释：分子上求期望【理解为求样本均值】已经用掉所有的自由度n；
•                事实上，如果分母n，因为第n个数，已经由n-1个数，和期望决定了，所有其没有信息量，所有要n-1。
•                简单说了，分子的期望，用掉了一个自由度。

第二：协方差

定义：在概率论和统计学中用于衡量两个变量的总体误差。

          而方差是协方差的一种特殊情况，即当两个变量是相同的情况。

• 方差：   Var(X)    = E[ (X-E(X)) *  (X-E(X)) ]
• 协方差：Cov(X,Y)= E[ (X-E(X))  *  (Y-E(Y)) ]

以上两个显然相似，方差就是协方差的特殊情况。

• 协方差为+，说明两个变量正相关。
• 协方差为-， 说明两个变量负相关。

***************************************************************************************************************************

观察一下公式。如果你认为x和y是正相关，那么你会expect x大于平均数的时候y也大于平均数，这就造成了x-EX与y-Ey相乘的每一项为正，加和也为正。所以如果协方差大于零，反应x与y正相关

***************************************************************************************************************************

第三：相关系数

定义：相关关系是一种非确定性的关系，相关系数是研究变量之间线性相关程度的量。

X、Y的协方差除以X的标准差和Y的标准差。

可以这样理解：相关系数是，剔除两个变量 量纲的影响，标准化后的’协方差‘。

特征：消除了两个变量变化幅度的影响，而只是单纯反应两个变量每单位变化时的相似程度。

值域：【-1，1】

显然，当变量x和变量y相同时，协方差=方差，p为1。

**************************************************************************************************************************

   知乎上标准化协方差的解释

   协方差：Cov(X,Y)= E[ (X-EX)  *  (Y-EY) ]

*************************************************************************************************************************

第四：余弦度量距离=相关系数？

==========================================================================

背景知识

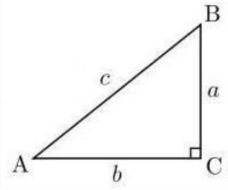
1、余弦

cosA = 临边/斜边  = b/c。

2、余弦第二定理【证明很简单】

3、向量点积【降级，得到一个标量】

两个向量 a =  [X1, X2,…, Xn]

              b = [Y1, Y2,…, Yn]

点积定义为：a·b=X1Y1+X2Y2+……+XnYn。

点积的几何解释：向量a在向量b上的投影长度，乘以b的模。

4、设向量a，b的夹角θ。

a·b = |a| × |b| × cosθ 【证明】

变形：cosθ =(a・b)/|a||b|

5、内积空间【又称欧几里得空间】

在一个有限维的向量空间，私人定制一个运算规则，如果我们定义了内积运算规则，那么这个空间，称为内积空间。

内积空间比向量空间多一种运算，就会多很多数学工具。

百度百科定义：

在数学上，内积空间是增添了一个额外的结构的矢量空间。这个额外的结构叫做内积或标量积。这个增添的结构将一对矢量与一个纯量连接起来，允许我们严格地谈论矢量的“夹角”和“长度”，并进一步谈论矢量的正交性。

==========================================================================

由相关系数定义，得到其主要目的是研究变量之间相关程度。

展开一下，我们也可以用“距离”，来衡量两个变量的相关性。

假设：两组变量a，b，将各自参数排成一排，就可以看作两个向量a，b。

在这个n空间，也就是我们定义内积运算得到内积空间中。

1、空间由两个向量，我们怎么定义其距离或者是相关性？

     自然想到向量的夹角，夹角大，则距离大，夹角小，则距离小。

2、怎样计算夹角？

     cosθ =(a・b)/|a||b|

    点积容易计算，向量的模也好计算。

3、参考相关系数公式

    

    

     夹角公式：  cosθ =(a・b)/|a||b|

     分子就是点积：X1Y1+X2Y2+……+XnYn

     分母就是向量a，b的模。

     cosθ =   E(XY)

                  /(E[X]*E[Y])

     根号不会打，分母需要根号，因为求的是向量模。

4、计算夹角的限制条件？

     1、因为根据协方差公式Cov(X,Y)= E[ (X-EX)  *  (Y-EY) ]，需要每个参数各自减掉均值.

          而向量a，b的点积=E[XY]=X1Y1+X2Y2+……+XnYn           并没有减掉均值，

     2、在根据相关系数公式，协方差/各自标准差，

           向量a，b的模也没有减掉均值。

     所以，在计算cosθ，先要将向量a，b进行均值化。