（4）聚类算法之OPTICS算法

1.引言

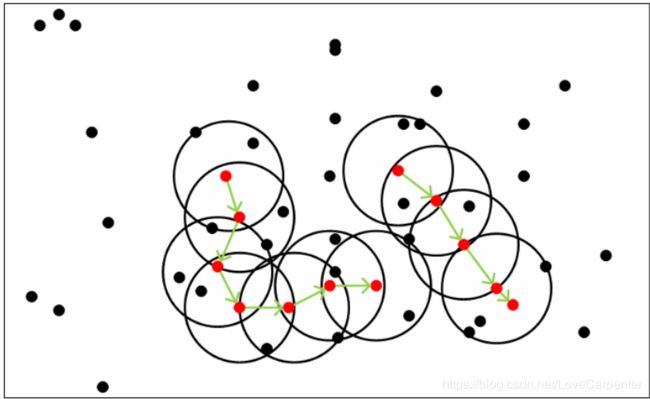
       OPTICS(Ordering points to identify the clustering structure)是一基于密度的聚类算法，OPTICS算法是DBSCAN的改进版本，因此OPTICS算法也是一种基于密度的聚类算法。在DBCSAN算法中需要输入两个参数：$ϵ$和$MinPts$，选择不同的参数会导致最终聚类的结果千差万别，因此DBCSAN对于输入参数过于敏感。OPTICS算法的提出就是为了帮助DBSCAN算法选择合适的参数，降低输入参数的敏感度。OPTICS主要针对输入参数$ϵ$过敏感做的改进，OPTICS和DBSCNA的输入参数一样（$ϵ$和$MinPts$），虽然OPTICS算法中也需要两个输入参数，但该算法对$ϵ$输入不敏感（一般将$ϵ$固定为无穷大），同时该算法中并不显式的生成数据聚类，只是对数据集合中的对象进行排序，得到一个有序的对象列表，通过该有序列表，可以得到一个决策图，通过决策图可以不同$ϵ$参数的数据集中检测簇集，即：先通过固定的$MinPts$和无穷大的$ϵ$得到有序列表，然后得到决策图，通过决策图可以知道当$ϵ$取特定值时（比如$ϵ=3$）数据的聚类情况。

2.相关定义

        由于OPTICS算法是DBSCAN算法的一种改进，因此有些概念是共用的，比如：$ϵ$-邻域，核心对象，密度直达，密度可达，密度相连等，下面是与OPTICS相关的定义（假设我的样本集是$X=(x_1,x_2,...,x_m)$）：

2.1 DBSCAN相关定义

• $ϵ$-邻域：对于$x_j\in X$，其$ϵ$-邻域包含样本集$X$中与$x_j$的距离不大于$ϵ$的子样本集。$ϵ$-邻域是一个集合，表示如下，这个集合的个数记为$|N_{ϵ}(x_j)|$。
  $$N_{ϵ}(x_j)=\{x_i\in X\mid distance(x_i,x_j)\le ϵ\}$$
• 核心对象：对于任一样本$x_j\in X$，如果其$ϵ$-邻域对应的$N_{ϵ}(x_j)$至少包含$MinPts$个样本，即如果 $|N_{ϵ}(x_j)|\ge MinPts$，则$x_j$是核心对象。
• 密度直达：如果$x_i$位于$x_j$的$ϵ$-邻域中，且$x_j$是核心对象，则称$x_i$由$x_j$密度直达。反之不一定成立，即此时不能说$x_j$由$x_i$密度直达, 除非且$x_i$也是核心对象，即密度直达不满足对称性
• 密度可达：对于$x_i$和$x_j$,如果存在样本样本序列$p_1,p_2,...,p_T$,满足$p1=x_i,p_T=x_j$, 且$p_{t+1}$由$p_t$密度直达，则称$x_j$由$x_i$密度可达。也就是说，密度可达满足传递性。此时序列中的传递样本 $p_1,p_2,...,p_{T-1}$均为核心对象，因为只有核心对象才能使其他样本密度直达。 密度可达也不满足对称性，这个可以由密度直达的不对称性得出。
• 密度相连：对于$x_i$和$x_j$,如果存在核心对象样本$x_k$，使**$x_i$和$x_j$均由$x_k$密度可达**，则称$x_i$和$x_j$密度相连。密度相连关系满足对称性。

2.2 OPTICS相关定义

        在上述DBSCAN定义的基础上，OPTICS在引入了两个算法需要的定义：

• 核心距离（core-distance）：样本$x\in X$，对于给定的$ϵ$和$MinPts$，使得$x$成为核心点的最小邻域半径称为$x$的核心距离，其数学表达如下，$N_{ϵ}^i(x)$代表集合$N_{ϵ}(x)$中与节点$x$第$i$近邻的节点，如$N_{ϵ}^1(x)$表示$N_{ϵ}(x)$中与$x$最近的节点

$$cd(x)=\{\begin{array}{ll}undefined& |N_{ϵ}(x)|<MinPts\\ d(x,N_{ϵ}^{MinPts}(x))& |N_{ϵ}(x)|>=MinPts\end{array}$$

• 可达距离（reachability-distance）：设$x,y\in X$,对于给定的$ϵ$和$MinPts$，$y$关于$x$的可达距离定义为：
  $$rd(y,x)=\{\begin{array}{ll}undefined& |N_{ϵ}(x)|<MinPts\\ max\{cd(x),d(x,y)\}& |N_{ϵ}(x)|>=MinPts\end{array}$$
   特别的，当$x$为核心点时（相应的参数为$ϵ$和$MinPts$），可按照下式来理解$rd(y,x)$：
  $$rd(y,x)=min\{\eta :y\in N_{\eta }(x)且|N_{\eta }(x)|\ge MinPts\}$$
   即$rd(y,x)$表示 使得“$x$成为核心点”，“$y$可以从$x$直接密度可达” 同时成立的最小邻域半径。

可达距离这里可能不太好理解，先记住一点，每一个点都有两个新属性：可达距离，核心距离

3.算法思想

        假设我们的数据集为$X=(x_1,x_2,...,x_m)$，OPTICS算法的目标是输出一个有序排列，以及每个元素的两个属性值：核心距离，可达距离。为此引入如下的数据结构：

• $p_i，i=1,2,...,N$：OPTICS算法的输出有序列表，例如$p=\{10,100,4,...\}$表示：在集合X中的数据，第10号节点首先被处理，然后第100号节点被处理，然后第4号节点被处理（即节点被处理的顺序列表）
• $c_i，i=1,2,...,N$：第$i$号节点的核心距离，例如$c=\{1.2,1.4,4.5,...\}$表示：在集合X中的数据，第1号节点的核心距离为1.2，第1号节点的核心距离为1.4，第1号节点的核心距离为4.5
• $r_i，i=1,2,...,N$：第$i$号节点的可达距离，例如$r=\{3.4,3.1.4,4.5,...\}$表示：在集合X中的数据，第1号节点的可达距离为3.4，第1号节点的可达距离为3.1，第1号节点的可达距离为4.5

3.1算法流程

输入：样本集$X=(x_1,x_2,...,x_m)$，邻域参数$(ϵ,MinPts)$

1. 初始化核心对象集合$\Omega =\varnothing$
2. 遍历$X$的元素，如果是核心对象，则将其加入到核心对象集合$\Omega$中
3. 如果核心对象集合$\Omega$中元素都已经被处理，则算法结束，否则转入步骤4.
4. 在核心对象集合$\Omega$中，随机选择一个未处理的核心对象$o$，首先将$o$标记为已处理，同时将$o$压入到有序列表$p$中，最后将$o$的$ϵ$-邻域中未访问的点，根据可达距离的大小（计算未访问的邻居点到$o$点的可达距离）依次存放到种子集合$seeds$中。
5. 如果种子集合$seeds=\varnothing$，跳转到3，否则，从种子集合$seeds$中挑选可达距离最近的种子点$seed$，首先将其标记为已访问，首先将$seed$标记为已处理，同时将$seed$压入到有序列表$p$中，然后判断$seed$是否为核心对象，如果是将$seed$中未访问的邻居点加入到种子集合中，重新计算可达距离。（计算种子集合中距离$seed$点的可达距离）跳转到5。

说明：

• 第一点，第一个被处理的对象是不存在可达距离的 （因为没有被计算过），只有进入过$seeds$的点才能计算可达距离

3.2算法伪代码

• OPTICS算法伪代码

• update算法伪代码

4.算法实现

4.1使用numpy实现OPTICS算法

import numpy as np
import matplotlib.pyplot as plt
import time
import operator
from scipy.spatial.distance import pdist
from scipy.spatial.distance import squareform
def compute_squared_EDM(X):
  return squareform(pdist(X,metric='euclidean'))
# 显示决策图
def plotReachability(data,eps):
    plt.figure()
    plt.plot(range(0,len(data)), data)
    plt.plot([0, len(data)], [eps, eps])
    plt.show()
# 显示分类的类别
def plotFeature(data,labels):
    clusterNum = len(set(labels))
    fig = plt.figure()
    scatterColors = ['black', 'blue', 'green', 'yellow', 'red', 'purple', 'orange', 'brown']
    ax = fig.add_subplot(111)
    for i in range(-1, clusterNum):
        colorSytle = scatterColors[i % len(scatterColors)]
        subCluster = data[np.where(labels == i)]
        ax.scatter(subCluster[:, 0], subCluster[:, 1], c=colorSytle, s=12)
    plt.show()
def updateSeeds(seeds,core_PointId,neighbours,core_dists,reach_dists,disMat,isProcess):
    # 获得核心点core_PointId的核心距离
    core_dist=core_dists[core_PointId]
    # 遍历core_PointId 的每一个邻居点
    for neighbour in neighbours:
        # 如果neighbour没有被处理过，计算该核心距离
        if(isProcess[neighbour]==-1):
            # 首先计算改点的针对core_PointId的可达距离
            new_reach_dist = max(core_dist, disMat[core_PointId][neighbour])
            # 如果可达距离没有被计算过，将计算的可达距离赋予
            if(np.isnan(reach_dists[neighbour])):
                reach_dists[neighbour]=new_reach_dist
                seeds[neighbour] = new_reach_dist
            # 如果可达距离已经被计算过，判读是否要进行修改
            elif(new_reach_dist<reach_dists[neighbour]):
                reach_dists[neighbour] = new_reach_dist
                seeds[neighbour] = new_reach_dist
    return seeds
def OPTICS(data,eps=np.inf,minPts=15):
    # 获得距离矩阵
    orders = []
    disMat = compute_squared_EDM(data)
    # 获得数据的行和列(一共有n条数据)
    n, m = data.shape
    # np.argsort(disMat)[:,minPts-1] 按照距离进行 行排序 找第minPts个元素的索引
    # disMat[np.arange(0,n),np.argsort(disMat)[:,minPts-1]] 计算minPts个元素的索引的距离
    temp_core_distances = disMat[np.arange(0,n),np.argsort(disMat)[:,minPts-1]]
    # 计算核心距离
    core_dists = np.where(temp_core_distances <= eps, temp_core_distances, -1)
    # 将每一个点的可达距离未定义
    reach_dists= np.full((n,), np.nan)
    # 将矩阵的中小于minPts的数赋予1，大于minPts的数赋予零，然后1代表对每一行求和,然后求核心点坐标的索引
    core_points_index = np.where(np.sum(np.where(disMat <= eps, 1, 0), axis=1) >= minPts)[0]
    # 用于标识是否被处理，没有被处理，设置为-1
    isProcess = np.full((n,), -1)
    # 遍历所有的核心点
    for pointId in core_points_index:
        # 如果核心点未被分类，将其作为的种子点，开始寻找相应簇集
        if (isProcess[pointId] == -1):
            # 将点pointId标记为当前类别(即标识为已操作)
            isProcess[pointId] = 1
            orders.append(pointId)
            # 寻找种子点的eps邻域且没有被分类的点，将其放入种子集合
            neighbours = np.where((disMat[:, pointId] <= eps) & (disMat[:, pointId] > 0) & (isProcess == -1))[0]
            seeds = dict()
            seeds=updateSeeds(seeds,pointId,neighbours,core_dists,reach_dists,disMat,isProcess)
            while len(seeds)>0:
                nextId = sorted(seeds.items(), key=operator.itemgetter(1))[0][0]
                del seeds[nextId]
                isProcess[nextId] = 1
                orders.append(nextId)
                # 寻找newPoint种子点eps邻域（包含自己）
                # 这里没有加约束isProcess == -1，是因为如果加了，本是核心点的，可能就变成了非和核心点
                queryResults = np.where(disMat[:, nextId] <= eps)[0]
                if len(queryResults) >= minPts:
                    seeds=updateSeeds(seeds,nextId,queryResults,core_dists,reach_dists,disMat,isProcess)
                # 簇集生长完毕，寻找到一个类别
    # 返回数据集中的可达列表，及其可达距离
    return orders,reach_dists
def extract_dbscan(data,orders, reach_dists, eps):
    # 获得原始数据的行和列
    n,m=data.shape
    # reach_dists[orders] 将每个点的可达距离，按照有序列表排序（即输出顺序）
    # np.where(reach_dists[orders] <= eps)[0]，找到有序列表中小于eps的点的索引，即对应有序列表的索引
    reach_distIds=np.where(reach_dists[orders] <= eps)[0]
    # 正常来说：current的值的值应该比pre的值多一个索引。如果大于一个索引就说明不是一个类别
    pre=reach_distIds[0]-1
    clusterId=0
    labels=np.full((n,),-1)
    for current in reach_distIds:
        # 正常来说：current的值的值应该比pre的值多一个索引。如果大于一个索引就说明不是一个类别
        if(current-pre!=1):
            # 类别+1
            clusterId=clusterId+1
        labels[orders[current]]=clusterId
        pre=current
    return labels
data = np.loadtxt("cluster2.csv", delimiter=",")
start = time.clock()
orders,reach_dists=OPTICS(data,np.inf,30)
end = time.clock()
print('finish all in %s' % str(end - start))
labels=extract_dbscan(data,orders,reach_dists,3)
plotReachability(reach_dists[orders],3)
plotFeature(data,labels)

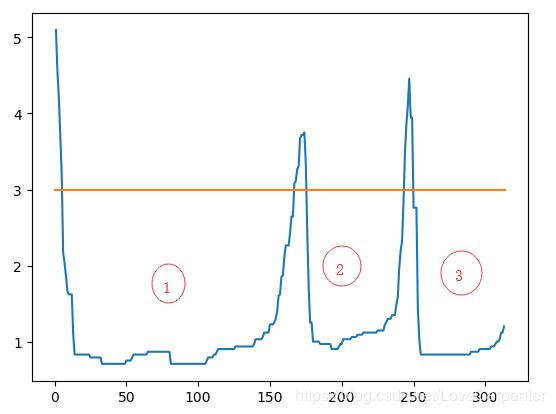
• 有序列表决策图（横坐标是处理顺序，纵坐标是该点的可达距离），举个例子，横坐标为：$[1,2,3]$，纵坐标为：$[5.5,3.6,8.4]$。说明：第一个被处理的点的可达距离为5.5，第二个被处理的点的可达距离为3.6，第三个被处理的点的可达距离为8.4。同时在该图中可以看出，当eps取3时，原数据集可以被分为3个类别（决策图有一个凹槽）.

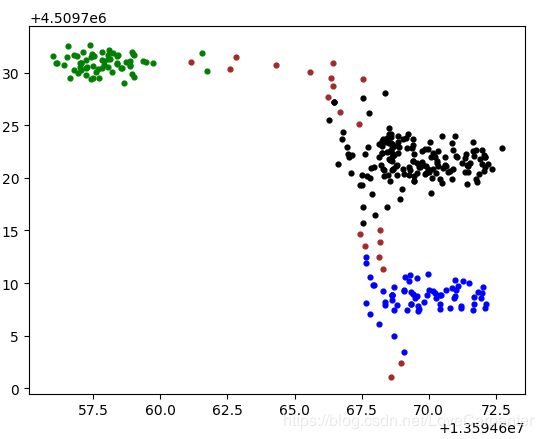
• 聚类结果可视化图（棕色是离群点）

5.数据及代码下载地址

• GitHub的数据及代码下载地址为：GitHub的数据及代码下载链接（如果从GitHub下载代码，麻烦给小Demo一个Star，您的支持是我最大的动力）