Leetcode #42. Trapping Rain Water 雨水收集 解题报告

1 解题思想

原题给定一个X轴上的取值，可以视为一个凸起的墙，高度就是对应的Y值，现在问如果下了一场雨，那么这些凸起的地方一共可以收集到多少的雨水？

那么如何才能收集呢？从图片上可以推出的就是，任意两个凸起的中间，有比两边最矮一边还要更矮的凹陷，就可以收集到雨水了。

所以做法就是，找出这些所有凹陷。
那么根据我的经验总结，从左往右找的方法如下：

1、任何一个位置i的凸起，正好能和位置j（j>i，j的高度也大于等于i的）围成一个独立的容器，注意是独立的，这时候可以单独计算这个容器的接收量，并接下来从j继续找。

2、如果j找不到是不是就没有了呢？不，因为我的1里的假设是i和不小于i高度的围成，但是i也可以和比i更矮的围起来不是么？那么这时候选择比i小的最大的一个位置k为另一个边缘，计算雨水量，然后再从k位置继续寻找

具体的做法，看我的代码注释。。

总之我的思想，就是找到每一个独立的能盛水的地方，且优先考虑左边凸起高度不大于右边的（必须这么考虑，如果只考虑2，那么计算出来的盛水量会小于实际的），这种情况是一个完整的盛水容器。如果没有，我们在考虑情况2 ，找到另一个独立的容器

2 原题

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

For example,
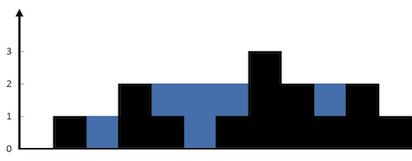
Given [0,1,0,2,1,0,1,3,2,1,2,1], return 6.

The above elevation map is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped. Thanks Marcos for contributing this image!

3 AC解

public class Solution {
    /**
     * 核心思想，要能够接住水，那么一定是两个比较高的在一起才能
     * 题目给了指示是两个指针，所以依然一个slower 一个 faster，
     * 我的目标是，独立的找到每一个单独的容器
     * 
     * slower标示左边缘，faster右边缘
     * 
     * 那么在寻找的时候首先肯定是，faster正好是第一个大于slower高度的地方，那么这时候我们就得到一个容器了
     * 
     * 那如果找不到faster，是不是就说没有容器了？
     * 不，我们在找faster时还要同时记录一个停留点，stoppoint，他是小于slower高度里最大的那一个，这个点和slower也能作为一个容器
     * 
     * 在计算完当前容器后，slower移动到faster的位置，faster重新往后进行搜索。。
     * 
     * 
     * 我没有看网上攻略，Hard的题目，不知道还有更好的解决方法么，欢迎交流
     * */
    public int trap(int[] height) {
        int total=0;
        int slower=0,faster=1;
        int n=height.length,i,tmp;
        while(faster//在结束前找到
            int stopPoint=faster,max=-1,min;
            while(fasterif(height[faster]>height[stopPoint])
                    stopPoint=faster;
                faster++;
            }
            //如果没找到，那么把那个特殊的点给faster，他也可以作为边缘
            if(faster>=height.length ){
                faster=stopPoint;
            }
            //计算当前容量
            tmp=0;
            min=Math.min(height[faster],height[slower]);
            for(i=slower+1;ireturn total;

    }
}