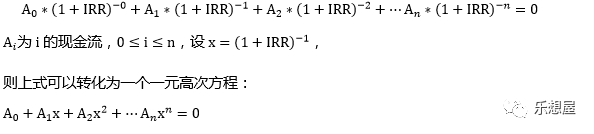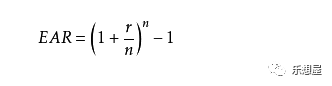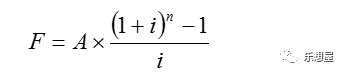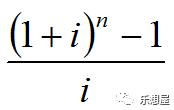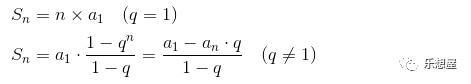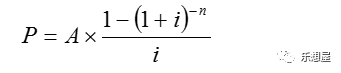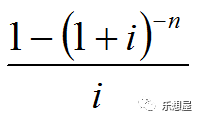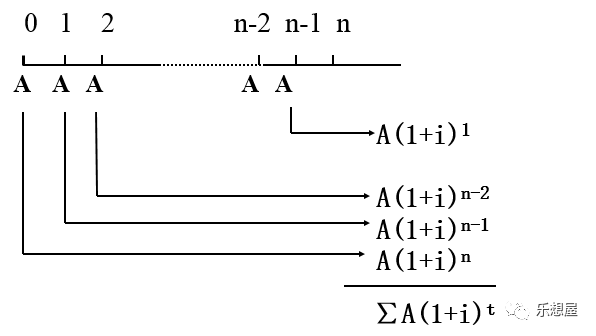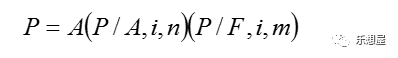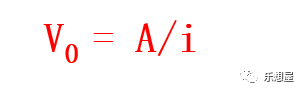年金、净现值NPV、IRR、现值PV、终值FV、EAR等常见概念
1、各种基本概念:
资金是有时间价值的,比如我们卖出去一笔货,总是希望尽快提前收到货款,今年的钱仅仅因为通货膨胀,也会比明年同等金额的钱更值钱。
1)资金的时间价值是指资金在周转过程中由于时间因素形成的差额值,表现为投资收益减去风险报酬和通货膨胀贴水后的那部分价值。
2)现金流:是指企业在一定会计期间按照现金收付实现制,通过一定经济活动产生的现金流入、现金流出及其总量情况的总称,即企业一定时期的现金和现金等价物的流入和流出的数量。通俗点说,将现金的流出和流入记成流水账,正负相抵就是净现金流。
3)折现:将未来收益或支出折算成当前价值称为折现。
4)折现率(discount):是根据资金具有的时间价值这一特性,按照复利计息原理,把未来一定时期的预期收益折合成现值的一种比率。资金的时间价值到底有多大,评价标准就是折现率。折现率可以用来计算现金流的净现值。
5)折现(Discounted Cash):把未来某时点的现金流量折算为起始时点值的过程。
6)复利:指计算资金的终值时,不仅计算本金的利息,而且还要将经过一定时期本金获得的利息也加入本金计算利息,逐期滚算,利上加利。
7)净现值NPV(Net Present Value)指的是一个项目预期实现的现金流入的现值与实施该项计划的现金支出的现值的差额。净现值为正值的项目可以为股东创造价值,净现值为负值的项目会损害股东价值。
净现值=未来报酬的总现值-初始投资现值。
净现值案例:
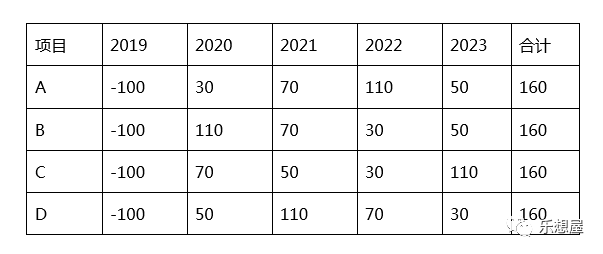
2018年假设有4个备选投资项目,都是2019年投入现金100万,2020年-2023年为项目的生命期,每年都有净现金流流入,总额都是160万收益。
项目现金流预测如下(单位:万)
到底应该选择哪一个方案?
假定公司确定的折现率为10%,我们先通过折现率,将每个项目2019年~2023年的收益都折算成今年(2018年)的资金现值。
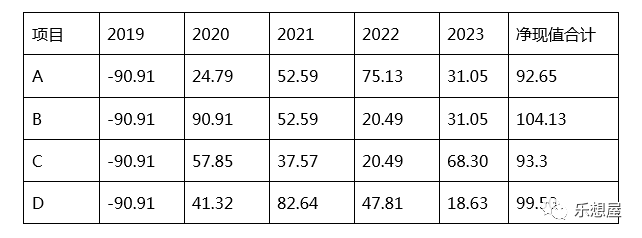
依次计算其他项目,项目折算成2018年净现值的收益(折现率:10%):
可以看出B方案最好,我们投资100万,所有收益都折算成今天的货币价值,净收益相当于104.13万元。或者对比的说法,如果银行的存款年利率是10%,我们这100万没有选择存款,但是选择投资B项目,就比银行多赚了104.13万元。
假设银行的存款利息很高,比如高达45.84%,我们那这个利率作为折现率,算下到底是银行存款好,还是项目好,算法一样,只是将10%的折现率修改成45.84%。结果如下:
项目折算成2018年净现值的收益(折现率:45.84%):
项目 |
2019 |
2020 |
2021 |
2022 |
2023 |
净现值合计 |
A |
-68.57 |
14.11 |
22.57 |
24.32 |
7.58 |
0 |
B |
-68.57 |
51.72 |
22.57 |
6.63 |
7.58 |
19.93 |
C |
-68.57 |
32.91 |
16.12 |
6.63 |
16.67 |
3.77 |
D |
-68.57 |
23.51 |
35.46 |
15.47 |
4.55 |
10.43 |
如果做A项目,相当于100万存银行,年化收益率45.84%。如果做B项目,同样的折现率,则可比A方案多赚19.93万。
实际上,这个45.84%就是A项目的内部收益率IRR。
8)IRR(Internal Return Rate):资金流入现值总额与资金流出现值总额相等,也即净现值等于零时的折现率。内部 收益率是效率型指标,它反映项目所占用资金的 盈利率,是考察项目资金使用效率的重要指标。一般情况下,内部收益率大于等于基准收益率时,该项目是可行的。
比如上述项目A,如果碰巧找到一个折现率(如45.84%),而这个折现率去折算我们未来的投资收益时,可以使净现值总和为0,那么这个折现率就是我们说的内部收益率。
IRR既然是资金流入和流出现值的总额,就可以用公式如下表示:
求解x时可以用插值法,也可以采用其他方法,如果每年的资金流金额相等,可以转化为年金计算问题。在此不做推导,Excel有公式直接计算IRR。
公式:IRR(values, [guess])
参数说明:
Values,数组或单元格的引用,这些单元格包含用来计算内部收益率的数字,Values 必须包含至少一个正值和一个负值,以计算返回的内部收益率。IRR 使用值的顺序来说明现金流的顺序。 一定要按您需要的顺序输入支出值和收益值。如果数组或引用包含文本、逻辑值或空白单元格,这些数值将被忽略。
Guess,对函数 IRR 计算结果的估计值,可有可无。
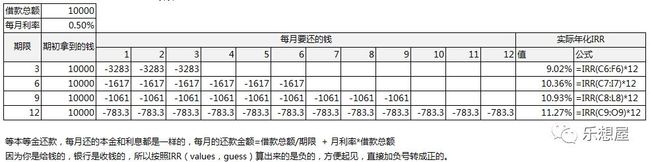
之前做了一个IRR和月利率的转化表,分享出去的时候,经常被产品或者其他的风控同事询问,IRR你这个表是怎么计算。如果你不想整太多高复杂的东西,就一期一期把你的现金流填上去,直接就能计算出IRR。
案例:经常贷款或分期的同学,你一定需要这个。借款1万元,每月等本等金(每月相等的本金、相同的利息)还给银行,月利率0.5%,算算看你的实际年化IRR,是不是月利率*期限?
所以假设你借了12个月的钱,你以为你的利率是0.5%*12=6%,实际上,算上资金的时间价值,你给给银行的利率是11.27%。最划算的贷款还是等额本金和等额本息,月利率*12就是实际的年化IRR。
9)有效年利率EAR(Effective interest)和名义利率(Norminal interest)。
在企业筹资和借贷活动中,经常会遇到这样的情况,给定年利率,但计息周期是半年、季、或月,也即按照半年、季、月复利。
有效年利率EAR(Efficient Annual Rate)指在按照给定的计息期利率和每年复利次数计算利息时,能够产生相同结果的每年复利一次的年利率。
其中,r为名义利率,n为一年内的计息次数。
比如年名义利率10%,计息周期分别是年、半年、季、月、日的年实际利率
上述的EAP,如果n趋向于无穷大时,
可知,当年名义利率r相等的情况下,计息次数越多,则EAR越高,但EAR是有一个极限的,当计息周期n无穷大时:
10)现值(Present Value):发生在(或折算为)某一现金流量序列起点的现金流价值。简称P。
11)终值(Future Value):发生在(或折算为)某一现金流量序列终点的现金流量价值,简称F。
以下以年金为案例讲述终值和现值以及资金的时间价值。
2、年金
年金是(Annuity)指等额、定期的系列收支。
-
等期等额付款赊购
等期等额偿还贷款
等期等额发放养老金
等期等额支付工程款
每年相同的销售收入等,都属于年金收付形式。
按年金收付时点,可以将年金划分为普通年金、预付年金、递延年金、永续年金。
2-1普通年金(Ordinary Annuity)
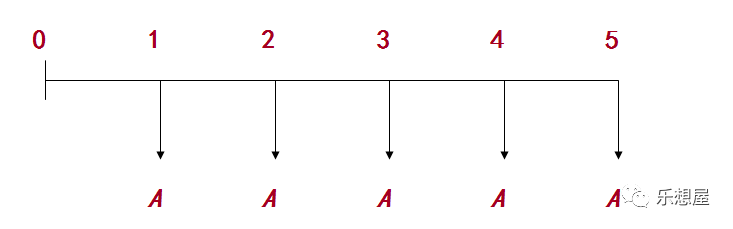
普通年金是指各期期末收付的年金。其收付形式为:
1)普通年金终值的计算示意图
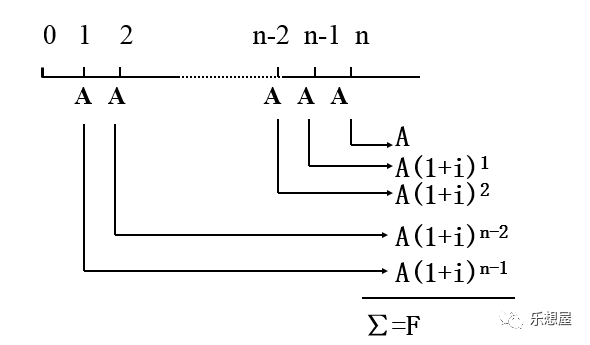
普通年金终值是一定时期内每期期末等额收付款项的复利终值之和。
这是一个等比数列,公比q=(1+i),可以运用等比数列求和公式,也可在等式两端同时乘以(1+i),然后再把所得的式子与原来的式子相减,即可求得:
其中,
是普通年金为1元、利率为i、经过n期的年金终值。记作(F/A,i,n)年金终止系数,可以通过查阅“年金终值系数表”取得相关系数。
附:等比数列公式
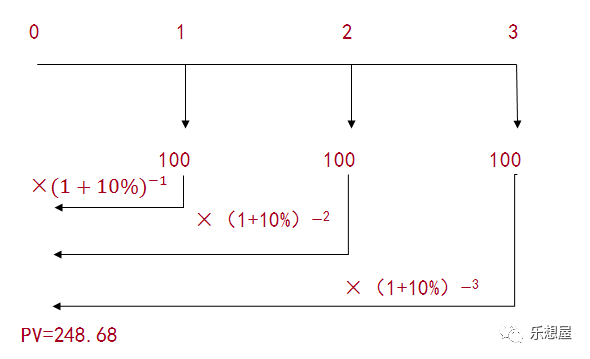
案例:假设你每年年末存入银行100元,连续存3年,在银行存款利率为10%的情况下,则在第3年末你将积累多少钱?
2)普通年金的现值推导公式
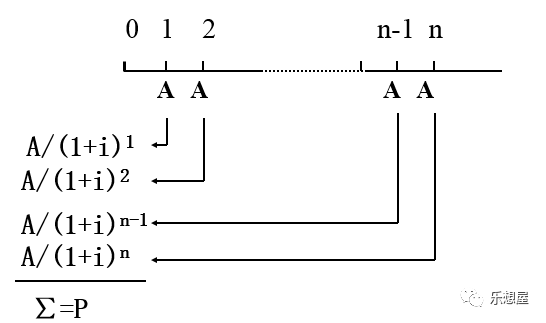
普通年金现值,是指一定期间内每期期末等额的系列收付款项的现值之和。
年金的现值是等于一系列年金的复利现值之和。
现值公式:
推导得到:
其中
是普通年金为1元、利率为i、经过n期的年金现值,记作(P/A,i,n)。
它可以通过查阅“年金现值系数表”取得相关系数。
案例:假设你需要在每年年末取出100元,连续取3年,在银行存款利率为10%的情况下,你现在要向银行存入多少钱?
2-2 预付年金
指在每期的期初有等额收付款项的年金。
预付年金和普通年金的现金流次数相同,只是由于发生时间不同,终值和现值的计算有所差异。就终值计算来看,预付年金比普通年金多计算一期利息;而就现值计算来看,预付年金又恰好比普通年金少贴现一期利息。
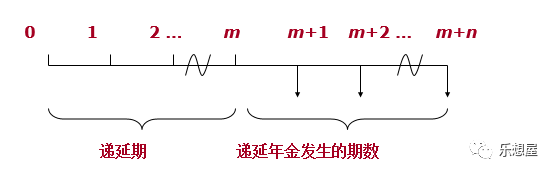
2-3 递延年金(Deferred Annuity)
递延年金(Deferred Annuity)是指第一次年金收付形式发生在第二期或第二期以后的年金。支付形式如下图
横轴表示时间的延续,数字表示各期的顺序号,A表示各期收付款的金额,m表示递延期数,n表示首付款次数。
1)递延年金终值计算:
由于递延期m与终值无关,只需考虑递延年金发生期数n。
案例:假设江南公司拟一次性投资开发某农庄,预计该农庄能存续15年,但是前5年不会产生净收益,从第6年开始,每年的年末产生净收益5万元。在考虑资金时间价值的因素下,若农庄的投资报酬率为10%,该农庄给企业带来累计收益为多少?
根据终值公式:
F =50000×(F/A,10%,10)
=50000×15.937
=796850(元)
2)递延年金的现值计算:
递延年金的现值与递延期数相关,递延的期数越长,其现值越低。
可以有三种计算方法:
方法1:把递延期以后的年金套用普通年金公式折现到m期的现值,然后再向前折现至第一期初。
方法2:把递延期每期期末都当作有等额的年金收付A,把递延期和以后各期看成是一个普通年金,计算出这个普通年金的现值。再把递延期虚增的年金现值减掉即可。
方法3:先求递延年金终值,再折现为现值。
案例:假设江南公司拟一次性投资开发某农庄,预计该农庄能存续15年,但是前5年不会产生净收益,从第6年开始,每年的年末产生净收益5万元。假设江南公司决定投资开发该农庄,根据其收益情况,该农庄的累计投资限额为多少?
用方法2计算出的结果如下:
P=50000×(P/A,10%,15)-50000×(P/A,10%,5)
=50000×7.6061-50000×3.7908
=190765.00(元)
2-4 永续年金
永续年金是无限期等额收付的特种年金,没有终值,只有现值。永续年金可视为普通年金的特殊形式,即期限趋于无穷的普通年金。
现值的计算公式为:
其中,A表示每年的年金,i为利率
2-5 Excel中常用的财务函数解释
计算的函数
| 公式 | 解释 | 详情 |
| FV | 终值 | FV(Rate,Nper,Pmt,Pv,Type) |
| PV | 现值 | PV(Rate,Nper,Pmt,Fv,Type) |
| PMT | 每期的资金 | PMT(Rate,Nper,Pv,Fv,Type) |
| NPER | 期限 | NPER(Rate,Pmt,Pv,Fv,Type) |
| RATE | 年化收益率 | RATE(Nper,Pmt,Pv,Fv,Type) |
涉及的参数:
| 参数英文 | 含义 |
| rate | 收益率(每一期的复利率) |
| nper | total number of periods 指收付年金的次数 |
| pmt | payment每期年金,如果输入为0,表示计算的不是年金问题 |
| pv | 开始的现金流入量 |
| fv | 结束的现金流入量 |
| type | 取值0或1:0指现金流发生在期末,1指现金流发生在期初 |