数据可视化三:Matlab数据可视化(二)
数据可视化三:Matlab数据可视化(二)
目录:
1、三维曲线绘制:
2、统计图绘制:
3、动画绘制:
1、三维曲线绘制:
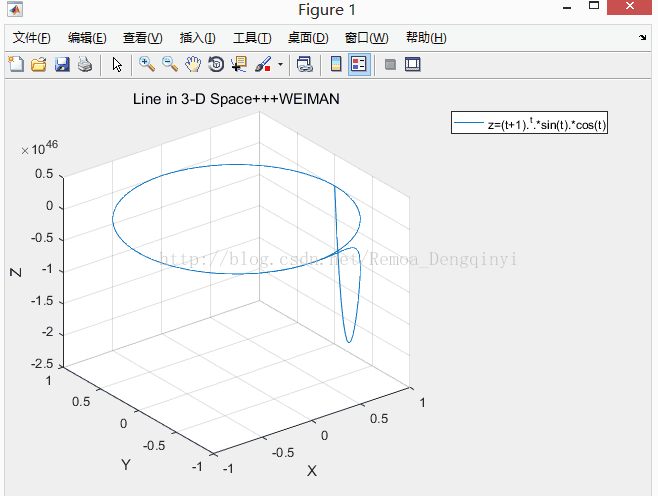
1.1 设计函数y=sin(t), x=cos(t), z=(t+1).^t.*sin(t).*cos(t),并使用plot3函数绘制这三个函数的曲线。
t=0:pi/100:10*pi;
y=sin(t);
x=cos(t);
z=(t+1).^t.*sin(t).*cos(t);
plot3(x,y,z);
title('Line in 3-D Space+++WEIMAN');
xlabel('X');ylabel('Y');zlabel('Z');
grid on;
思考:plot3函数的用法?
答:plot3可以画出三维空间中的曲线。plot3(x1,y1,z1) 其中x1,y1,z1为相同维数的向量,分别存储各个点坐标。
程序分析:
t=0:pi/100:10*pi; % 定义t列向量,这个向量的第一个元素是0,最后一个元素是10π,而每两个元素之间的差是π/100;
y=sin(t); % 定义y函数
x=cos(t); % 定义x函数
z=(t+1).^t.*sin(t).*cos(t); % 定义z函数
plot3(x,y,z); % 绘制三维曲线
title('Line in 3-D Space+++WEIMAN'); % 定义图形标题
xlabel('X');ylabel('Y');zlabel('Z'); % X轴注解,Y轴注解,Z轴注解
grid on; % 绘制网格线
legend( 'z=(t+1).^t.*sin(t).*cos(t)'); % 添加标签
运行结果:
图1.1 运行结果
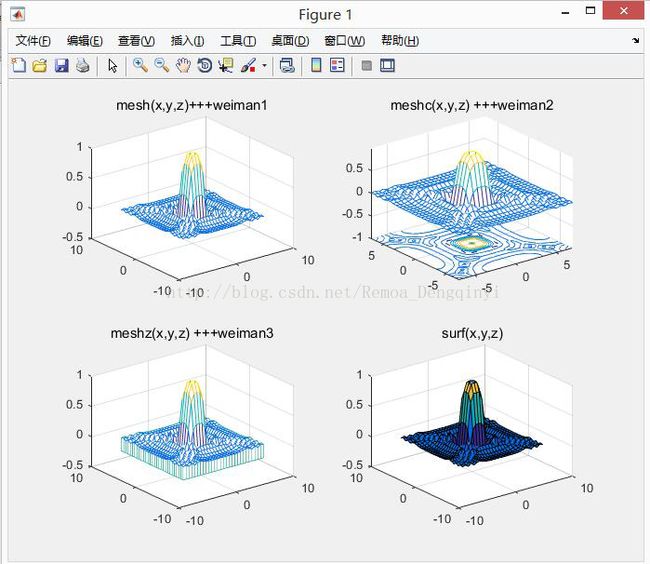
1.2 设计函数z=sin(x+sin(y))-x/10;,分别绘制带等高线的三维网格曲面函数meshc和带底座的三维网格曲面函数meshz。并使用函数surf绘制该函数图像
[x,y]=meshgrid(-7:0.5:7);
z=sin(sqrt(x.^4+y.^4))./sqrt(x.^4+y.^4+eps);
subplot(2,2,1);
mesh(x,y,z);
title('mesh(x,y,z)+++weiman1')
subplot(2,2,2);
meshc(x,y,z);
title('meshc(x,y,z) +++weiman2')
subplot(2,2,3);
meshz(x,y,z)
title('meshz(x,y,z) +++weiman3')
subplot(2,2,4);
surf(x,y,z);
title('surf(x,y,z)');
思考:meshc,meshz,surf函数的用法?
答:(1)meshgrid:将xoy平面用定义的x、y向量网格化,之后对其中的每一个得到的点求其对应的函数值,最后用mesh将函数图像做出来。
(2)mesh:用于绘制立体网状图
(3)meshz:为曲面加上围裙
(4)meshc:同时画出网状图与等高线
(5)surf:绘制立体曲面图
(6)程序分析:
close all % 关闭所有的图形视窗;
[x,y]=meshgrid(-7:0.5:7); % 将x,y向量网格化,从-7到7的正方形区间内,各点间隔0.5,即x轴有29个点,y轴有29个点,所以,绘制的三维图像网格中,共有29*29=841个点;
z=sin(sqrt(x.^4+y.^4))./sqrt(x.^4+y.^4+eps); % 定义z函数;
subplot(2,2,1); % 同时画出2*2=4个小图形于一个视窗之中,这是定义的第一个区域;
mesh(x,y,z); % 在第一个区域画出x,y,z函数的图像;
title('mesh(x,y,z)+++weiman1') %给第一个区域的图形定义标题;
subplot(2,2,2); % 定义的第二个区域;
meshc(x,y,z); % 在第二个区域画出x,y,z函数的图像并同时画出等高线;
title('meshc(x,y,z) +++weiman2') % 给第二个区域的图形定义标题;
subplot(2,2,3); % 定义的第三个区域;
meshz(x,y,z) % 在第三个区域画出x,y,z函数的图像并带底座(围裙);
title('meshz(x,y,z) +++weiman3') % 给第三个区域的图形定义标题;
subplot(2,2,4); % 定义的第四个区域;
surf(x,y,z); % 在第四个区域绘制x,y,z函数的立体曲面图;
title('surf(x,y,z)'); % 给第四个区域的图形定义标题;
运行结果:
图1.2 运行结果
1.3 三维图形编辑(精细控制)实验:设计实验演示验证用view、rotate、colordef、colormap、shading、light、lighting、material、surfl等函数对三维图形进行精细控制的方法。
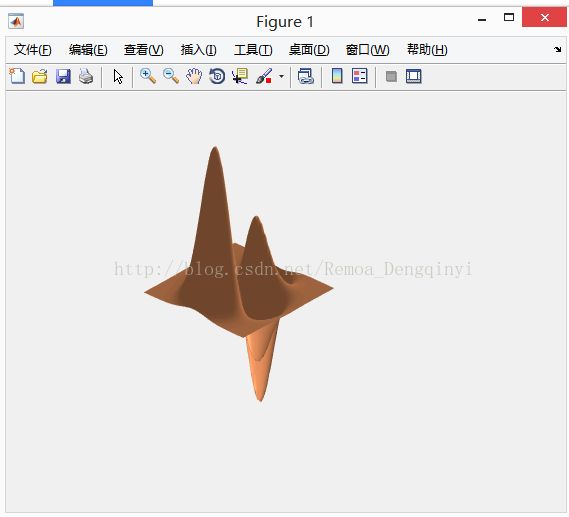
函数surfl功能
z=peaks(20);
>> colordef white ;
>> colormap jet;
>> shading interp;
>> surfl(z)
title(' surfl +++weiman')
函数rotate功能
z=peaks(20);
subplot(1,2,1);surf(z);title('Default+++weiman'); subplot(1,2,2);h=surf(z);title('Rotated+++weiman'); rotate(h,[-2,-2,0],20,[2,2,0]);
函数view功能
z=peaks(10);
>> subplot(1,2,1);surf(z);title('Default+++weiman ');
>> subplot(1,2,2);
>> subplot(1,2,2);h=surf(z);title('view+++weiman ');
>> view(0,40);
答:(1)view:设置视点的函数。view(az,el):
az是azimuth(方位角)的缩写,el是elevation(仰角)的缩写。它们均以度为单位。系统缺省的视点定义为方位角-37.5°,仰角30°。
当x轴平行观察者身体,y轴垂直于观察者身体时,az=0; 以此点为起点,绕着z轴顺时针运动,az为正,逆时针为负。
el 为观察者眼睛与xy平面形成的角度。
当观察者的眼睛在xy平面上时,el=0; 向上el为正,向下为负;
AZ = -37.5, EL = 30 是默认的三维视角.
AZ = 0, EL = 90 是二维视角,从图形正上方向下看,显示的是xy平面.
AZ = EL = 0 看到的是xz平面.
AZ = 180,EL=0 是从背面看到的xz平面.
VIEW(2) 设置默认的二维视角, AZ = 0, EL = 90.
VIEW(3) 设置默认的三维视角, AZ = -37.5, EL = 30.
(2)rotate:旋转,h表示画图函数的句柄,用于后续操作
(3)colordef:背景颜色设定
(4)colormap:用map矩阵映射当前的色图,可用于控制曲面图的颜色,比如:autumn spring summer winter jet(默认) bone colorcube cool flag 等等
图1.3 colormap色图
(5)shading:阴影函数控制曲面和图形对象的颜色着色,用来处理色彩效果。shading 是用来处理色彩效果的,分以下三种:
no shading 一般的默认模式 即shading faceted
shading flat 在faceted的基础上去掉图上的网格线
shading interp 在flat的基础上进行色彩的插值处理,使色彩平滑过渡
(6)light:设置灯光。light('Color',选项一,'Style',选项二,'Position',选项三):选项一表示光的颜色,取RGB三元组或相应的颜色字符。选项二可取为'infinite'和'local'两个值,分别表示无穷远光和近光。选项三去三维坐标点组成的向量形式[x,y,z]。对远光,它表示光穿过该点射向原点;对于近光,它表示光源所在位置。假如函数不包含任何参数,则采用缺省设置:白光、无穷远光、穿过(1,0,1)射向坐标原点。
(7)lighting:设置照明模式
(8)material:设置材质
(9)surfl:绘制的三维曲面有光照效果
源码分析:
①函数surfl功能
z=peaks(20); % 定义z为peaks函数,peaks函数是二元高斯分布的概率密度函数, z = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) ...
- 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) ...
- 1/3*exp(-(x+1).^2 - y.^2)
peaks(n)函数,n越大,相邻点间隔越小,图形越平滑,返回的z是一个二维矩阵。执行peaks(20)函数,结果如图:
图1.4 运行结果
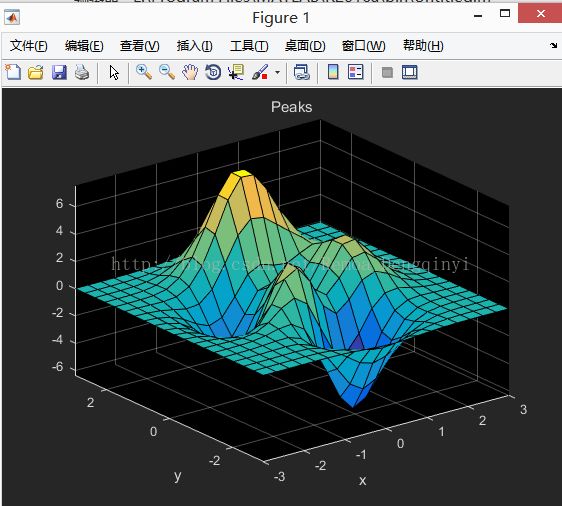
colordef black; % 定义背景颜色为黑色,效果如图:
图1.5 运行结果
colormap jet; % 设置曲面颜色为默认的jet色图,效果如图:
图1.6 运行结果
shading interp; % 去掉网格并使色彩平滑过渡,效果如图:
图1.7 运行结果
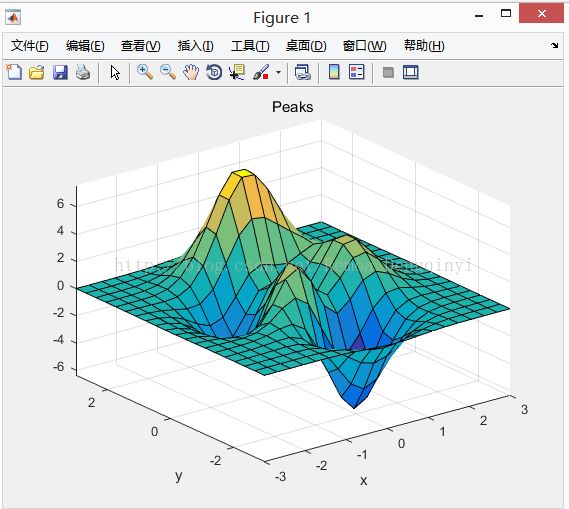
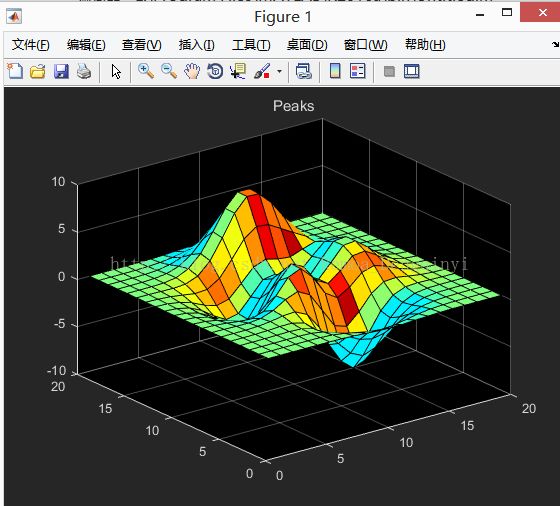
surfl(z) % 设置带有光照效果
图1.8 运行结果
title('Peaks') % 设置标题
②函数rotate功能
z=peaks(20); % 定义z为peaks函数
subplot(1,2,1); % 定义两个区域,此处为第一个区域
surf(z); % 在第一个区域里绘制z所指对象
title('Default+++weiman'); % 设置标题
subplot(1,2,2); % 此处为第二个区域
h=surf(z); % 定义h为z的三维着色表面
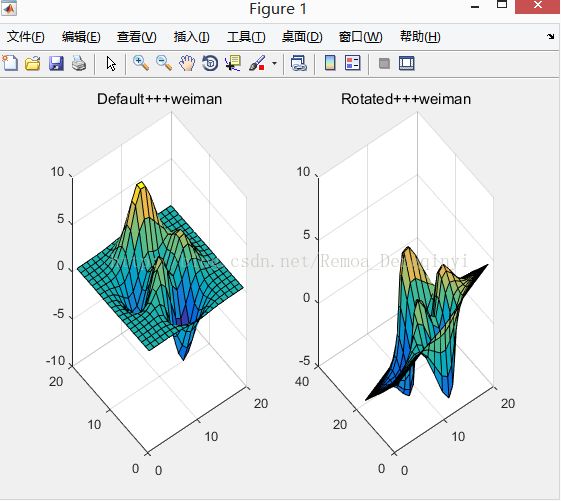
title('Rotated+++weiman'); % 设置标题
rotate(h,[-2,-2,0],20,[2,2,0]); % 在第二个区域绘制h所指对象,旋转轴的列向量为-2,-2,0,旋转角度为20度,旋转轴的起点坐标为(2,2,0),默认为原点
运行结果:
图1.9 运行结果
函数view功能
z=peaks(10); % 定义z为peaks函数
subplot(1,2,1); % 定义一行两列两个区域,此处为第一个区域
surf(z); % 绘制z所指对象的三维着色表面图
title('Default+++weiman '); % 定义标题
subplot(1,2,2);% 第二个区域
h=surf(z); % 绘制h所指对象的三维着色表面图
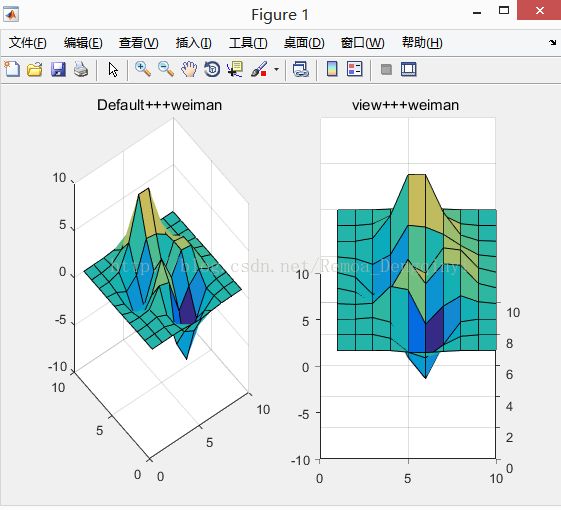
title('view+++weiman ');% 定义标题
view(0,40); % 设置视点
运行结果如图:
图1.10 运行结果
2、统计图绘制:
2.1 设计实验演示验证面域图(area)
x=-2:2
Y=[3,8,9,4,1;6,3,5,2,7;5,4,3,8,6] %(3*5)的Y数组
CS=flipud(cumsum(Y))
area(x',Y',0)
legend('因素A','因素B','因素C')
grid on,
colormap('jet')
title('area+++weiman')
思考:自己提供数据,画出面域图?
答:(1)程序分析
x=-2:2 % 定义x从-2到2
Y=[3,8,9,4,1;6,3,5,2,7;5,4,3,8,6] % (3*5)的Y数组
CS=flipud(cumsum(Y)) % cumsum计算一个数组各行的累加值,cumsum(Y)的结果为:
3 8 9 4 1
9 11 14 6 8
14 15 17 14 14
flipud实现矩阵的上下翻转,flipud(cumsum(Y))结果为:
14 15 17 14 14
9 11 14 6 8
3 8 9 4 1
area(x',Y',0) % area是填充画图区域的命令,如果Y是矩阵,把Y按列作为填充区域
legend('因素A','因素B','因素C') % 插入标签
grid on, % 添加网格
colormap('jet') % 设置色图为jet
title('area+++weiman') % 添加标题
运行结果:
图2.1 运行结果
2.2 设计实验演示验证直方图(bar、barh、bar3、bar3h)
x=-2:2;
Y=[3,7,2,5,1;3,7,5,2,1;5,4,1,2,5];
subplot(2,2,1)
bar(x',Y','stacked')
title('bar +++weiman')
xlabel('x'),ylabel('\Sigma y'), colormap('jet')
legend('因素A','因素B','因素C')
subplot(2,2,2)
bar3h(x',Y','grouped')
title(' bar3h +++weiman')
subplot(2,2,4)
bar3(x',Y','stacked')
title('bar3 +++weiman')
subplot(2,2,3)
barh(x',Y', 'grouped')
title('barh +++weiman')
答:(1)bar:二维竖直直方图
(2)barh:二维水平直方图
(3)bar3:三维竖直直方图
(4)bar3h:三维水平直方图
(5)grouped:使同一组直方条紧紧靠在一起
(6)stacked:把同一组数据描述在一个直方条上
程序分析:
x=-2:2;
Y=[3,7,2,5,1;3,7,5,2,1;5,4,1,2,5];
subplot(2,2,1) % 定义2行2列四块区域,此处为第一块区域
bar(x',Y','stacked') % 在第一块区域绘制二维竖直直方图,共五组数据,同一组数据描述在一个直方条上
title('bar +++weiman')
xlabel('x')
ylabel('\Sigma y')
colormap('jet')
legend('因素A','因素B','因素C')
subplot(2,2,2)
bar3h(x',Y','grouped') % 在第二块区域绘制三维水平直方图,共五组数据,每一组中的三列数据紧紧靠在一起
title(' bar3h +++weiman')
subplot(2,2,4)
bar3(x',Y','stacked') % 在第四块区域绘制三维竖直直方图,共五组数据,同一组数据描述在一个直方条上
title('bar3 +++weiman')
subplot(2,2,3)
barh(x',Y', 'grouped') % 在第三块区域绘制二维水平直方图,共五组数据,每一组中的三列数据紧紧靠在一起
title('barh +++weiman')
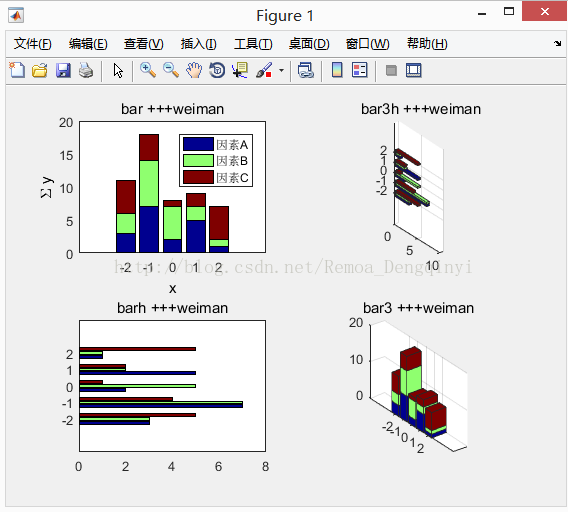
运行结果:
图2.2 运行结果
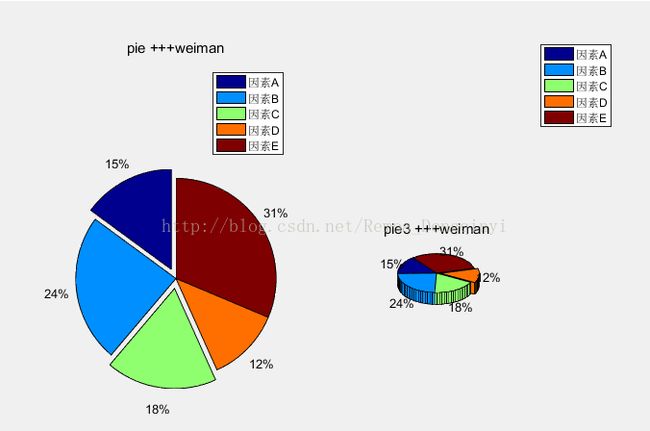
2.3 饼图(pie、pie3)
a=[1,1.6,1.2,0.8,2.1];
subplot(1,2,1)
pie(a,[1 0 1 0 0])
axis equal
title('pie +++weiman')
legend('因素A','因素B','因素C','因素D','因素E')
subplot(1,2,2)
pie3(a,double(a==min(a)))
colormap(jet)
title('pie3 +++weiman')
legend('因素A','因素B','因素C','因素D','因素E')
答:(1)pie:二维饼图
(2)pie3:三维饼图
程序分析:
a=[1,1.6,1.2,0.8,2.1];
subplot(1,2,1)
pie(a,[1 0 1 0 0]) % 列向量a为五个数值所占总数值和的百分比描绘二维饼图,其中[1 0 1 0 0]中的1表示突出显示
axis equal % axis equal将横轴纵轴的定标系数设成相同值
title('pie +++weiman')
legend('因素A','因素B','因素C','因素D','因素E')
subplot(1,2,2)
pie3(a,double(a==min(a))) % 绘制三维饼图,a中最小值的修改为double双精度数值类型,并突出显示
colormap(jet) % 设置jet色图
title('pie3 +++weiman')
legend('因素A','因素B','因素C','因素D','因素E')
运行结果:
图2.3 运行结果
2.4 散点图(scatter、scatter3、plotmatrix)
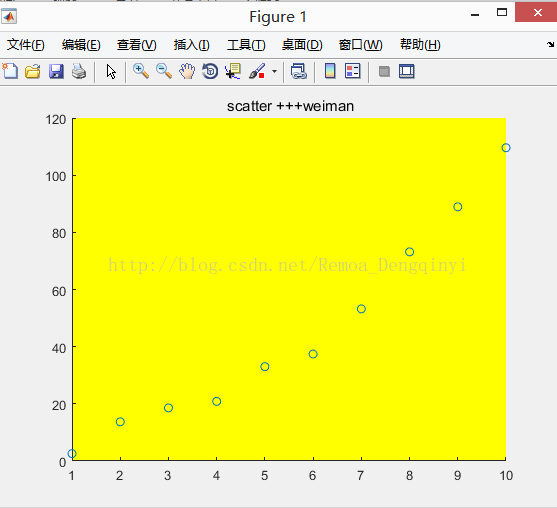
2.4.1 scatter(X,Y)
X = [1:10];
Y = X.^2 + 2 * rand(size(X));
scatter(X, Y)
set(gca,'color','y');
title(' scatter +++weiman')
答:(1)scatter:二维散点图
(2)程序分析:
X = [1:10]; % X变量的取值为1到10
Y = X.^2 + 2 * rand(size(X)); % 定义Y变量,rand是产生一个0到1的随机数,size(X)是矩阵X的大小,rand(size(X))是生成一个与X矩阵大小一样的(10行1列)矩阵,里面的元素都是随机生成的0-1的数
scatter(X, Y) % 绘制X、Y的二维散点图
set(gca,'color','y'); % 设置坐标轴范围内的背景颜色为黄色
title(' scatter +++weiman') % 设置标题
运行结果:
图2.5 运行结果
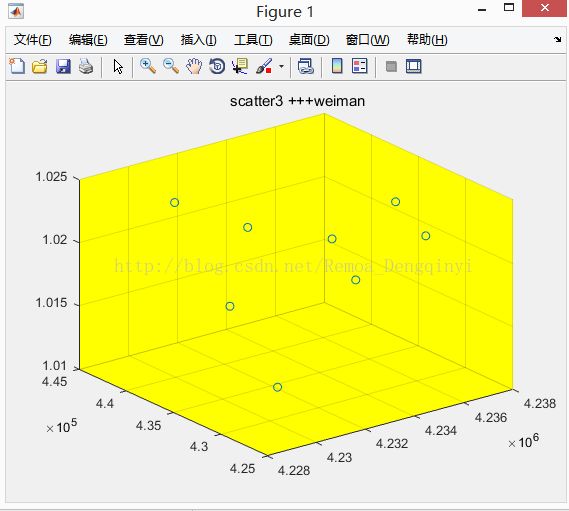
2.4.2 函数scatter3
x=[4229042.63 4230585.02 4231384.96 4231773.63 4233028.58 4233296.71 4235869.68 4236288.29];
y=[431695.4 441585.8 432745.6 436933.7 428734.4 431946.3 428705.0 432999.5];
z=[1.019 1.023 1.011 1.022 1.020 1.022 1.022 1.023];
scatter3(x,y,z)
set(gca,'color','y');
title(' scatter3 +++weiman')
注:x,y,z必须是等长度的数对(即三个等长的矢量)
答:(1)scatter3:三维散点图
(2)程序分析:
与二维散点图示例程序分析基本相同,其中xyz对应位置的值所组成对应的的坐标,故不冗述。
运行结果:
图2.6 运行结果
2.4.3 Plotmatrix函数
x=randn(100,2)
plotmatrix(x)
答:(1)plotmatrix:矩阵色块图,绘出X(p*M)与Y(p*N)的列组成的散度图(N,M)
(2)程序分析:
x=randn(100,2) % 返回一个100 * 2的随机项矩阵,其中randn是产生均值为0,方差σ^2 = 1,标准差σ = 1的正态分布的随机数或矩阵的函数。
plotmatrix(x)
运行结果:
图2.7 运行结果
3、动画绘制:
设计实验演示验证getframe与movie相结合绘制动画的方法。
%影片生成例子: 旋转一个三维表面绘图
[X, Y, Z]=peaks(50); %创建山峰图形数据
surfl(X, Y, Z) %绘制带光照的表面
axis([-10 10 -10 10 -10 10]) %限制绘图范围
axis vis3d off %三维坐标修正,关闭坐标轴箭头
axis equal %等比例显示三维坐标
shading interp %加个影子美化
colormap(copper) %着色为铜色
for i=1:360 %旋转山峰,从1到360度,每一度捕捉一帧
view(-37.5+i,30) %从水平-37.5+i度,垂直30度的方向看山 m(i)=getframe; %每从一个角度看到一张图像(帧),就存储到m
end %每次看完,水平转动1度,直到1周360度;
cla %为播放影片清除坐标
movie(m) %把刚才存到m里的图像连续播放一遍,就是影片了.
答:(1)getframe:生成每个帧
(2)movie:按照指定的速度和次数运行此动画,movie(m,n)可以播放由矩阵m所定义的画面n次,默认n时只播放一次。
运行结果如下:
图3.1 运行结果