机器学习二：最小二乘学习法

最小二乘学习法

〇、目录

主要包含了线性模型的最小二乘法理论推导，和python程序验证。

一、原理推导

回归问题（Regression）中

最小二乘学习法（Least Square）是对模型的输出 fθ(x⃗ i) f θ ( x → i ) 和训练集输出 {yi}ni=1 { y i } i = 1 n 的平方误差

JLS(θ)=12∑i=1n(fθ(x⃗ i)−yi)2 J L S ( θ ) = 1 2 ∑ i = 1 n ( f θ ( x → i ) − y i ) 2

为最小时的参数 θ θ 进行学习的方法。

∥fθ(x⃗ i)−yi∥2(2)=((fθ(x⃗ i)−yi)T(fθ(x⃗ i)−yi)−−−−−−−−−−−−−−−−−−−−−√)2=(fθ(x⃗ i)−yi)T(fθ(x⃗ i)−yi)=∑i=1n(fθ(x⃗ i)−yi)2 ‖ f θ ( x → i ) − y i ‖ ( 2 ) 2 = ( ( f θ ( x → i ) − y i ) T ( f θ ( x → i ) − y i ) ) 2 = ( f θ ( x → i ) − y i ) T ( f θ ( x → i ) − y i ) = ∑ i = 1 n ( f θ ( x → i ) − y i ) 2

因此也叫 l2 l 2 损失最小化学习。

在求解最小值时，使用求微分令其为 0 0 的 θ θ 值，因此在平方误差公式凑了一个 12 1 2 ，将微分得到的 2 2 约去。

针对线性模型 fθ(x⃗ )=θ⃗ Tϕ(x⃗ ) f θ ( x → ) = θ → T ϕ ( x → ) ，先给出结果：

∇θJLS=(∂JLS∂θ1,∂JLS∂θ2,⋯,∂JLS∂θb)T=ΦTΦθ⃗ −ΦTy⃗  ∇ θ J L S = ( ∂ J L S ∂ θ 1 , ∂ J L S ∂ θ 2 , ⋯ , ∂ J L S ∂ θ b ) T = Φ T Φ θ → − Φ T y →

推导过程：

JLS(θ⃗ )=12∥Φθ⃗ −y⃗ ∥2 J L S ( θ → ) = 1 2 ‖ Φ θ → − y → ‖ 2

=12∥⎛⎝⎜⎜ϕ1(x⃗ 1)⋮ϕ1(x⃗ n)⋯⋱⋯ϕb(x⃗ 1)⋮ϕb(x⃗ n)⎞⎠⎟⎟⎛⎝⎜⎜θ1⋮θb⎞⎠⎟⎟−⎛⎝⎜⎜y1⋮yn⎞⎠⎟⎟∥2 = 1 2 ‖ ( ϕ 1 ( x → 1 ) ⋯ ϕ b ( x → 1 ) ⋮ ⋱ ⋮ ϕ 1 ( x → n ) ⋯ ϕ b ( x → n ) ) ( θ 1 ⋮ θ b ) − ( y 1 ⋮ y n ) ‖ 2

=12∥⎛⎝⎜⎜θ1ϕ1(x⃗ 1)+⋯+θbϕb(x⃗ 1)−y1⋮θ1ϕ1(x⃗ n)+⋯+θbϕb(x⃗ n)−yn⎞⎠⎟⎟∥2 = 1 2 ‖ ( θ 1 ϕ 1 ( x → 1 ) + ⋯ + θ b ϕ b ( x → 1 ) − y 1 ⋮ θ 1 ϕ 1 ( x → n ) + ⋯ + θ b ϕ b ( x → n ) − y n ) ‖ 2

根据 l2 l 2 -Norm可得：

=12(⎛⎝⎜⎜θ1ϕ1(x⃗ 1)+⋯+θbϕb(x⃗ 1)−y1⋮θ1ϕ1(x⃗ n)+⋯+θbϕb(x⃗ n)−yn⎞⎠⎟⎟T⎛⎝⎜⎜θ1ϕ1(x⃗ 1)+⋯+θbϕb(x⃗ 1)−y1⋮θ1ϕ1(x⃗ n)+⋯+θbϕb(x⃗ n)−yn⎞⎠⎟⎟−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−⎷)2 = 1 2 ( ( θ 1 ϕ 1 ( x → 1 ) + ⋯ + θ b ϕ b ( x → 1 ) − y 1 ⋮ θ 1 ϕ 1 ( x → n ) + ⋯ + θ b ϕ b ( x → n ) − y n ) T ( θ 1 ϕ 1 ( x → 1 ) + ⋯ + θ b ϕ b ( x → 1 ) − y 1 ⋮ θ 1 ϕ 1 ( x → n ) + ⋯ + θ b ϕ b ( x → n ) − y n ) ) 2

=12⎛⎝⎜⎜θ1ϕ1(x⃗ 1)+⋯+θbϕb(x⃗ 1)−y1⋮θ1ϕ1(x⃗ n)+⋯+θbϕb(x⃗ n)−yn⎞⎠⎟⎟T⎛⎝⎜⎜θ1ϕ1(x⃗ 1)+⋯+θbϕb(x⃗ 1)−y1⋮θ1ϕ1(x⃗ n)+⋯+θbϕb(x⃗ n)−yn⎞⎠⎟⎟ = 1 2 ( θ 1 ϕ 1 ( x → 1 ) + ⋯ + θ b ϕ b ( x → 1 ) − y 1 ⋮ θ 1 ϕ 1 ( x → n ) + ⋯ + θ b ϕ b ( x → n ) − y n ) T ( θ 1 ϕ 1 ( x → 1 ) + ⋯ + θ b ϕ b ( x → 1 ) − y 1 ⋮ θ 1 ϕ 1 ( x → n ) + ⋯ + θ b ϕ b ( x → n ) − y n )

=12[(θ1ϕ1(x⃗ 1)+⋯+θbϕb(x⃗ 1)−y1)2+⋯+(θ1ϕ1(x⃗ n)+⋯+θbϕb(x⃗ n)−yn)2] = 1 2 [ ( θ 1 ϕ 1 ( x → 1 ) + ⋯ + θ b ϕ b ( x → 1 ) − y 1 ) 2 + ⋯ + ( θ 1 ϕ 1 ( x → n ) + ⋯ + θ b ϕ b ( x → n ) − y n ) 2 ]

因此，

∇θJLS=12⎛⎝⎜⎜⎜⎜⎜⎜⎜2(θ1ϕ1(x⃗ 1)+⋯+θbϕb(x⃗ 1)−y1)ϕ1(x⃗ 1)+⋯+2(θ1ϕ1(x⃗ n)+⋯+θbϕb(x⃗ n)−yn)ϕ1(x⃗ n)⋮2(θ1ϕ1(x⃗ 1)+⋯+θbϕb(x⃗ 1)−y1)ϕb(x⃗ 1)+⋯+2(θ1ϕ1(x⃗ n)+⋯+θbϕb(x⃗ n)−yn)ϕb(x⃗ n))⎞⎠⎟⎟⎟⎟⎟⎟⎟ ∇ θ J L S = 1 2 ( 2 ( θ 1 ϕ 1 ( x → 1 ) + ⋯ + θ b ϕ b ( x → 1 ) − y 1 ) ϕ 1 ( x → 1 ) + ⋯ + 2 ( θ 1 ϕ 1 ( x → n ) + ⋯ + θ b ϕ b ( x → n ) − y n ) ϕ 1 ( x → n ) ⋮ 2 ( θ 1 ϕ 1 ( x → 1 ) + ⋯ + θ b ϕ b ( x → 1 ) − y 1 ) ϕ b ( x → 1 ) + ⋯ + 2 ( θ 1 ϕ 1 ( x → n ) + ⋯ + θ b ϕ b ( x → n ) − y n ) ϕ b ( x → n ) ) )

利用矩阵乘法，可将求导得到的 ϕ1(x⃗ 1) ϕ 1 ( x → 1 ) 等提出来：

∇θJLS=⎛⎝⎜⎜ϕ1(x⃗ 1)⋮ϕb(x⃗ 1)⋯⋱⋯⋯ϕ1(x⃗ n)⋮⋯ϕb(x⃗ n)⎞⎠⎟⎟⋅(Φθ⃗ −y⃗ )=ΦTΦθ⃗ −ΦTy⃗  ∇ θ J L S = ( ϕ 1 ( x → 1 ) ⋯ ⋯ ϕ 1 ( x → n ) ⋮ ⋱ ⋮ ϕ b ( x → 1 ) ⋯ ⋯ ϕ b ( x → n ) ) ⋅ ( Φ θ → − y → ) = Φ T Φ θ → − Φ T y →

即得。

通过求解 ΦTΦθ⃗ −ΦTy⃗ =0 Φ T Φ θ → − Φ T y → = 0 即可得到通过最小二乘法学习的参数 θ⃗  θ → ，但在大多数情况下，由于数据量远远大于参数数量，因此 Φ Φ 是一个奇异矩阵，并非方阵，我们不能通过简单的通过他的逆矩阵求出解，因此这里需要引入一个伪逆矩阵的新概念，用来解决此问题。

二、实践

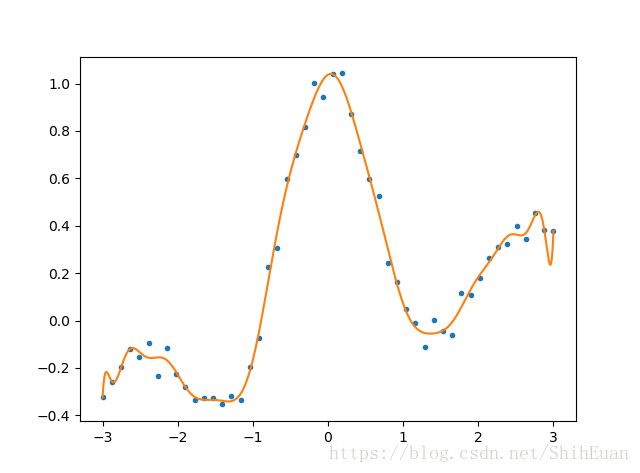
学习了最小二乘法的原理之后，通过python程序来巩固一下。
本程序根据上面对线性模型的推导，基函数使用三角多项式形式，即：

ϕ(x)=(1,sinx2,cosx2,sin2x2,cos2x2,⋯,sin15x2,cos15x2)T ϕ ( x ) = ( 1 , sin ⁡ x 2 , cos ⁡ x 2 , sin ⁡ 2 x 2 , cos ⁡ 2 x 2 , ⋯ , sin ⁡ 15 x 2 , cos ⁡ 15 x 2 ) T

而数据我们使用近似的 sinc(x)=sin(πx)πx s i n c ( x ) = sin ⁡ ( π x ) π x 函数加上随机误差来生成得到。

程序如下：

    #!/usr/bin/env python3
    # -*- coding: utf-8 -*-

    __author__ = 'shiheuan'

    import numpy as np
    import matplotlib.pyplot as plt


    def LeastSquares():
        N = 1000
        n = 50 # len(x)
        x = np.array([np.linspace(-3.,3.,n)])
        # print(x)

        X = np.array([np.linspace(-3.,3.,N)])
        # 图像形态 + 随机误差
        y = np.sin(np.pi*x)/(np.pi*x)+0.1*x+0.05*np.random.randn(1,n)

        P = np.ones([31,N])
        p = np.ones([31,n])

        for i in range(15):
            P[2*i+1,:] = np.sin((i+1)/2*X)
            P[2*i+2,:] = np.cos((i+1)/2*X)
            p[2*i+1,:] = np.sin((i+1)/2*x)
            p[2*i+2,:] = np.cos((i+1)/2*x)

        print(p)
        p = p.T
        print(p)
        P = P.T
        pp = np.linalg.pinv(p)
        pp = np.dot(p.T, p)
        # print(pp)
        # pinv 与 inv 的区别
        ppi = np.linalg.pinv(pp)
        # print(ppi)
        pp_ = np.dot(ppi, p.T)
        # print(pp_)
        t = np.dot(pp_, y.T)
        # print(t)
        # print(y)
        F = np.dot(P, t).T

        plt.plot(x[0,:],y[0,:],'.')
        plt.plot(X[0,:],F[0,:])
        plt.show()

    LeastSquares()

执行结果：