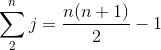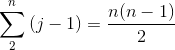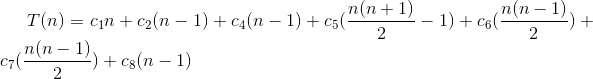2.2 分析算法

分析算法的结果意味着预测算法需要的资源。通过分析求解某个问题的几种候选算法，我们可以选出一种最有效的算法。这种分析可能指出不止一个可行的候选算法，但是在这个过程中，我们往往可以抛弃几个较差的算法。

插入排序算法的分析

过程INSERTION-SORT需要的时间依赖于输入：排序1000个数比排序三个数需要更长的时间。依据它们已被排序的程度，INSERTION-SORT可能需要不同数量的时间来排序两个具有相同规模的输入序列。

• 输入规模：对许多问题，如排序或计算离散傅里叶变换，最自然的量度是输入中的项数，例如，待排序数组的规模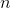。对于其他许多问题，如两个整数相乘，输入规模的最佳量度是用通常的二进制记号表示输入所需的总位数。有时，用两个数而不是一个数来描述输入规模可能更合适。对于研究的每个问题，我们将指出所使用的输入规模量度。
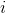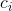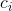• 运行时间：一个算法在特定输入上的运行时间是指执行的基本操作数或步数。执行每行伪代码需要常量时间。虽然一行与另一行可能需要不同数量的时间，但是我们假定第行的每次执行需要时间，其中是一个常量。这个观点与RAM模型是一致的，并且也反映了伪代码在大多数真实计算机上如何实现。

我们首先给出过程INSERTION-SORT中，每条语句的执行时间和执行次数。对，其中，假设表示对那个值第5行执行while循环测试的次数。当一个for或while循环按通常的方式退出时，执行测试的次数比执行循环体的次数多1.我们假定注释是不可执行的语句，所以他们不需要时间。

INSERTION-SORT(A)	代价	次数
for  = 2 to
		- 1
//Insert into the sorted sequence .	0	- 1
		- 1
while  > 0 and  >
		- 1

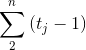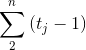该算法的运行时间是执行每条语句的运行时间之和。需要执行步且执行次的一条语句将贡献給总运行时间。为计算在具有个值的输入上INSERTION-SORT的运行时间，我们将代价与次数列对应元素之积求和，得：

即使对给定规模的输入，一个算法的运行时间也可能依赖于给定的是该规模下的哪个输入。例如，在INSERTION-SORT中，若输入数组已排好序，则出现最佳情况。这时，对每个 = 2, 3, ... , ，我们发现在第5行，当取其初值时，有 ≤ 。从而对 = 2, 3, ... , ，有 = 1，该最佳情况的运行时间为：

把该运行时间表示为，其中常量和依赖于语句代价。因此它是的线性函数。

若输入数组已反向排序，即按递减序排好序，则导致最坏情况。我们必须将每个元素与整个已排序子数组中的每个元素进行比较，所以对 = 2, 3, ... , ，有 = 。

和

最坏的情况下，INSERTION-SORT的运行时间为

我们可以把该最坏情况运行时间表示为，其中常量、、又依赖于。因此，它是的二次函数。

在分析插入排序时，我们既研究了最佳情况，其中输入数组已排好序，又研究了最坏情况，其中输入数组已反向排好序。然而，我们往往集中于只求最坏情况运行时间，即对规模为的任何输入，算法的最长运行时间。下面给出这样做的三点理由：

• 一个算法的最坏运行情况运行时间给出了任何输入的运行时间的一个上界。知道了这个界，就能确保该算法绝不需要更长的时间。我们不必对运行时间做出某种复杂的猜测并可以期望它不会变得更坏。
• 对某些算法，最坏情况经常出现。例如，当在数据库中检索一条特定信息时，若该信息不在数据库中出现，则检索算法的最坏情况会经常出现。在某些应用中，对缺失信息的检索可能是频繁的。
• “平均情况”往往与最坏情况大致一样差。假定随机选择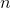个数并应用插入排序。需要多长时间来确定在子数组的什么位置插入元素？平均来说，中的一半元素小于，一半元素大于。所以，平均来说，我们检查子数组的一半，那么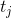大约为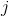/2。导致的平均情况运行时间结果像最坏情况运行时间一样，也是输入规模的一个二次函数。

在某些特定情况下，我们会对一个算法的平均情况运行时间感兴趣；贯穿于本书，我们将看到概率分析技术被用于各种算法。平均情况分析的范围有限，因为对于特定的问题，什么构成一种“平均”输入并不明显。我们常常假定给定规模的所有输入具有相同的可能性。实际上，该假定可能不成立，但是，有时可以使用随机化算法，它做出一些随机的选择，以允许进行概率分析并产生某个期望的运行时间。

现在我们做出一种更简化的抽象：即我们真正感兴趣的运行时间的增长率或增长量级。所以我们只考虑公式中最重要的项（例如，），因为当的值很大时，低阶项相对来说不太重要。我们也忽略最重要的项的常系数，因为对大的输入，在确定计算效率时常量因子不如增长率重要。对于插入排序，当我们忽略低阶项和最重要的项的常系数时，只剩下最重要的项中的因子。我们记插入排序具有最坏情况运行时间 （读作“theta n平方”）。

如果一个算法的最坏情况运行时间具有比另一个算法更低的增长量级，那么我们通常认为前者比后者更有效。由于常量因子和低阶项，对于小的输入，运行时间具有较高增长量级的一个算法与运行时间具有较低增长量级的另一个算法相比，其可能需要较少的时间。但是对足够大的输入，例如，一个的算法在最坏情况下比另一个的算法要运行得更快。

2.2-1 用 记号表示函数。

2.2-2 考虑排序存储在数组中的个数：首先找出中的最小元素并将其与[1]中的元素进行交换。接着，找出中的次最小元素并将其与[2]中的元素进行交换。对中前-1个元素按该方式继续。该算法称为选择算法，写出其伪代码。该算法维持的循环不变式是什么？为什么它只需要对前-1个元素，而不是对所有个元素运行？用记号给出选择排序的最好情况与最坏情况运行时间。

  for i = 1 to A.length - 1
      min = i
      for j = i + 1 to A.length
          if A[j] < A[min]
              min = j
      temp = A[i]
      A[i] = A[min]
      A[min] = temp

In the best-case time (the array is sorted), the body of the if is never invoked. The number of operations (counting the comparison as one operation) is:

In the worst-case time (the array is reversed), the body of the if is invoked on every occasion, which doubles the number of steps in the inner loop, that is:

Both are clearly .

2.2-3 再次考虑线性查找问题（参见练习2.1-3）。假定要查找的元素等可能地为数组中的任意元素，平均需要检查输入序列的多少元素？最坏情况又如何呢？用记号给出线性查找平均情况和最坏情况运行时间。证明你的答案。

最好1次；最坏次；平均次

2.2-4 应如何修改任何一个算法，才能使之具有良好的最好情况运行时间？

We can modify it to handle the best-case efficiently. For example, if we modify merge-sort to check if the array is sorted and just return it, the best-case running time will be .