数据结构--图--拓扑排序/关键路径/AOE/AOV

1.基本概念：

AOV网：用顶点表示活动，用弧表示活动间的优先关系的有向图称为顶点表示活动的网络（Activity On Vertex Network）,简称AOV-网。
AOE网：在一个表示工程的带权有向图中，用顶点表示事件，用有向边表示活动，用边上的权值表示活动的持续时间，这种有向图的边表示活动的网，我们称之为AOE网（Activity On Edge Network）
{路径长度：路径上各个活动所持续的时间之和
关键路径：从源点到汇点具有最大长度的路径
关键活动：在关键路径上的活动}
拓扑排序：对一个有向图构造拓扑序列的过程。
关键路径：由于在AOE网中有些活动可以并行地进行，所以完成工程的最短时间是从开始点到完成点的最长路径的长度（这里所说的路径长度是指路径上各活动持续时间之和，不是路径上弧的数目）。路径长度最长的路径叫做关键路径。

2.算法实现思路

拓扑排序

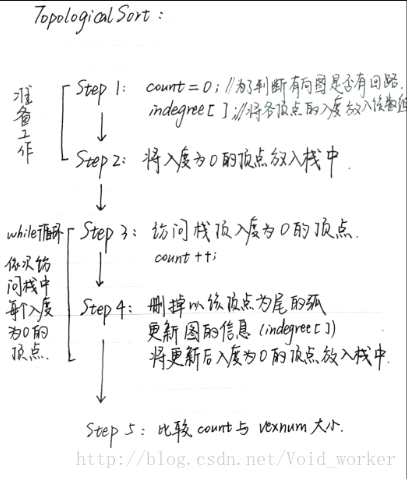
从AOV网中选择一个入度为0的顶点输出，然后删去此顶点，并删除以此顶点为尾的弧，继续重复此步骤，直到输出全部顶点或者AOV网中不存在入读为0的顶点为止。
（拓扑排序的过程中，需要删除顶点，显然用邻接表会更加方便。考虑到算法过程中始终要查找入度为0的顶点，因此我们设置一个indegree数组，用来存放各顶点的入度数目。）

关键路径

拓扑排序主要是为解决一个工程能否顺序进行的问题，但有时我们还需要解决工程完成需要的最短时间问题。我们如果要对一个流程图获得最短时间，就必须要分析它们的拓扑关系，并且找到当中最关键的流程。这个流程的时间就是最短时间。
一个活动的最早开始时间= 最晚开始时间，则该活动是关键活动，活动间的路径是关键路径。

3.拓扑排序/关键路径 实现代码

拓扑排序

#include
#include

#define OK 1
#define ERROR 0
#define OVERFLOW -2
#define TRUE 1
#define FALSE 0
#define STACK_INIT_SIZE 10
#define STACKINCREMENT 2
#define MAX_VERTEX_SIZE 20
#define INFINITY INT_MAX

typedef int Status;
typedef int InfoType;
typedef int VertexType;
typedef int VRType;
typedef enum {DG,DN,UDG,UDN} GraphKind;
typedef int SElemType;

typedef struct 
{
    SElemType *base,*top;
    int stacksize;
}SqStack;


typedef struct ArcNode
{
    VRType adjvex;
    int weight;
    struct ArcNode *next;
}ArcNode;

typedef struct VNode
{
    VertexType data;
    ArcNode *firstarc;
}VNode,AdjList[MAX_VERTEX_SIZE];

typedef struct 
{
    int vexnum,arcnum;
    AdjList vertices;
    GraphKind kind;
}ALGraph;

Status InitStack(SqStack *S);
Status DestroyStack(SqStack *S);
Status Push(SqStack *S, SElemType e);
Status Pop(SqStack *S, SElemType *e);
Status StackEmpty(SqStack S);

Status CreateGraph(ALGraph *G){

    ArcNode *p,*q;
    VNode v1,v2;
    int i,j,sign1,sign2;


    (*G).kind = DG;
    printf("有向图\n");
    printf("请输入顶点数，弧的数\n");
    scanf("%d%d",&(*G).vexnum,&(*G).arcnum);
    printf("请初始化顶点\n");
    for(i = 0; i < (*G).vexnum; ++i){
        scanf("%d",&(*G).vertices[i].data);
        (*G).vertices[i].firstarc = NULL;
    }

    printf("请初始化弧\n");
    printf("输入格式：顶点1 顶点2 （表示顶点1邻接到顶点2）\n\n");
    for(i = 0; i < (*G).arcnum; ++i){
        sign1 = -1;
        sign2 = -1;
        scanf("%d%d",&v1.data,&v2.data);
        for(j = 0; j < (*G).vexnum; ++j){
            if(v1.data == (*G).vertices[j].data)
                sign1 = j;
            if(v2.data == (*G).vertices[j].data)
                sign2 = j;
        }

        p = (ArcNode*)malloc(sizeof(ArcNode));
        if(!p)
            exit(OVERFLOW);
        p->next = NULL;
        p->adjvex = sign2;

        q = (*G).vertices[sign1].firstarc;
        if(!q)
            (*G).vertices[sign1].firstarc = p;
        else{
            while(q->next != NULL)
                q = q->next;
            q->next = p;
        }
    }
    return OK;
}

Status Find(ALGraph G,int *indegree){ //查找函数，将图G各顶点的入度保存到indegree数组中
    int i;
    ArcNode *p;
    for(i = 0; i < G.vexnum; ++i)
        indegree[i] = 0;
    for(i = 0; i < G.vexnum; ++i){
        for(p = G.vertices[i].firstarc; p != NULL; p = p->next){
            indegree[p->adjvex]++;
        }
    }
    for(i = 0; i < G.vexnum; ++i)
        printf("indegree [%d] = %d \n",i,indegree[i]);
    return OK;
}

Status TopologicalSort(ALGraph G){  //拓扑排序

    int i,x,k,count = 0;
    SqStack S;
    int indegree[G.vexnum];
    ArcNode *p;

    InitStack(&S);
    Find(G,indegree);
    for(i = 0; i < G.vexnum; ++i){
        if(indegree[i] == 0){
            Push(&S,i);
        }
    }
    while(!StackEmpty(S)){
        Pop(&S,&x);
        printf("%d ", x);
        count++;
        for(p = G.vertices[x].firstarc; p != NULL; p = p->next){
            k = p->adjvex;
            if(--indegree[k] == 0){
                Push(&S,k);
            }
        }

    }
    DestroyStack(&S);
    if(count > G.vexnum){
        return ERROR;
    }
    return OK;

}



int main(){

    ALGraph G;
    CreateGraph(&G);
    TopologicalSort(G);
    return 0;
}

Status InitStack(SqStack *S){
    (*S).base = (SElemType *)malloc(sizeof(SElemType));
    if(!(*S).base)
        exit(OVERFLOW);
    (*S).top = (*S).base;
    (*S).stacksize = STACK_INIT_SIZE;
    return OK;
}

Status DestroyStack(SqStack *S){
    free((*S).base);
    (*S).base = (*S).top = NULL;
    (*S).stacksize = 0;
    return OK;
}

Status Push(SqStack *S, SElemType e){

    if((*S).top - (*S).base >= (*S).stacksize){
        (*S).base = (SElemType *)realloc((*S).base,(STACKINCREMENT + S->stacksize) * sizeof(SElemType));
        if(!S->base)
            exit(OVERFLOW);
        (*S).top = S->base + S->stacksize;
        S->stacksize += STACKINCREMENT;
    }
    *((*S).top++) = e;
  //  (*S).top ++;
    return OK;
}


Status Pop(SqStack *S, SElemType *e){
    if(S->top == S->base){
        printf("栈空\n");
        return ERROR;
    }
    *e = *--S->top;
    return OK;
}

Status StackEmpty(SqStack S){
    if(S.base == S.top)
        return TRUE;
    else
        return FALSE;
}

关键路径

#include
#include

#define OK 1
#define ERROR 0
#define OVERFLOW -2
#define TRUE 1
#define FALSE 0
#define STACK_INIT_SIZE 10
#define STACKINCREMENT 2
#define MAX_VERTEX_SIZE 20
#define INFINITY INT_MAX

typedef int Status;
typedef int InfoType;
typedef int VertexType;
typedef int VRType;
typedef enum {DG,DN,UDG,UDN} GraphKind;
typedef int SElemType;

typedef struct 
{
    SElemType *base,*top;
    int stacksize;
}SqStack;


typedef struct ArcNode
{
    VRType adjvex;
    int weight;
    struct ArcNode *next;
}ArcNode;

typedef struct VNode
{
    VertexType data;
    ArcNode *firstarc;
}VNode,AdjList[MAX_VERTEX_SIZE];

typedef struct 
{
    int vexnum,arcnum;
    AdjList vertices;
    GraphKind kind;
}ALGraph;

int etv[MAX_VERTEX_SIZE];
int ltv[MAX_VERTEX_SIZE];

Status InitStack(SqStack *S);
Status DestroyStack(SqStack *S);
Status Push(SqStack *S, SElemType e);
Status Pop(SqStack *S, SElemType *e);
Status StackEmpty(SqStack S);

Status CreateGraph(ALGraph *G){

    ArcNode *p,*q;
    VNode v1,v2;
    int i,j,sign1,sign2;
    int value;


    (*G).kind = DG;
    printf("有向图\n");
    printf("请输入顶点数，弧的数\n");
    scanf("%d%d",&(*G).vexnum,&(*G).arcnum);
    printf("请初始化顶点\n");
    for(i = 0; i < (*G).vexnum; ++i){
        scanf("%d",&(*G).vertices[i].data);
        (*G).vertices[i].firstarc = NULL;
    }

    printf("请初始化弧\n");
    printf("输入格式：顶点1 顶点2 权值（表示顶点1邻接到顶点2）\n\n");
    for(i = 0; i < (*G).arcnum; ++i){
        sign1 = -1;
        sign2 = -1;
        scanf("%d%d%d",&v1.data,&v2.data,&value);
        for(j = 0; j < (*G).vexnum; ++j){
            if(v1.data == (*G).vertices[j].data)
                sign1 = j;
            if(v2.data == (*G).vertices[j].data)
                sign2 = j;
        }

        p = (ArcNode*)malloc(sizeof(ArcNode));
        if(!p)
            exit(OVERFLOW);
        p->next = NULL;
        p->weight = value;
        p->adjvex = sign2;

        q = (*G).vertices[sign1].firstarc;
        if(!q)
            (*G).vertices[sign1].firstarc = p;
        else{
            while(q->next != NULL)
                q = q->next;
            q->next = p;
        }
    }
    return OK;
}

Status Find(ALGraph G,int *indegree){ //查找函数，将图G各顶点的入度保存到indegree数组中
    int i;
    ArcNode *p;
    for(i = 0; i < G.vexnum; ++i)
        indegree[i] = 0;
    for(i = 0; i < G.vexnum; ++i){
        for(p = G.vertices[i].firstarc; p != NULL; p = p->next){
            indegree[p->adjvex]++;
        }
    }
    for(i = 0; i < G.vexnum; ++i)
        printf("indegree [%d] = %d \n",i,indegree[i]);
    return OK;
}

Status TopologicalSort(ALGraph G, SqStack *T){  //拓扑排序

    int i,x,k,count = 0;
    SqStack S;
    int indegree[G.vexnum];
    ArcNode *p;

    InitStack(&S);
    InitStack(T);
    Find(G,indegree);
    for(i = 0; i < G.vexnum; ++i)
        etv[i] = 0;
    for(i = 0; i < G.vexnum; ++i){
        if(indegree[i] == 0){
            Push(&S,i);
        }
    }
    while(!StackEmpty(S)){
        Pop(&S,&x);
        Push(T,x);
        count++;
        for(p = G.vertices[x].firstarc; p != NULL; p = p->next){
            k = p->adjvex;
            if(--indegree[k] == 0){
                Push(&S,k);
            }
            if(etv[k] < etv[x] + p->weight)
                etv[k] = etv[x] + p->weight;
        }
    }
    DestroyStack(&S);
    if(count > G.vexnum){
        return ERROR;
    }
    printf("\n");
    return OK;

}

Status CriticalPath(ALGraph G){

    int i,k,x;
    int ete,lte;
    ArcNode *p;
    SqStack T;

    InitStack(&T);
    TopologicalSort(G,&T);
    for(i = 0; i < G.vexnum; ++i){
        ltv[i] = etv[G.vexnum - 1];
    }

    while(!StackEmpty(T)){
        Pop(&T,&x);
        for(p = G.vertices[x].firstarc; p != NULL; p = p->next){
            k = p->adjvex;
            if(ltv[x] > ltv[k] - p->weight)
                ltv[x] = ltv[k] - p->weight;
        }
    }

    for(i = 0; i < G.vexnum; ++i){
        for(p = G.vertices[i].firstarc; p != NULL; p = p->next){
            k = p->adjvex;
            ete = etv[i];
            lte = ltv[k] - p->weight;
            if(ete == lte){
                printf("Criticalpath: <%d,%d> length: %d\n",i,k,p->weight);
            }
        }
    }
    DestroyStack(&T);
    return OK;
}


int main(){

    ALGraph G;
    CreateGraph(&G);
    CriticalPath(G);
    return 0;
}

 Status InitStack(SqStack *S)
 { /* 构造一个空栈S */
   (*S).base=(SElemType *)malloc(STACK_INIT_SIZE*sizeof(SElemType));
   if(!(*S).base)
     exit(OVERFLOW); /* 存储分配失败 */
   (*S).top=(*S).base;
   (*S).stacksize=STACK_INIT_SIZE;
   return OK;
 }



 Status DestroyStack(SqStack *S)
 { /* 销毁栈S，S不再存在 */
   free((*S).base);
   (*S).base=NULL;
   (*S).top=NULL;
   (*S).stacksize=0;
   return OK;
 }

 Status ClearStack(SqStack *S)
 { /* 把S置为空栈 */
   (*S).top=(*S).base;
   return OK;
 }

Status Push(SqStack *S,SElemType e)
 { /* 插入元素e为新的栈顶元素 */
   if((*S).top-(*S).base>=(*S).stacksize) /* 栈满，追加存储空间 */
   {
     (*S).base=(SElemType *)realloc((*S).base,((*S).stacksize+STACKINCREMENT)*sizeof(SElemType));
     if(!(*S).base)
       exit(OVERFLOW); /* 存储分配失败 */
     (*S).top=(*S).base+(*S).stacksize;
     (*S).stacksize+=STACKINCREMENT;
   }
   *((*S).top)++=e;
   return OK;
 }

 Status Pop(SqStack *S,SElemType *e)
 { /* 若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK；否则返回ERROR */
   if((*S).top==(*S).base)
     return ERROR;
   *e=*--(*S).top;
   return OK;
 }

 Status StackEmpty(SqStack S)
 { /* 若栈S为空栈，则返回TRUE，否则返回FALSE */
   if(S.top==S.base)
     return TRUE;
   else
     return FALSE;
 }