Day5——数论

今天给我们讲课的是给我们讲搜索的那个老师。
早在他讲搜索的时候就经常提一些奇奇怪怪的数学。今天他给我们讲数论。虽然只是最简单的入门题，有点甚至连入门的难度都没有，然鹅，为什么还是这么难啊！！！
数论没啥好说的，直接看考题吧。

---

第一题数字游戏1

【问题描述】
给定一个正整数n，求最大的整数x，使得x < n，且digsum(x) =
digsum(n)−1，其中digsum(n)为n的各个位上数码之和，比如digsum(1234) =
1 + 2 + 3 + 4 = 10。
【输入格式】
多组数据，每行一个正整数n，字符串END表示输入结束。
【输出格式】
对每组数据输出一行表示答案。
【数据规模】
对于50%的数据，数据组数不超过10。
对于100%的数据：1 ≤ n ≤ 100000，数据组数不超过20000。
【算法思路】
将n的最低非0位-1即可，特别地，如果n是10的幂，那么所得的结果
是0。
代码：

#include
using namespace std;
int main()
{
    string s;
    int a,l,i,x;
    cin>>s;
    while (s!="END")//判断是否全部输入
    {
        a=0;
        l=s.size();
        for (i=0;i'0';//求数位和
            if (s[i]!='0') x=i;//记录不为零的最后一位
        }
        if (a==1) cout<1<//如果为十的整次幂，则输出0
          else
          {
            for (i=0;iif (i!=x) cout<else cout<'0'-1;//如果不是把不为零的最低位数字减一。
              }
            cout<cin>>s;
    } 
    return 0;
}

还可以简单一些：从低位到高位找不为零的数位，将其减一。如果为十的整次幂，则输出0。
代码：

#include
using namespace std;
int main()
{
    char ch[10]={};
    while(cin>>ch)
    {
        if(ch[0]=='E')
            break;
        int l=strlen(ch),p=l-1;
        while(ch[p]=='0')
            --p;
        if(p==0 && ch[p]=='1')
            puts("0");
        else
        {
            --ch[p];
            puts(ch);
        }
    }
}

---

第二题：石子游戏

【问题描述】
现在有一堆共n个石子，小A和小B两人轮流从中取石子（小A先取），
取到最后一个石子的人获胜。
但游戏不可能这么简单，所以有一个限制，每个人每次只能从中取1个
或者质数个石子，显然每次取出的石子个数不能超过当前堆中的石子个
数。
给定n，你的任务就是判断谁有必胜策略。
【输入格式】
第一行一个正整数T，表示数据组数。
接下来T组数据，每组数据一行一个正整数n。
【输出格式】
对每组数据，如果小A有必胜策略，那么就输出A，否则输出B。
【数据规模】
对于30%的数据，1 ≤ n ≤ 10。
对于60%的数据，1 ≤ n ≤ 1000。
对于100%的数据，1 ≤ T ≤ 1000, 1 ≤n≤ 10^9。

【算法思路】

注意到1,2,3都是可取的，而4不可取，故考虑模4分类。
接下来，注意到不能取走4的倍数个石子，并且可以取走模4余1,2,3个
石子，那么显然石子数是4的倍数时，小A必胜，否则小B必胜.
说实话代码真的很短。
代码：

#include
using namespace std;
int main()
{
    int T,n;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        puts(n%4 ? "A" : "B");
    }
}

---

第三题：数列计算

【问题描述】
已知一个n个整数的序列ai，将序列中任意两个位置不同的元素作差
（大的减小的），可以得到n * (n − 1)/2个数。
此外再给定一个类型k，你的任务根据k有所不同：
1、k= 1，则求这些数的和，结果模109 + 7。
2、k = 2，则将这些数各自平方再求和，结果模10^9 + 7。
【输入格式】
第一行为一个正整数T，表示数据组数。
接下来T组数据，每组数据第一行有两个正整数n, k，接下来一行n个
整数ai。
【输出格式】
对每组数据输出一行表示答案。
【样例输入】
2
5 1
3 5 1 2 4
5 2
3 5 1 2 4
【样例输出】
20
50
【样例解释】
输入数据中对应的10个数分别为2 2 1 1 4 3 1 1 3 2，和为20，各自平方
后结果为4 4 1 1 16 9 1 1 9 4，和为50。

因为数据规模较大，请使用stdio.h中的scanf和printf函数进行输入输出。
数列计算
【算法思路】
对于k = 1的情况，只要求每个数作为被减数和减数出现在了多少个数
里，而这只需要将原序列从小到大排序即可立即求出。
对于k = 2的情况，将(ai − aj)^2展开成ai^2 + aj^2 + 2aiaj，分为平方部
分ai^2与两两乘积部分aiaj。
注意到，两两之差的平方和是(n−1)倍的ai^2之和，再减去两倍的aiaj的
和，前一部分可以很方便地求出，而后一部分我们考虑ai之和进行平方，
这等于一倍的ai^2之和再加上两倍的aiaj的和，于是我们就可以得到aiaj之
和，从而求出答案。
代码：
#include
using namespace std;
const int N=50050,mod=1000000007;
int n,k,a[N]={};
int main()
{
int T=1;
scanf("%d",&T);
while(T--)
{
scanf("%d%d",&n,&k);
for(int i=1;i<=n;++i)
scanf("%d",a+i);
long long ans=0;
if(k==1)
{
sort(a+1,a+n+1);
for(int i=1;i<=n;++i)
(ans+=(mod+a[i])*1ll*((i-1)+mod-(n-i))%mod)%=mod;
}
else
{
long long sqrsum=0,sumsqr=0;
for(int i=1;i<=n;++i)
{
(sqrsum+=a[i]*1ll*a[i])%=mod;
(sumsqr+=mod+a[i])%=mod;
}
sumsqr=sumsqr*sumsqr%mod;
ans=(n*sqrsum+mod-sumsqr)%mod;
}
printf("%d\n",(int)ans);
}
}

---

第四题：纸张折叠

【问题描述】
有一张n个方格子的纸条，格子上无序地写着1到n这n个数字，每个数
字都恰好出现一次，每个格子一个数字。
现在沿着格子的边线折纸，可以将纸条折成一个小方块（正面看去只
有一个格子）。这样n个数字的方格就竖直地排列起来，如图所示：

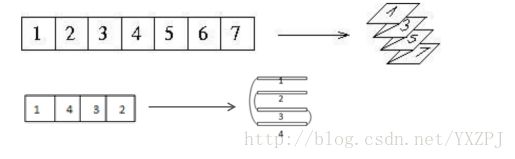
现在给定该纸条，判断是否能通过折纸使得这些方格上的数字从上到
下的排列正好是1到n（无论正反）。例如上图就是两个可行的例子（7个格
子的纸条和4个格子的纸条），若能，输出YES，否则输出NO。
【输入格式】
第一行一个正整数T，表示数据组数。
接下来T组数据，每组数据第一行有一个正整数n，表示数据组数，接
下来一行n个数，从左到右描述纸条上每格的数字。
【输出格式】
对每组数据输出一行，表示答案。
【样例输入】
2 3
2 1 3
4
1 3 4 2
【样例输出】
YES
NO

数据规模较大，请使用stdio.h中的scanf和printf函数进行输入输出。
纸张折叠
【算法思路】
从纸条的第一个格子开始，直接尝试折出所需要的形状。
参考题目中配图的下面那张纸带，折纸从1开始，1在一侧向4连边（对
应1与4的公共边），4在另一侧向3连边（对应4与3的公共边），3接着又换回
原来这侧向2连边（对应3与2的公共边），结束，折纸过程中所有边不相交，
故可行，同时我们也就得到了折纸方案。
具体到代码实现上，就是考虑相邻两个数所表示的n − 1个区间
（即[1,4],[3,4],[2,3]），将这些区间交替分为两组（即[1,4],[2,3]一组，[3,4]一
组），如果每组内部任意两个区间都只有不相交或包含关系的话，那么就可
行，否则不可行。
为了在n = 10^5时仍能高效地进行上述判断，可以使用各种高级数据结
构完成，也可采用以下方法：
将区间组内所有端点从左到右排序，并存储每个右端点所对应的左端
点，然后从左到右扫描端点并维护左端点栈：
1、如果当前端点是左端点，就将其压入栈。
2、如果是右端点那么就判断当前栈顶的左端点是否与该右端点对应，
对应则弹出栈顶并继续，不对应的话，则这些区间组就不符合我们所要的
条件。
如果成功扫描完了所有端点，那么这个区间组就是符合条件的。
利用区间端点均在[1,n]内的性质，该算法可以做到O(n)，如果暴力点
就O(n log n)，仍然可以通过。
代码：

#include
using namespace std;
const int N=100100;
int n,a[N]={},e[N]={},s[N]={};
bool check(int _)
{
    fill(e+1,e+n+1,0);
    for(int i=_;i+1<=n;i+=2)
    {
        int l=min(a[i],a[i+1]), r=max(a[i],a[i+1]);
        e[l]=-1, e[r]=l;
    }
    int top=0;
    for(int i=1;i<=n;++i)
    {
        if(e[i]<0)
            s[++top]=i;
        if(e[i]>0)
        {
            if(s[top]!=e[i])
                return false;
            --top;
        }
    }
    return true;
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        for(int i=1;i<=n;++i)
            scanf("%d",a+i);
        puts(check(1) && check(2) ? "YES" : "NO");
    }
}