Opencv计算机视觉之路(三)——图像处理(一)傅里叶变换

计算机视觉系列：傅里叶变换

——————————————————————————

1. 1. 傅里叶变换简介

    Joseph Fourier是一位18世纪的法国数学家，在数学领域，他认为一切事物均可以用波形来描述，所有观察到的波形也可以有一系列的简单的且频率不同的正弦曲线相加得到，也就是说，人们看到的波形是由多个波形相加得到的。

    当我们看到图像中哪些区域的信号变化特别强烈，哪些区域的信号变化不是很强烈，从而可以标记和区分噪声区域、感兴趣区域、前景、背景等。原始图像由许多频率组成，便可以分离这些频率来理解图像和提取感兴趣区域等，介绍傅里叶变换之前，先引入几个基本概念，以及推荐一篇知乎，看了这篇知乎后，我才茅塞顿开，应作者要求，还是转一下吧。傅里叶掐死教程

1.1 1.1 时域

    从我们出生，我们看到的世界都以时间贯穿，花开花落、生老病死、云彩的移动都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。

1.2 1.2 频域

    如果换一个角度观察世界，这个世界并没有发生变化。为什么呢，原因就是，观察的角度是频域，而不是时域。好，来介绍下什么是频域。以化学反应为例子：

NaOH+HCl=NaCl+H2O N a O H + H C l = N a C l + H 2 O

    显而易见，随着时间的推移，氢氧化钠与盐酸最终变成了氯化钠和水，在时域的角度，反应物发生了变化。在频域的角度呢， Na+ N a + 还是 Na+ N a + ，氢原子还是氢原子，本质并没有发生变化，这就是频域角度的分析。

    而贯穿时域与频域的方法之一，就是传中说的傅里叶分析。傅里叶分析可分为傅里叶级数（Fourier Serie）和傅里叶变换(Fourier Transformation)。

    介绍至此，在返回傅里叶大佬的思想。你眼中看似落叶纷飞变化无常的世界，实际只是躺在上帝怀中一份早已谱好的乐章。抱歉，这不是一句鸡汤文，而是黑板上确凿的公式：傅大佬告诉我们，任何周期函数，都可以看作是不同振幅 A A ，不同相位 ψ ψ 正弦波的叠加。

                                                             本小节结束
—————————————————————————————————————————————————————–

2. 2. 傅里叶眼里的时域和频域

2.1 2.1 频域坐标

    如果我说我能用前面说的正弦曲线波叠加出一个带90度角的矩形波来，你会相信吗？你不会，就像当年的我一样。但是看下图：

    中间那部分在逐渐的向正方形逼近，可能是我选取的波形函数不好，导致的效果也不是很好，但是能看出大体情况来，说明了什么？弯的终究会被掰直。

    不仅仅是矩形，你能想到的任何波形都是可以如此方法用正弦波叠加起来的。这是没有接触过傅里叶分析的人在直觉上的第一个难点，但是一旦接受了这样的设定，游戏就开始有意思起来了。图用matlplotlib画的，不放代码了，算了还是放吧。

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-10, 10, 1000)
a = np.cos(x)
b = a + np.cos(3 * x)
# d = np.log(x)
c = b + np.cos(7 * x)
d = c - np.cos(10 * x)
plt.subplot(2, 2, 1)
plt.plot(x, a, label='$cos(x)$', color='green', linewidth=1)
plt.title("cosx")
plt.xlim(-2, 2)
plt.ylim(-3, 3)

plt.subplot(2, 2, 2)
plt.plot(x, b, label='$cos(x)+cos(3x)$', color='red', linewidth=1)
plt.title("cosx+cos(3x)")
plt.xlim(-2, 2)
plt.ylim(-3, 3)


plt.subplot(2, 2, 4)
plt.plot(x, d, label='$cos(x)+cos(3x)+cos(7x)$', color='blue', linewidth=1)
plt.title("cosx+cos(3x)+cos(7x)-cos(10x)")
plt.xlim(-2, 2)
plt.ylim(-3, 3)

plt.subplot(2, 2, 3)
plt.plot(x, c, label='$cos(x)+cos(3x)+cos(7x)$', color='black', linewidth=1)
plt.title("cosx+cos(3x)+cos(7x)")
plt.xlim(-2, 2)
plt.ylim(-3, 3)

plt.show()

2.1 2.1 时域坐标

    如果把上面的四个函数排列开来，会得到什么效果呢？把四个波形函数放在如下所示的卡槽内，一号卡槽放一个函数，二号卡槽放一个函数，具体放哪个函数没有关系：

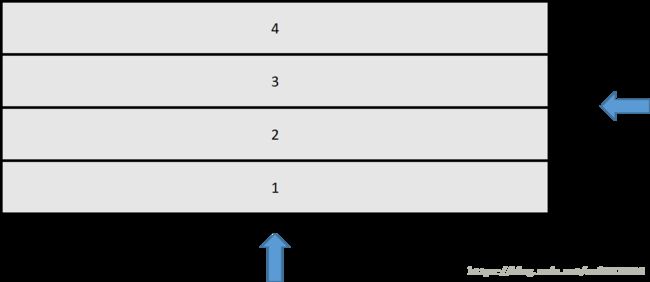
    从下面箭头所指的方向看去，会看到四个波形叠加的效果，就是前文提到的矩形，这就是时域的坐标轴；从右边所指的方向看去，会看到什么呢？会看到四条长短不一的直线，也就是那四个函数的振幅 A A 的大小，这就是频域的坐标轴。

    总结一下，频域坐标轴：函数随着时间的变化而变化；时域坐标轴：函数始终是这个函数，它本身没有变化。似乎终于讲明白了频域和时域，以及如何对应到傅里叶中，如果没看懂，那么就看我前文提到的那个博客，他画的图比我画的好看的多的多的多。
                                                             本小节结束
—————————————————————————————————————————————————————–

3. 3. 傅大佬变换

    傅里叶级数的本质是将一个周期的信号分解成无限多分开的（离散的）正弦波，公式如下， O O 表示观察信号， ω ω 表示频率， ϕ ϕ 表示相位， A A 表示振幅。但是宇宙变换似乎并不是周期的，任何常见事物的变化似乎也不是周期的，比如小姐姐每天的行程如果是周期的，那是不是太好下手了，这样就违背了自然规律。

f(O)=A1sin(ω1x+ϕ1)+A2sin(ω3x+ϕ2)+...+Ansin(ωnx+ϕn) f ( O ) = A 1 sin ⁡ ( ω 1 x + ϕ 1 ) + A 2 sin ⁡ ( ω 3 x + ϕ 2 ) + . . . + A n sin ⁡ ( ω n x + ϕ n )

    那有该如何处理这类问题，是否有一种数学工具将连续非周期信号变换为周期离散信号呢？比如追小姐姐呢？抱歉，真没有。那么傅大佬变化到底干嘛呢？当然是贯穿时域和频域的一种分析手段，实际上是对一个周期无限大的函数进行变换，将一个时域非周期的连续信号，转换为一个在频域非周期的连续信号：扯淡了半天，终于能到重点了。

    举个通俗的例子，钢琴(撑住，别乱，总感觉我的例子越举越混乱)。对于我这种没有音乐细胞的人而言，钢琴就是在键盘上按几下，然后发出声音。按键有重音，有轻音，按速有慢有快，放个图醒醒混乱的脑子以及形象的说明一下。

    时域：离散的按键信号变成了连续的信号，就是动听的音乐。

    频域：每一次的震动连续起来也就成了连续的信号，大家应该可以理解如何从离散谱变成了连续谱的了吧？原来离散谱的叠加，变成了连续谱的累积，所以在计算上也从求和符号变成了积分符号。（当然，这两个连续的函数是不一样的，就是紫色的那个，我只是懒的画新的了。）傅里叶的深度应用准备在暑期更新了，现在理解基本概念就好。

                                                本小节结束
—————————————————————————————————————————

3. 3. 傅大佬变换在图像处理中的应用

    好了，有了上述的概念，再来看看图像的傅里叶变换，上述举得例子是一维信号的傅里叶变换，并且信号是连续的。我们知道图像是二维离散的，连续与离散都可以用傅里叶进行变换，那么二维信号无非就是在 x x 方向与 y y 方向都进行一次一维的傅里叶变换得到。这么看来，可以想象，它的时域构成就是一个网格矩阵了，横轴从 1 1 到 n n ，纵轴也是这样，所有图像的时域构成都认为是这样的。频域呢，当然同上，也会得到有关频域的网格矩阵。

    下面看看二维傅里叶变换，一个图像为 M×N M × N 的图像 f(x,y) f ( x , y ) 进过离散傅里叶变换得到 F(u,v) F ( u , v ) ，那么一般的公式为：

F(u,v)=∑x=0m∑y=0nf(x,y)e2π⋅t F ( u , v ) = ∑ x = 0 m ∑ y = 0 n f ( x , y ) e 2 π ⋅ t

t=(uxm+vyn) t = ( u x m + v y n )

    那么这个公式表示了什么意思呢，以下方图像为例。两个求和号对图像进行遍历， f(x,y) f ( x , y ) 取出原像素的数值，当 x=0 x = 0 ，(横轴不动)，对 y y 进行遍历时， t t 的后一项表示变换前像素的位置比例与变换后的位置相乘，映射到新的位置，且能够反映像素延 y y 方向距离的差异，越靠后的像素( y y 越大) t t 值越大，即 t t 能够反映出不同位置(纵轴)像素之间的差异；前一项含义为保留像素相对位置(横轴)的信息(遍历 y y 时为常数)， 2π 2 π 为修正参数。因此，对于 f(x,y) f ( x , y ) 而言，this is 时域，对于得到的 F(u,v) F ( u , v ) 而言，this is 频域。why？因此你无法从一个波中分解出他原来众多的波形，只能用 F(u,v) F ( u , v ) 的形式去反应频域的趋势，在深入分析一下，脑补频域轴， f(x,y) f ( x , y ) 大的地方 F(u,v) F ( u , v ) 也大，而且还能根据位置因素对其分解，对于靠后的像素， f(x,y) f ( x , y ) 大， t t 也大，分解出来的波形在频域的投影也大，因此， F(u,v) F ( u , v ) 是对图像提取频域的操作。

3.1 3.1 频域变换

    下面通过傅里叶变化来介绍图像的幅度普，幅度普呈现了原始图像在变化方面的一种表示：图像最明亮的像素放到中央，然后逐渐变暗，在边缘上的像素最暗，这样可以发现图像中亮、暗像素的百分比。（即为频域中的振幅 A A 的强度）

    在opencv环境中，许多算法实现了处理图像的功能，这些算法在numpy中也有实现，且更容易使用。首先使用Numpy做频率变换，Numpy有一个FFT(快速傅里叶变换)包来完成这个工作，np.fft.fft2()为我们提供了一个复杂数组的频率转换，即一幅图像的离散傅里叶变换。

    它的第一个参数是输入图像，它是灰度图像。第二个参数是可选的，它决定了输出数组的大小。如果它大于输入图像的大小，则输入图像在计算FFT之前填充了0。如果它小于输入图像，输入图像将被裁剪。如果没有参数传递，输出数组的大小将与输入相同。

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('test.jpg', 0) #直接读为灰度图像
f = np.fft.fft2(img)            #做频率变换
fshift = np.fft.fftshift(f)     #转移像素做幅度普

s1 = np.log(np.abs(fshift))#取绝对值：将复数变化成实数取对数的目的为了将数据变化到0-255
plt.subplot(131)
plt.imshow(img, 'gray')
plt.title('original')

plt.subplot(132)
plt.imshow(s1,'gray')
plt.title('center')

plt.show()

    得到的结果如下：

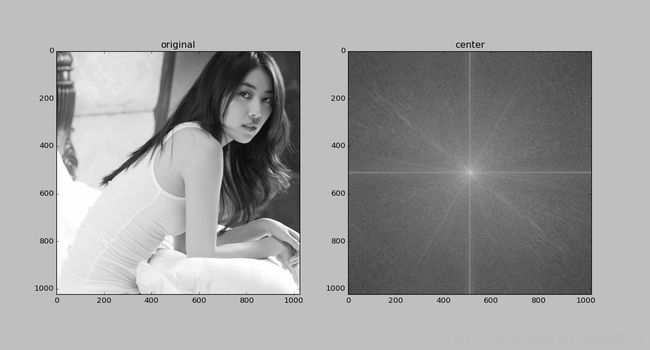
    也许你会问为什么用 log l o g 函数去映射，而不是采取以下的归一化的形式去用，我看了下矩阵的元素，绝大多数的像素数值都很小，如果采用以下的形式去归一化，绝大多数的数值均很小，会得到一个黑色的图像，归一化的东西本文不在详细介绍，归一化这种东西本来就是建模里面一个不好掌控的度。

X−XminXmax−X X − X m i n X m a x − X

    你可以在中心看到更多的白色区域，表示低振幅的波占到了多数，高振幅的波占少数，而且说明了波的整体频率偏低。为什么呢，先引入一个概念：在波形的调控中，需要较多的直线和近似直线的波来调整。低频波越多，也就是有较多的波近似于直线，也就是，这些波的频率很慢， ω ω 很小。

                                                             本小节结束
—————————————————————————————————————————————————————–

1.1 1.1 时域变换

    下一步进行时域变换，比如高通滤波器。为此，你只需用一个矩形窗口大小来移除低频部分(频率 ω ω 越大，震动越明显)，即保留下图像中最有用的信息。那么图像中的什么位置的频率比较高呢，显而易见，边界处。为什么呢，在非交界处，你的波可以慢慢悠悠的抖动来显示信息；在交界处，没有快速的抖动，怎么去显示差异呢？

1.1.1 1.1.1 高通滤波器介绍

    高通滤波器(HPF)是检测图像的某个区域，然后根据像素与周围像素的差值来提升该像素亮度的滤波器。

    以如下的核(kernal)为例，

[[0, -0.25, 0],
[-0.25, 1, -0.25],
[0, -0.25, 0]]

    核是一组权重的集合，他会应用与原图像的一个区域，并生成目标区域的一个像素。比如，大小为7的核意味着(7x7)个原图像的像素会产生目标图像的一个像素。可以将核视为一个窗口，这个窗口在原图像上移动时，覆盖区域的像素会按着某种形式透过此窗口，形成一个像素点；随着窗口的不断移动，形成最终的目的图像。

    在计算完中央像素与周围临近像素的亮度差值以后，如果亮度变化很大，中央像素的亮度会增加，这在边缘检测中十分有效，下一篇文章将会介绍边缘检测。高通滤波器有一种称为半径的属性，决定多大面积的临近像素参与滤波运算，也就是你设置的kernel的一维长度。

    举一个例子说明以上的理论。随意设置个矩阵如，当然不是随意的，很明显是边缘交界处的像素矩阵:

⎡⎣⎢⎢⎢⎢⎢⎢00000013501001001001001000246000000⎤⎦⎥⎥⎥⎥⎥⎥ [ 0 0 100 0 0 0 1 100 2 0 0 3 100 4 0 0 5 100 6 0 0 0 100 0 0 ]

    与之前给出的核进行卷积运算，对于矩阵的 (3,3) ( 3 , 3 ) 位置的元素而言，它的运算步骤是

0×1+(−0.25)×100+0×2+(−0.25)×3+100×1+4×(−0.25)+5×0+100×(−0.25)+0×6=48.25 0 × 1 + ( − 0.25 ) × 100 + 0 × 2 + ( − 0.25 ) × 3 + 100 × 1 + 4 × ( − 0.25 ) + 5 × 0 + 100 × ( − 0.25 ) + 0 × 6 = 48.25

    脑补一下这个矩阵的卷积结果，边界的值越来越大，旁边的值越来越小，也就是，能够检测边缘。

    实战一下，在设置核后，与读入的图像进行卷积运算，卷积运算可以使用cv2提供的函数实现。

import cv2
import numpy as np
import matplotlib.pyplot as plt

kernel_9 = np.array([[-1, -1, -1],
                     [-1, 8, -1],
                     [-1, -1, -1]])

kernel_25 = np.array([[-1, -1, -1, -1, -1],
                      [-1, 1, 2, 1, -1],
                      [-1, 2, 4, 2, -1],
                      [-1, 1, 2, 1, -1],
                      [-1, -1, -1, -1, -1]])

img = cv2.imread('test.jpg')
ndimg = np.array(img)

k3 = cv2.filter2D(ndimg, -1, kernel_9)      #convolve calculate 
k5 = cv2.filter2D(ndimg, -1, kernel_25)     #the second parameters measns the deepth of passageway.
#such as cv2.CV_8U means every passageway is 8 bit.
#-1 means the passageway of the source file and the object file is equal.
plt.subplot(131)
plt.imshow(img)
plt.title("source image")

plt.subplot(132)
plt.imshow(k3)
plt.title("kernel = 3")

plt.subplot(133)
plt.imshow(k5)
plt.title("kernel = 5")

plt.show()

    得到的结果如下：

    与高通滤波器相反的还有低通滤波器(LPF)，低筒滤波器与高通滤波器相反，当一个像素与周围像素的插值小于一个特定值时，平滑该像素的亮度，用于去燥和模糊化，比如PS软件中的高斯模糊，就是常见的模糊滤波器之一，属于削弱高频信号的低通滤波器。

    做一个简单的低通滤波器

import cv2
import numpy as np
import matplotlib.pyplot as plt

kernel_25h = np.array([[-1, -1, -1, -1, -1],
                      [-1, 1, 2, 1, -1],
                      [-1, 2, 4, 2, -1],
                      [-1, 1, 2, 1, -1],
                      [-1, -1, -1, -1, -1]])

kernel_25l = np.array([[0.04, 0.04, 0.04, 0.04, 0.04],
                      [0.04, 0.04, 0.04, 0.04, 0.04],
                      [0.04, 0.04, 0.04, 0.04, 0.04],
                      [0.04, 0.04, 0.04, 0.04, 0.04],
                      [0.04, 0.04, 0.04, 0.04, 0.04]])

img = cv2.imread('test.jpg')
ndimg = np.array(img)

k3 = cv2.filter2D(ndimg, -1, kernel_25h)
k5 = cv2.filter2D(ndimg, -1, kernel_25l)

plt.subplot(131)
plt.imshow(img)
plt.title("source image")

plt.subplot(132)
plt.imshow(k3)
plt.title("kernel5hpf")

plt.subplot(133)
plt.imshow(k5)
plt.title("kernel5lpf")
plt.show()

    结果如下：中间的图为高通滤波，最右方的图为模糊化后的。

                                                             本小节结束
—————————————————————————————————————————————————————–