数据结构(链表、链栈、链队列、二叉树、图)
本文用于总结数据结构(链表、链栈、链队列、二叉树、图)的创建方式与遍历方式!!!
本目录代码已上传至github中!!!
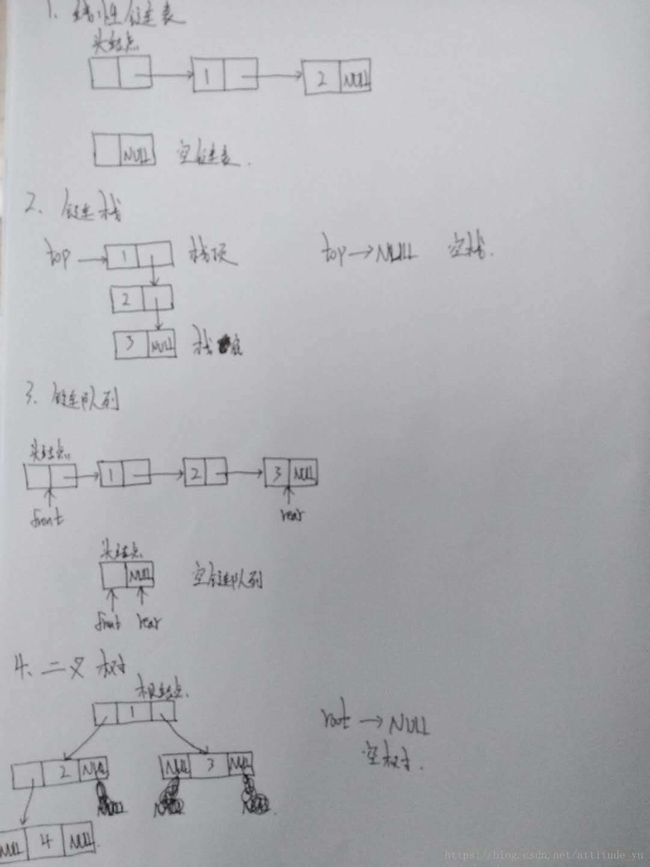
1. 链表
1. 线性表顺序存储和链式存储的优缺点?
顺序存储:
a.不需要增加额外的存储空间,快速存取指向位置的元素;
b.在插入和删除过程中,需要移动大量元素;
c.需要预先分配存储空间;
链式存储:
a.插入删除操作时间为O(1);
b.用任意位置的存储单元存储元素;
#include
using namespace std;
typedef struct Node
{
int data;
Node *next;
}Node;
//头插法创建链表
void head_insert_create_list(Node *L, int n)
{
//创建节点
for (int i = 0; i < n; i++)
{
Node *new_node = new Node;
new_node->data = i;
new_node->next = L->next;
L->next = new_node;
}
}
//尾插法创建链表
void tail_insert_create_list(Node *L, int n)
{
//初始化尾部节点为头节点
Node *r = L;
for (int i = 0; i < n; i++)
{
Node *new_node = new Node;
new_node->data = i;
r->next = new_node;
//更新尾节点为新节点
r = new_node;
}
//尾节点的指针域为空
r->next = NULL;
}
//在第i个位置后插入节点
void insert_node(Node *L, int i, int num)
{
Node *node = L->next;
int j = 1;
//找到第i个节点
while (node&&j < i)
{
node = node->next;
++j;
}
//鲁棒性设计
if (!node || j > i)
return;
Node *new_node = new Node;
new_node->data = num;
new_node->next = node->next;
node->next = new_node;
}
//在第i个位置删除节点
void delete_node(Node *L, int i)
{
Node *node = L->next;
int j = 1;
//找到第i个节点的上一个节点
while (node&&j < i-1)
{
node = node->next;
++j;
}
//鲁棒性设计
if (!node->next || j > i)
return;
Node *delete_node = node->next;
node->next = delete_node->next;
free(delete_node);
}
//遍历链表
void print_list(Node *L)
{
//第一个节点
Node *node = L->next;
while (node)
{
cout << node->data << " ";
node = node->next;
}
cout << endl;
}
void main()
{
//创建头节点
Node *L = new Node;
L->data = 5;//链表长度
L->next = NULL;
//head_insert_create_list(L, L->data);
//print_list(L);
tail_insert_create_list(L, L->data);
print_list(L);
insert_node(L, 2, 6);
print_list(L);
delete_node(L, 3);
print_list(L);
} 2. 链栈
栈是后进先出的线性表,其仅可以在表尾进行删除和插入操作。
#include
using namespace std;
typedef struct Node // 定义链栈节点
{
int data;
Node *next;
}Node;
typedef struct Stack
{
Node *top; // 定义链栈栈顶节点
int count;
}Stack;
//创建链栈
void create_stack(Stack *S, int n)
{
Node *node = S->top;
for (int i = 0; i < n; i++)
{
Node *new_node = new Node;
new_node->data = i;
new_node->next = S->top;
S->top = new_node;
}
}
//插入栈节点
void insert_node(Stack *S, int data)
{
Node *new_node = new Node;
new_node->data = data;
new_node->next = S->top;
S->top = new_node;
S->count++;
}
//删除栈节点
void pop_node(Stack *S)
{
//鲁棒设计
if (S->top == NULL)
return;
Node *top_node;
top_node = S->top;
S->top = top_node->next;
cout << "删除节点值是: " << top_node->data << endl;
free(top_node);
}
//打印栈节点
void print_stack(Stack *S)
{
Node *node = S->top;
cout << "打印栈节点:";
while (node)
{
cout << node->data << " ";
node = node->next;
}
}
void main()
{
//创建空栈
Stack *S = new Stack;
S->top = NULL;
S->count = 0;
create_stack(S, 5);
print_stack(S);
insert_node(S, 5);
print_stack(S);
pop_node(S);
}
3. 链队列
队列是先进先出的线性表,其在队尾进行插入操作,在队首进行删除操作。
#include
using namespace std;
typedef struct Node //定义队列节点
{
int data;
Node *next;
}Node;
typedef struct Queue // 定义链队列的首尾指针,其指向的是首尾节点
{
Node *front;
Node *rear;
}Queue;
//创建队列
void create_queue(Queue *Q, int n)
{
for (int i = 0; i < n; i++)
{
Node *new_node = new Node;
new_node->data = i;
new_node->next = NULL;
Q->rear->next = new_node;//队尾插入节点
Q->rear = new_node;
}
}
//队尾插入节点
void insert_node(Queue *Q, int num)
{
Node *new_node = new Node;
new_node->data = num;
new_node->next = NULL;
Q->rear->next = new_node;
Q->rear = new_node;
}
//队首删除节点
void delete_node(Queue *Q)
{
//鲁棒性设计
if (Q->front == Q->rear)
return;
Node *delete_node;
//获得第一个节点
delete_node = Q->front->next;
Q->front->next = delete_node->next;
cout << "删除节点的值:" << delete_node->data << endl;
free(delete_node);
}
void main()
{
//创建空队列 队首队尾指针指向头节点
Queue *Q = new Queue;
Node *head_node = new Node;
head_node->next = NULL;
head_node->data = 5;
Q->front = head_node;
Q->rear = head_node;
create_queue(Q, 5);
delete_node(Q);
delete_node(Q);
insert_node(Q, 3);
delete_node(Q);
} 4. 二叉树
1. 二叉树顺序存储和链式存储的对比
二叉树的顺序存储是节点的下标对应数组的索引下标来存储的。对于深度树来说,若其节点数不多时,
由于需要以完全二叉树的规模进行存储,此时会造成内存空间的浪费。
二叉树的链式存储是为每个节点设置数据域和两个指针域,若节点的左右子树不存在时,此时指针域
为空,即没有内存的分配,其具有线性表链式存储的特点。
2. 二叉树的创建
递归以前序遍历的方式创建节点,指定左右子节点为空时的输入值。
3. 二叉树的遍历
递归打印节点的值,打印的位置不同,遍历的方式也就不同。
#include
#include
using namespace std;
typedef struct Node
{
int data;
Node *lchild;
Node *rchild;
}Node;
//创建二叉树
Node * create_binary_tree(int depth, string pos)
{
cout << "the depth is : " << depth << " the pos is : " << pos << endl;
int data;
cin >> data;
if (data == 0)
return NULL;
Node * new_node = new Node;
new_node->data = data;
new_node->lchild = create_binary_tree(depth + 1, "lchild");
new_node->rchild = create_binary_tree(depth + 1, "rchild");
return new_node;
}
//前序遍历二叉树
void pre_order_print(Node *root)
{
if (root == NULL)
return;
cout << "the data is : " << root->data << " ";
pre_order_print(root->lchild);
pre_order_print(root->rchild);
}
//中序遍历二叉树
void mid_order_print(Node *root)
{
if (root == NULL)
return;
mid_order_print(root->lchild);
cout << "the data is : " << root->data << " ";
mid_order_print(root->rchild);
}
//后序遍历二叉树
void last_order_print(Node *root)
{
if (root == NULL)
return;
last_order_print(root->lchild);
last_order_print(root->rchild);
cout << "the data is : " << root->data << " ";
}
void main()
{
Node * root = new Node;
root = create_binary_tree(1, "root");
pre_order_print(root);
cout << endl;
} 5. 图
1. 图的邻接矩阵存储和邻接表存储
和线性表问题一样,链式存储比顺序存储更节约内存。
2. 邻接表存储
图的顶点用数组存储(顶点域和指针域),邻接点用链表存储(顶点域、权重域、指针域)
3. 深度优先遍历
类似于树的前序遍历,从指定顶点开始,从其边表顶点开始遍历递归,并设置已访问顶点的标志位,直至所有顶点都被访问到。
4. 广度优先遍历
类似于树的层序遍历(遍历邻接表的每行),从指定顶点表顶点开始,遍历每个顶点表顶点指向的边表顶点,
将访问过的顶点表顶点出队列,将未被访问过的顶点压入队列
#include
#include
using namespace std;
const int Maxsize = 10;
bool visited[Maxsize];
typedef struct EdgeNode//边表顶点
{
int data;
int weight;
EdgeNode *next;
}EdgeNode;
typedef struct VertexNode//顶点表顶点
{
int data;
EdgeNode *next;
}VertexNode,VertexList[Maxsize];
typedef struct Graph//无向图
{
VertexList vertex_list;
int vertex_num;//顶点数量
int edge_num;//边数量
}Graph;
//打印边表顶点信息
void print_edge_node(EdgeNode *node)
{
cout << "the data of edge node: ";
while (node)
{
cout << node->data << " ";
node = node->next;
}
cout << endl;
}
//创建无向图的邻接表
void create_graph(Graph *G)
{
cout << "the number of vertex node and edge : ";
cin >> G->vertex_num >> G->edge_num;
cout << G->vertex_num << " " << G->edge_num << endl;
//创建顶点表
for (int i = 0; i < G->vertex_num; i++)
{
G->vertex_list[i].data = i;
G->vertex_list[i].next = NULL;
}
//创建边表 假设无向图有5个顶点,则完全无向图有10条边
for (int j = 0; j < G->edge_num; j++)
{
int a, b;
cout << "from the vertex a to vertex b: ";
cin >> a >> b;
EdgeNode * e_node = new EdgeNode;
e_node->data = b;//邻接顶点是b
e_node->next = G->vertex_list[a].next;//头插法
G->vertex_list[a].next = e_node;
EdgeNode * e_node_ = new EdgeNode;
e_node_->data = a;//邻接顶点是a
e_node_->next = G->vertex_list[b].next;//头插法
G->vertex_list[b].next = e_node_;
}
}
//深度优先遍历 指定遍历起始点
void depth_first_search_core(Graph *G, int i)
{
visited[i] = true;
cout << G->vertex_list[i].data << " ";
EdgeNode *node;
node = G->vertex_list[i].next;
while (node)
{
//如果边表顶点未被访问过,则递归此顶点对应边表顶点
if (!visited[node->data])
depth_first_search_core(G, node->data);
//递归返回后,继续遍历边表顶点
node = node->next;
}
}
void depth_first_search(Graph *G)
{
//初始化访问标志位
for (int i = 0; i < G->vertex_num; i++)
visited[i] = false;
cout << "the result of depth first search is ";
depth_first_search_core(G, 0);
cout << endl;
}
//广度优先遍历
void bread_first_search_core(Graph *G, int i)
{
queue Q;
EdgeNode *e_node;
if (!visited[i])
{
visited[i] = true;
cout << G->vertex_list[i].data << " ";
//起始顶点入队列
Q.push(i);
while (!Q.empty())
{
//更新边表顶点
i = Q.front();
//顶点表顶点出队列
Q.pop();
e_node = G->vertex_list[i].next;
while (e_node)
{
if (!visited[e_node->data])
{
visited[e_node->data] = true;
cout << G->vertex_list[e_node->data].data << " ";
//边表顶点入队列
Q.push(e_node->data);
}
e_node = e_node->next;
}
}
}
}
void bread_first_search(Graph *G)
{
//初始化访问标志位
for (int i = 0; i < G->vertex_num; i++)
visited[i] = false;
cout << "the result of bread first search is ";
bread_first_search_core(G, 0);
cout << endl;
}
void main()
{
Graph graph = { NULL, 0, 0 };
Graph *G = &graph;
create_graph(G);
for (int i = 0; i < G->vertex_num; i++)
{
EdgeNode *node = G->vertex_list[i].next;
print_edge_node(node);
}
depth_first_search(G);
bread_first_search(G);
} 参考资料:
1.《大话数据结构》