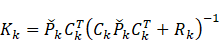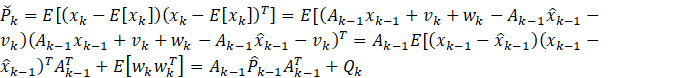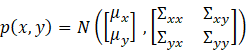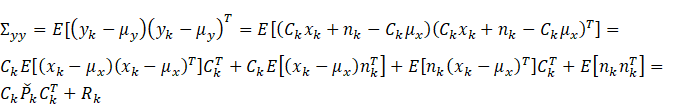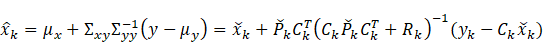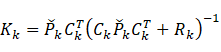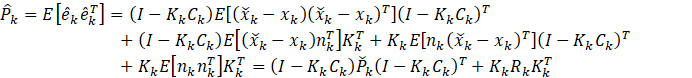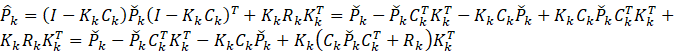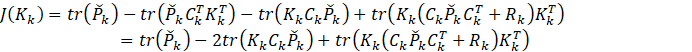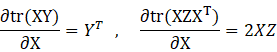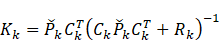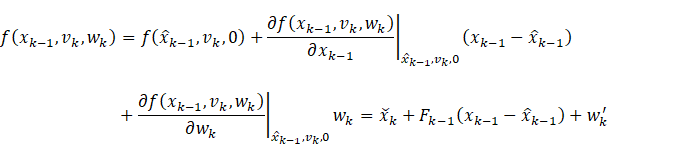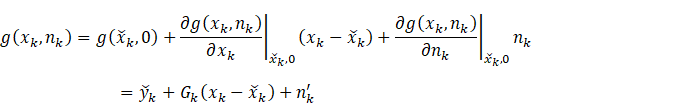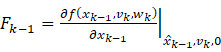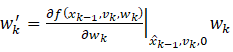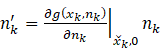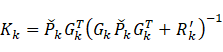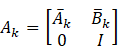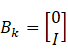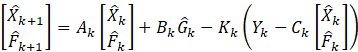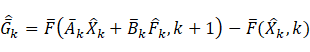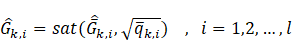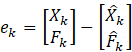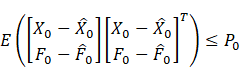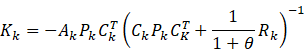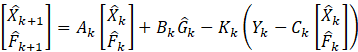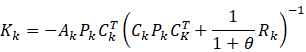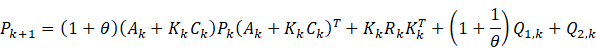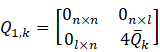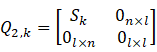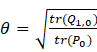卡尔曼滤波学习总结
卡尔曼滤波学习总结
本文内容主要基于《State Estimation for Robotics》,同时参考了一些其他教程,详见文末参考文献。所有内容仅代表个人理解,不当之处请批评指正。
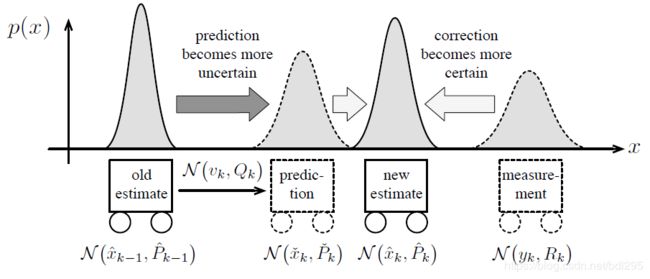
卡尔曼滤波是对系统状态进行估计的一种方法,大体过程用一句话概括就是:根据系统模型和现有状态预测下一步的状态,然后根据实际测量结果进行校正。
考虑离散时间线性时变系统,定义系统模型如下
运动模型:![]()
观测模型:![]()
各个变量的涵义如下,除输入![]() 为已知确定量外,其余均为随机变量,并且假设所有的噪声变量以及初始状态两两互不相关(包括同一噪声量在不同时刻的值)
为已知确定量外,其余均为随机变量,并且假设所有的噪声变量以及初始状态两两互不相关(包括同一噪声量在不同时刻的值)
系统状态:![]()
初始状态:![]()
输入: ![]()
过程噪声:![]()
测量值: ![]()
测量噪声:![]()
在这些变量中,我们能够直接得到的量有:系统初始状态![]() ,输入
,输入![]() ,测量值
,测量值![]() ,目的是要根据这些量来估计系统状态
,目的是要根据这些量来估计系统状态![]() 。
。
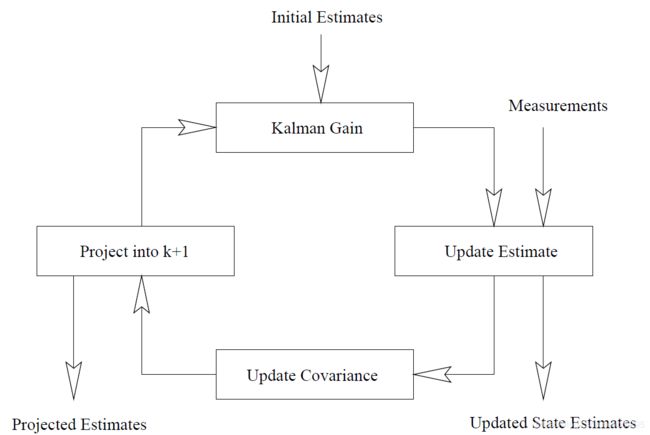
先给出卡尔曼滤波的算法,其中预测值用![]() 表示,校正后的估计值用
表示,校正后的估计值用![]() 表示。
表示。
| 预测 |
|
| |
|
| 卡尔曼增益 |
|
| 校正 |
|
| |
图1 卡尔曼滤波算法流程
图2 预测和校正过程图解
1 卡尔曼滤波推导
下面分别从概率和控制的角度对卡尔曼滤波进行推导。
从概率的角度来看,卡尔曼滤波是贝叶斯滤波的一种,主要理论依据是贝叶斯定理。已知在![]() 时刻的先验知识为
时刻的先验知识为
![]()
对于![]() 时刻,首先根据系统运动模型加入输入
时刻,首先根据系统运动模型加入输入![]() 进行预测(相对于
进行预测(相对于![]() 时刻的条件概率仅多了条件
时刻的条件概率仅多了条件![]() )
)
![]()
其中
![]()
接下来是校正过程,即在获得测量值![]() 以后计算后验概率
以后计算后验概率![]()
此处要套用多元高斯分布中的一个结论,即若
则
![]()
那么根据系统观测模型,由于
其中
![]()
可得后验分布
![]()
其中
定义卡尔曼增益
则上面各式简化为
![]()
![]()
至此推导完毕。
从控制的角度来看,卡尔曼滤波器可以看作是一个状态观测器,用来重构系统的真实状态,观测器方程为
![]()
![]()
从观测器方程可以看出,![]() 时刻的状态估计量
时刻的状态估计量![]() 包含两部分,一部分是根据系统运动模型和
包含两部分,一部分是根据系统运动模型和![]() 时刻的估计量
时刻的估计量![]() 以及已知输入
以及已知输入![]() 计算得到的预测结果,用
计算得到的预测结果,用![]() 表示,即
表示,即
![]()
另一部分则是根据观测器预测输出和实际测量系统输出对重构状态进行校正。状态观测器设计即要确定观测器增益![]() ,采用最小化平方误差的原则进行设计即为卡尔曼滤波器,此时观测器增益
,采用最小化平方误差的原则进行设计即为卡尔曼滤波器,此时观测器增益![]() 称为卡尔曼增益。
称为卡尔曼增益。
利用![]() 将观测器方程进行简化
将观测器方程进行简化
![]()
定义误差为
![]()
即有
其中定义误差协方差矩阵为
![]()
![]()
继续将![]() 展开
展开
平方误差为
![]()
即
将![]() 关于
关于![]() 求导,利用以下结论
求导,利用以下结论
可得
![]()
令![]() 得
得
那么
![]()
最后还剩下误差协方差的递推公式,由于
![]()
![]()
至此推导完毕。
2 扩展卡尔曼滤波
由于卡尔曼滤波公式是在假设了系统是线性系统,并且所有噪声都是高斯分布得到的,所有适用范围也仅限于线性系统、高斯噪声。尤其是从上面的推导可以看出,![]() 和
和![]() 的计算公式均是由高斯分布的后验概率得到的。当噪声不是高斯分布,或者系统为非线性时,后验概率一般都不是高斯分布,因此卡尔曼滤波都不能直接应用。
的计算公式均是由高斯分布的后验概率得到的。当噪声不是高斯分布,或者系统为非线性时,后验概率一般都不是高斯分布,因此卡尔曼滤波都不能直接应用。
然而,实际系统很少能够真正满足线性、高斯噪声的条件,为了在实际中应用卡尔曼滤波,需要解决系统非线性和噪声分布的问题,由此衍生出来很多相关的滤波算法。将非线性系统进行局部线性化,同时保留高斯噪声的假设,得到的就是常见的扩展卡尔曼滤波;此外,还有保留高斯噪声假设但不进行线性化,取关键点进行变换的SigmaPoint卡尔曼滤波;不保留任何假设,直接对概率密度进行密集采样,用大量的采样点来表示概率分布的粒子滤波。
考虑非线性系统模型
运动模型:![]()
观测模型:![]()
分别对运动模型和观测模型进行一阶泰勒展开
其中
由此得到线性化的系统模型,加上高斯噪声的假设,类似地可得以下扩展卡尔曼滤波公式
'![]()
![]()
![]()
![]()
3 扩展状态卡尔曼滤波
扩展卡尔曼滤波在线性化的同时带来了一个很大的局限性,那就是需要保证初始误差和噪声干扰足够的小(因为是在![]() 和
和![]() 点进行泰勒展开),否则效果会很差甚至不能收敛。为了解决这个问题,扩展状态卡尔曼滤波通过引入“扩展状态观测器”实时地对非线性系统进行观测和补偿,减小系统模型不准确所带来的误差,将初始误差和噪声干扰足够小的条件放宽至有界,可以大大拓展卡尔曼滤波的应用范围。
点进行泰勒展开),否则效果会很差甚至不能收敛。为了解决这个问题,扩展状态卡尔曼滤波通过引入“扩展状态观测器”实时地对非线性系统进行观测和补偿,减小系统模型不准确所带来的误差,将初始误差和噪声干扰足够小的条件放宽至有界,可以大大拓展卡尔曼滤波的应用范围。
由前面的推导已经知道,卡尔曼滤波可以看成是一个按照最小化平方误差原则设计的状态观测器。在解决非线性系统以及不确定因素很大的系统控制问题中,中国科学院数学研究所的韩京清先生提出了自抗扰控制技术,将系统建模误差、未建模动态、系统模型变化等全部看作内部扰动,与作用到系统上的外部扰动一起,统一看作“总扰动”,并将总扰动作为系统状态的一部分即“扩展状态”,用状态观测器与系统真实状态一起进行观测,然后利用观测到的扩展状态(总扰动)对系统真实状态进行补偿[3]。基于自抗扰控制中扩展状态观测器的思想,[4]提出了扩展状态卡尔曼滤波。为了方便表述,以下变量符号与文献[4]保持一致,与上文有所不同。
首先将非线性系统表示为已知线性近似模型和非线性不确定因素两部分
![]()
其中![]() 为线性部分,
为线性部分,![]() 为非线性不确定部分,看作“总扰动”,但
为非线性不确定部分,看作“总扰动”,但![]() 、
、![]() 均为已知,且
均为已知,且![]() 有一个已知的近似模型
有一个已知的近似模型![]() ,
,![]() 以及下面的
以及下面的![]() 仍分别表示过程噪声和测量噪声,假设为两两互不相关的零均值高斯噪声。系统观测模型表示为线性模型
仍分别表示过程噪声和测量噪声,假设为两两互不相关的零均值高斯噪声。系统观测模型表示为线性模型
![]()
将![]() 作为扩展状态,以上系统表示为
作为扩展状态,以上系统表示为
针对上述模型设计扩展状态观测器
其中![]() 按照如下方式定义
按照如下方式定义
![]()
其中![]() ,并且对
,并且对![]() 有如下假设
有如下假设
![]()
那么
![]()
引入初始误差和噪声有界的假设
![]()
![]()
对![]() 进行展开并利用假设进行放缩,然后将其上界关于
进行展开并利用假设进行放缩,然后将其上界关于![]() 求导并令导数为零,可得(具体推导过程见论文)
求导并令导数为零,可得(具体推导过程见论文)
其中![]() 定义见下文。于是,扩展状态卡尔曼滤波完整过程如下
定义见下文。于是,扩展状态卡尔曼滤波完整过程如下
其中![]() 。
。
参考文献:
[1] Lacey T. Tutorial: The kalman filter[J]. Georgia Institute of Technology.
[2] Barfoot T D. State Estimation for Robotics[M]. Cambridge University Press, 2017.
[3] Han J. From PID to active disturbance rejection control[J]. IEEE transactions on Industrial Electronics, 2009, 56(3): 900-906.
[4] Bai W, Xue W, Huang Y, et al. On extended state based Kalman filter design for a class of nonlinear time-varying uncertain systems[J]. Science China Information Sciences, 2018, 61(4): 042201.