神经网络

1. 深度神经网络DNN

1.1 概念来源

1.1.1 起源

​ 神经网络技术起源于上世纪五、六十年代，当时叫感知机（perceptron），拥有输入层、输出层和一个隐含层。输入的特征向量通过隐含层变换达到输出层，在输出层得到分类结果。早期感知机的推动者是Rosenblatt。

​ 但是，Rosenblatt的单层感知机有一个严重得不能再严重的问题，即它对稍复杂一些的函数都无能为力（比如最为典型的“异或”操作）。

1.1.2 发展

​ 随着数学的发展，直到上世纪八十年代才被Rumelhart、Williams、Hinton、LeCun等人发明了多层感知机，多层感知机，就是有多个隐含层的感知机。多层感知机可以

​ 多层感知机可以摆脱早期离散传输函数的束缚，使用sigmoid或tanh等连续函数模拟神经元对激励的响应，在训练算法上则使用Werbos发明的反向传播BP算法。这时候，产生了神经网络的概念。神经网络的层数直接决定了它对现实的刻画能力。

​ 随着神经网络层数的加深，优化函数越来越容易陷入局部最优解，并且这个“陷阱”越来越偏离真正的全局最优。利用有限数据训练的深层网络，性能还不如较浅层网络。同时，另一个不可忽略的问题是随着网络层数增加，“梯度消失”现象更加严重。

1.1.3 形成

​ 2006年，Hinton利用预训练方法缓解了局部最优解问题，将隐含层推动到了7层[2]，神经网络真正意义上有了“深度”，由此揭开了深度学习的热潮。这里的“深度”并没有固定的定义——在语音识别中4层网络就能够被认为是“较深的”，而在图像识别中20层以上的网络屡见不鲜。为了克服梯度消失，ReLU、maxout等传输函数代替了sigmoid，形成了如今DNN的基本形式。单从结构上来说，DNN和多层感知机是没有任何区别的。

​ 值得一提的是，之后出现的高速公路网络（highway network）和深度残差学习（deep residual learning）进一步避免了梯度消失，网络层数达到了前所未有的一百多层（深度残差学习：152层）

1.2 典型网络模型

1.2.1 Stacked Auto-Encoder堆叠自编码器

​ 堆叠自编码器是一种最基础的深度学习模型，该模型的子网络结构自编码器通过假设输出与输入是相同的来训练调整网络参数，得到每一层中的权重。通过堆叠多层自编码网络可以得到输入信号的几种不同表征（每一层代表一种表征），这些表征就是特征。自动编码器就是一种尽可能复现输入信号的神经网络。为了实现这种复现，自编码器就必须捕捉可以代表输入数据的最重要的因素，就像PCA(主成分分析)那样，找到可以代表原信息的主要成分。

1.2.1.1 网络结构

​ 堆叠自编码器的网络结构本质上就是一种普通的多层神经网络结构。

!

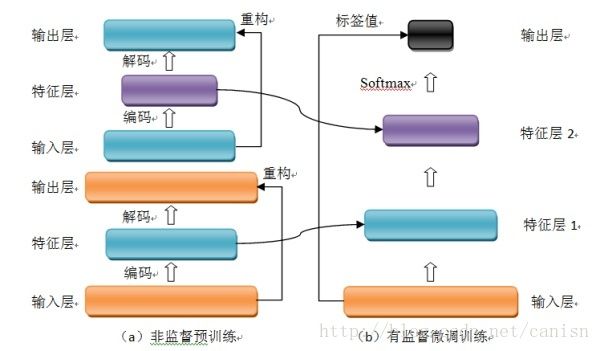
图 自编码网络结构

1.2.1.2 训练过程

​ 堆叠自编码器与普通神经网络不同之处在于其训练过程，该网络结构训练主要分两步：非监督预训练和有监督微调训练。

（1）非监督预训练

​ 自编码器通过自学习得到原始数据的压缩和分布式表征，一般用于高层特征提取与数据非线性降维。结构上类似于一个典型的三层BP神经网络，由一个输入层，一个中间隐含层和一个输出层构成。但是，输出层与输入层的神经元个数相等，且训练样本集合的标签值为输入值，即无标签值。输入层到隐含层之间的映射称为编码（Encoder），隐含层到输出层之间的映射称为解码（Decoder）。非监督预训练自编码器的中间层为特征层，在训练好第一层特征层后，第二层和第一层的训练方式相同。我们将第一层输出的特征层当成第二层的输入层，同样最小化重构误差，就会得到第二层的参数，并且得到第二层输入的特征层，也就是原输入信息的第二个表征。以此类推可以训练其他特征层。

（3）有监督微调训练

​ 经过上面的训练方法，可以得到一个多层的堆叠自编码器，每一层都会得到原始输入的不同的表达。到这里，这个堆叠自编码器还不能用来分类数据，因为它还没有学习如何去连结一个输入和一个类。它只是学习获得了一个可以良好代表输入的特征，这个特征可以最大程度上代表原输入信号。那么，为了实现分类，我们就可以在AutoEncoder的最顶的编码层添加一个分类器（例如逻辑斯蒂回归、SVM等），然后通过标准的多层神经网络的监督训练方法（梯度下降法）微调训练。

1.2.1.3 典型改进

（1）Sparse AutoEncoder稀疏自编码器

​ 在AutoEncoder的基础上加上L1的稀疏限制（L1主要是约束每一层中的节点中大部分都要为0，只有少数不为0，这就是Sparse名字的来源）来减小过拟合的影响，我们就可以得到稀疏自编码器。

（2）Denoising AutoEncoders降噪自编码器

​ 降噪自动编码器是在自动编码器的基础上，训练数据加入噪声，所以自动编码器必须学习去去除这种噪声而获得真正的没有被噪声污染过的输入。因此，这就迫使编码器去学习输入信号的更加鲁棒的表达，这也是它的泛化能力比一般编码器强的原因。

1.2.1.4 模型优缺点

(1)优点：

（1）可以利用足够多的无标签数据进行模型预训练；

（2）具有较强的数据表征能力。

(2)缺点：

（1）因为是全连接网络，需要训练的参数较多，容易出现过拟合；深度模型容易出现梯度消散问题。

（2）要求输入数据具有平移不变性。

1.2.2、Deep belief network 深度信念网络

​ 2006年，Geoffrey Hinton提出深度信念网络（DBN）及其高效的学习算法，即Pre-training+Fine tuning，并发表于《Science》上，成为其后深度学习算法的主要框架。DBN是一种生成模型，通过训练其神经元间的权重，我们可以让整个神经网络按照最大概率来生成训练数据。所以，我们不仅可以使用DBN识别特征、分类数据，还可以用它来生成数据。

1.2.2.1 网络结构

​ 深度信念网络（DBN）由若干层受限玻尔兹曼机（RBM）堆叠而成，上一层RBM的隐层作为下一层RBM的可见层。下面先介绍RBM，再介绍DBN。

（1） RBM

图2 RBM网络结构

​ 一个普通的RBM网络结构如上图所示，是一个双层模型，由m个可见层单元及n个隐层单元组成，其中，层内神经元无连接，层间神经元全连接，也就是说：在给定可见层状态时，隐层的激活状态条件独立，反之，当给定隐层状态时，可见层的激活状态条件独立。这保证了层内神经元之间的条件独立性，降低概率分布计算及训练的复杂度。RBM可以被视为一个无向图模型，可见层神经元与隐层神经元之间的连接权重是双向的，即可见层到隐层的连接权重为W，则隐层到可见层的连接权重为W’。除以上提及的参数外，RBM的参数还包括可见层偏置b及隐层偏置c。

​ RBM可见层和隐层单元所定义的分布可根据实际需要更换，包括：Binary单元、Gaussian单元、Rectified Linear单元等，这些不同单元的主要区别在于其激活函数不同。

（2） DBN

图3 DBN模型结构

​ DBN模型由若干层RBM堆叠而成，如果在训练集中有标签数据，那么最后一层RBM的可见层中既包含前一层RBM的隐层单元，也包含标签层单元。假设顶层RBM的可见层有500个神经元，训练数据的分类一共分成了10类，那么顶层RBM的可见层有510个显性神经元，对每一训练数据，相应的标签神经元被打开设为1，而其他的则被关闭设为0。

1.2.2.2 训练过程

​ DBN的训练包括Pre-training和Fine tuning两步，其中Pre-training过程相当于逐层训练每一个RBM，经过Pre-training的DBN已经可用于模拟训练数据，而为了进一步提高网络的判别性能， Fine tuning过程利用标签数据通过BP算法对网络参数进行微调。

（1） Pre-training

​ 如前面所说，DBN的Pre-training过程相当于逐层训练每一个RBM，因此进行Pre-training时直接使用RBM的训练算法。

（2） Fine tuning

​ 建立一个与DBN相同层数的神经网络，将Pre-training过程获得的网络参数赋给此神经网络，作为其参数的初始值，然后在最后一层后添加标签层，结合训练数据标签，利用BP算法微调整个网络参数，完成Fine tuning过程。

1.2.2.3 改进模型

​ DBN的变体比较多，它的改进主要集中于其组成“零件”RBM的改进，下面列举两种主要的变体。（这边的改进模型暂时没有深入研究，所以大概参考网上的内容）

（1） 卷积DBN（CDBN）

​ DBN并没有考虑到图像的二维结构信息，因为输入是简单的将一个图像矩阵转换为一维向量。而CDBN利用邻域像素的空域关系，通过一个称为卷积RBM（CRBM）的模型达到生成模型的变换不变性，而且可以容易得变换到高维图像。

（2） 条件RBM（Conditional RBM）

​ DBN并没有明确地处理对观察变量的时间联系的学习上，Conditional RBM通过考虑前一时刻的可见层单元变量作为附加的条件输入，以模拟序列数据，这种变体在语音信号处理领域应用较多。

1.2.2.4 典型优缺点

​ 对DBN优缺点的总结主要集中在生成模型与判别模型的优缺点总结上。

(1)优点：

（1）生成模型学习联合概率密度分布，所以就可以从统计的角度表示数据的分布情况，能够反映同类数据本身的相似度；

（2）生成模型可以还原出条件概率分布，此时相当于判别模型，而判别模型无法得到联合分布，所以不能当成生成模型使用。

(2)缺点：

（1） 生成模型不关心不同类别之间的最优分类面到底在哪儿，所以用于分类问题时，分类精度可能没有判别模型高；

（2）由于生成模型学习的是数据的联合分布，因此在某种程度上学习问题的复杂性更高。

（3）要求输入数据具有平移不变性。

1.3 深度置信网络相关算法

1.3.1 涉及到的相关知识

1.3.1.1 sigmoid函数

​ 神经网络最常用的激活函数之一：

sigmoid(x)=11+e−x

1.3.1.2 Bayes定理

​ 记P(A),P(B)分别表示事件A和事件B发生的概率，P(A|B)表示时间B发生的情况下A发生的概率，P（A，B）表示事件A,B同时发生的概率。则有：

P(A|B)=P(A,B)P(B),

P(A|B)=P(A)P(B|A)P(B)

​ 上式中，P(A)称为先验概率，P(A|B)称为后验概率。

1.3.1.3 二分图

​ 二分图又称二部图、双分图或偶图，是图论中的一种特殊模型。设 G=(V,E) 是一个无向图，如果顶点 V 可分割为两个互不相交的子集 V1 和 V2 ，并且图中的每条边 (i,j) 所关联的两个顶点分别属于两个不同的顶点集，即 i∈V1,j∈V2 ，或者 i∈V2,j∈V1 ，则称图 G 是一个二分图

1.3.1.4 MCMC方法（蒙特卡罗方法）

​ 求一个已知分布的函数的积分 ∫bah(x)dx ，如果无法获得解析解，可以将函数分解为某个函数和一个定义在 (a,b) 区间上的密度函数 p(x) 的乘积，这样整个积分即可以写成

intbah(x)dx=∫baf(x)p(x)dx=Ep(x)[f(x)]

这样原积分机就等于 f(x) 在 p(x) 这个分布上的均值。从该分布上采集大量的样本点 x1,x2,x3… ，这些分布符合分布 p(x) ，即对任意 i ，

xi∑ni=1xi≈p(xi) ，

​ 那么我们就可以通过这些采样来逼近这个均值

∫bah(x)d(x)=Ep(x)[f(x)]≈1n∑ni=1f(xi)

​ 问题是如何采集该分布下的无偏估计，于是就有了马尔可夫链蒙特卡罗方法（Markov chain Monte Carlo, MCMC）方法。基本思想就是利用马尔科夫链来产生指定分布下的样本。

1.3.1.5 马尔可夫链

​ 设 Xt 表示随机变量 X 在离散事件 t 时刻的取值，若该变量随时间变化的转移概率仅仅依赖于它的当前取值，即：

P(Xt+1=sj|X0=si0,X1=si1,⋯,Xt=st)=P(Xt+1=sj|Xt=si)

​ 则这个变量称为马尔科夫变量，其中 si0si1,⋯,si,sj∈Ω 为随机变量 X 可能的状态，这个性质称为马尔科夫性质，具有马尔科夫性质的随机过程称为马尔科夫过程。

​ 设状态数目为n，则有

(πt+11,…,πt+1n)=(πt1,…,πtn)⎡⎣⎢⎢⎢⎢P1,1P2,1Pn,1P1,2P2,2Pn,2…………P1,nP2,nPn,n⎤⎦⎥⎥⎥⎥

​ 如果马尔科夫链中的某个取值在n次转移后会回到自身，那么这个过程具有周期性，如果任意两个取值之间都可以以非零概率互相转移，则过程称为不可约，如果一个过程不是周期性的，也不是不可约的，那就是各态遍历的，这样的过程在一定数量的转移步骤后，一定会收敛于唯一一个平稳分布 π∗ ，即：

limt→∞π0Pt=π∗

​ 且这个分布有：

π∗P=π∗

​ 也就是说，如果分布式各态遍历的，通过模拟平稳分布的马尔科夫链过程，在经过足够多次数的转移后就可以采集到目标分布下的样本。

1.3.1.6 正则分布

​ 统计力学的一个基本结论是：但系统与外界达到热平衡时，系统处于状态 i 的概率 pi 具有以下形式：

pi=1ZTe−EiT

​ 其中，

ZT=∑ie−EiT

称为归一化常数， T 为正数，表示系统所处的温度，这种概率分布的形式叫做正则分布。

1.3.1.7 Metropolis-Hastings采样

​ M-H采样是一种非常重要的MCMC采样算法，并且对于状态转移过程建立了统一的框架。M-H采样算法中，要采集分布 π(.) 上的样本，引入一个转移提议分布 Q(.;i) ，这个分布的作用是，根据我们的当前状态 i ，提议转移之后的状态，每次转移时，我们首先利用 Q(.;i) 提议下一步的状态，然后以下面的概率接受这个状态，接受概率为：

α(i→j)=min{1,π(j)Q(i;j)π(i)Q(j;i)}

​ 由上式推到可得到：

π(i)P(i→j)======π(i)α(i→j)Q(j;i)π(i)min{1,π(j)Q(i;j)π(i)Q(j;i)}Q(j;i)min{π(i)Q(j;i),π(j)Q(i;j)}π(j)min{1,π(i)Q(j;i)π(j)Q(i;j)}Q(i;j)π(j)α(i→i)Q(i;j)π(j)P(j→i)

​ 即满足细致平稳条件，这样转移概率就是：

P(i→j)=α(i→j)Q(j;i)

​ 其中 α(i→j) 先跟一个 (0,1) 随机数比较来选择是否接受。 Q(j;i) 表示从 i 到 j 的转移概率， Q(.;.) 可以选择一些简单的分布。

1.3.1.8 Gibbs采样

​ Gibbs采样时M-H采样的特殊形式。Gibbs采样没有了接受概率，保证了过程的收敛速度。算法流程如下：

1. 初始化系统状态为 X(0) .

2. 初始化时间 t←0 .

3. 对每个变量 xi,i∈1,2,…,m ,按以下条件概率对其采样

   ​ P(xt+1i|xt+11,…,xt+1i−1,xti+1,…,xtm)

4. t←t+1 .

5. 若 t 少于足够的转移次数，则返回第3步.

6. 返回 X(t) 作为采集到的样本。

1.3.2 受限玻尔兹曼机（RBM）网络结构

​ 深度信念网络（DBN）由若干层受限玻尔兹曼机（RBM）堆叠而成，上一层RBM的隐层作为下一层RBM的可见层。下面先介绍RBM，再介绍DBN。

（1） RBM

图 RBM网络结构

​ 一个普通的RBM网络结构如上图所示，是一个双层模型，由m个可见层单元及n个隐层单元组成，其中，层内神经元无连接，层间神经元全连接，也就是说：在给定可见层状态时，隐层的激活状态条件独立，反之，当给定隐层状态时，可见层的激活状态条件独立。这保证了层内神经元之间的条件独立性，降低概率分布计算及训练的复杂度。RBM可以被视为一个无向图模型，可见层神经元与隐层神经元之间的连接权重是双向的，即可见层到隐层的连接权重为W，则隐层到可见层的连接权重为W’。除以上提及的参数外，RBM的参数还包括可见层偏置b及隐层偏置c。

​ RBM可见层和隐层单元所定义的分布可根据实际需要更换，包括：Binary单元、Gaussian单元、Rectified Linear单元等，这些不同单元的主要区别在于其激活函数不同。

1.3.3 能量函数和概率分布

​ RBM是一个基于能量的魔性，对于状态 (v,h) ，可定义如下能量函数：

Eθ(v,h)=−∑nvi=1aivi−∑nhj=1bjhj−∑nvi=1∑nhj=1hjwj,ivi

​ 写成向量形式为：

Eθ(v,h)=−aTv−bTh−hTWv

​ 利用能量函数定义可以得到 (v,h) 的联合概率分布

Pθ(v,h)=1Zθe−Eθ(v,h) ,

​ 其中，

Zθ=∑v,he−Eθ(v,h)

​ 对于一个实际问题，我们关心的是观测数据 v 的概率分布 Pθ(v,h) 的边缘分布，也称为似然函数，具体为：

Pθ(v)=∑hPθ(v,h)=1Zθ∑he−Eθ(v,h) ,

​ 同样地，有：

Pθ(h)=∑vPθ(h,v)=1Zθ∑ve−Eθ(v,h) .

1.3.4对数似然函数

​ 给定训练样本后，训练一个RBM意味着调整参数 θ ，以拟合给定的训练样本，即，使得在该参数下由相应RBM表示的概率分布尽可能地与训练数据相符合。假定集合为：

S={v1,v2,…,vns} ,

​ 其中 ns 为训练样本的数目， vi=(vi1,vi2,…,vinv,)T,i=1,2,…,ns ，他们是独立同分布的，训练RBM的目标就是最大化如下似然：

Lθ,s=∏nsi=1P(vi)

​ 由于连乘不好处理，根据 lns 函数单调性可得：

lnLθ,s=ln∏nsi=1P(vi)=∑nsi=1lnP(vi)

​ 以下记 lnLθ,s 为 lnLs 。

1.3.5 梯度计算

1.3.6 对比散度算法

​ 尽管利用Gibbs采样，我们可以得到对数似然函数关于未知参数梯度的近似，但是通常情况下，需要使用较大的采样步数，这使得RBM的训练效率仍然不高，尤其当观测数据的特征维数较高时。2002年Hinton提出了RBM的一个快速学习算法，对比散度算法(Contrastive Divergence)。与Gibbs采样不同，Hinton指出，当使用训练数据初始化 v0 时，我们仅需要使用k（通常k＝1）步Gibbs采样就可以得到足够好的近似。在CD算法一开始，可见单元的状态被设置成一个训练样本，并利用以下公式计算隐藏层单元的二值状态，在所有隐藏单元状态确定了之后，根据下面公式2来确定每个可见单元取值为1的概率。进而得到可见层的一个重构。然后将重构的可见层作为真实的模型带入RBM的 Δ 中，就可以进行梯度下降算法了。

1.3.7 RBM训练算法

1.3.8 RBM评估

1.4 深度信念网络的tensorflow实现例程

• import tensorflow as tf
  import numpy as np
  from tensorflow.examples.tutorials.mnist import input_data
  from PIL import Image
  
  def sample_prob(probs):
    return tf.nn.relu(tf.sign(
        probs - tf.random_uniform(tf.shape(probs))))
  
  def scale_to_unit_interval(ndar, eps=1e-8):
    """ Scales all values in the ndarray ndar to be between 0 and 1 """
    ndar = ndar.copy()
    ndar -= ndar.min()
    ndar *= 1.0 / (ndar.max() + eps)
    return ndar
  
  def tile_raster_images(X, img_shape, tile_shape, tile_spacing=(0, 0),
                       scale_rows_to_unit_interval=True,
                       output_pixel_vals=True):
    """
    Transform an array with one flattened image per row, into an array in
    which images are reshaped and layed out like tiles on a floor.
    This function is useful for visualizing datasets whose rows are images,
    and also columns of matrices for transforming those rows
    (such as the first layer of a neural net).
    :type X: a 2-D ndarray or a tuple of 4 channels, elements of which can
    be 2-D ndarrays or None;
    :param X: a 2-D array in which every row is a flattened image.
    :type img_shape: tuple; (height, width)
    :param img_shape: the original shape of each image
    :type tile_shape: tuple; (rows, cols)
    :param tile_shape: the number of images to tile (rows, cols)
    :param output_pixel_vals: if output should be pixel values (i.e. int8
    values) or floats
    :param scale_rows_to_unit_interval: if the values need to be scaled before
    being plotted to [0,1] or not
    :returns: array suitable for viewing as an image.
    (See:`Image.fromarray`.)
    :rtype: a 2-d array with same dtype as X.
    """
    assert len(img_shape) == 2
    assert len(tile_shape) == 2
    assert len(tile_spacing) == 2
    # The expression below can be re-written in a more C style as
    # follows :
    #
    # out_shape    = [0,0]
    # out_shape[0] = (img_shape[0]+tile_spacing[0])*tile_shape[0] -
    #                tile_spacing[0]
    # out_shape[1] = (img_shape[1]+tile_spacing[1])*tile_shape[1] -
    #                tile_spacing[1]
    out_shape = [
        (ishp + tsp) * tshp - tsp
        for ishp, tshp, tsp in zip(img_shape, tile_shape, tile_spacing)
    ]
  
    if isinstance(X, tuple):
        assert len(X) == 4
        # Create an output numpy ndarray to store the image
        if output_pixel_vals:
            out_array = np.zeros(
                (out_shape[0], out_shape[1], 4), dtype='uint8')
        else:
            out_array = np.zeros(
                (out_shape[0], out_shape[1], 4), dtype=X.dtype)
  
        # colors default to 0, alpha defaults to 1 (opaque)
        if output_pixel_vals:
            channel_defaults = [0, 0, 0, 255]
        else:
            channel_defaults = [0., 0., 0., 1.]
  
        for i in range(4):
            if X[i] is None:
                # if channel is None, fill it with zeros of the correct
                # dtype
                dt = out_array.dtype
                if output_pixel_vals:
                    dt = 'uint8'
                out_array[:, :, i] = np.zeros(
                    out_shape,
                    dtype=dt
                ) + channel_defaults[i]
            else:
                # use a recurrent call to compute the channel and store it
                # in the output
                out_array[:, :, i] = tile_raster_images(
                    X[i], img_shape, tile_shape, tile_spacing,
                    scale_rows_to_unit_interval, output_pixel_vals)
        return out_array
    else:
        # if we are dealing with only one channel
        H, W = img_shape
        Hs, Ws = tile_spacing
  
        # generate a matrix to store the output
        dt = X.dtype
        if output_pixel_vals:
            dt = 'uint8'
        out_array = np.zeros(out_shape, dtype=dt)
  
        for tile_row in range(tile_shape[0]):
            for tile_col in range(tile_shape[1]):
                if tile_row * tile_shape[1] + tile_col < X.shape[0]:
                    this_x = X[tile_row * tile_shape[1] + tile_col]
                    if scale_rows_to_unit_interval:
                        # if we should scale values to be between 0 and 1
                        # do this by calling the `scale_to_unit_interval`
                        # function
                        this_img = scale_to_unit_interval(
                            this_x.reshape(img_shape))
                    else:
                        this_img = this_x.reshape(img_shape)
                    # add the slice to the corresponding position in the
                    # output array
                    c = 1
                    if output_pixel_vals:
                        c = 255
                    out_array[
                        tile_row * (H + Hs): tile_row * (H + Hs) + H,
                        tile_col * (W + Ws): tile_col * (W + Ws) + W
                    ] = this_img * c
        return out_array
  
  if __name__ == '__main__':
    alpha = 1.0
    batchsize = 100
  
    mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
    trX, trY, teX, teY = mnist.train.images, mnist.train.labels,\
        mnist.test.images, mnist.test.labels
  
    X = tf.placeholder("float", [None, 784])
    Y = tf.placeholder("float", [None, 10])
  
    rbm_w = tf.placeholder("float", [784, 500])
    rbm_vb = tf.placeholder("float", [784])
    rbm_hb = tf.placeholder("float", [500])
    h0 = sample_prob(tf.nn.sigmoid(tf.matmul(X, rbm_w) + rbm_hb))
    v1 = sample_prob(tf.nn.sigmoid(
        tf.matmul(h0, tf.transpose(rbm_w)) + rbm_vb))
    h1 = tf.nn.sigmoid(tf.matmul(v1, rbm_w) + rbm_hb)
    w_positive_grad = tf.matmul(tf.transpose(X), h0)
    w_negative_grad = tf.matmul(tf.transpose(v1), h1)
    update_w = rbm_w + alpha * \
        (w_positive_grad - w_negative_grad) / tf.to_float(tf.shape(X)[0])
    update_vb = rbm_vb + alpha * tf.reduce_mean(X - v1, 0)
    update_hb = rbm_hb + alpha * tf.reduce_mean(h0 - h1, 0)
  
    h_sample = sample_prob(tf.nn.sigmoid(tf.matmul(X, rbm_w) + rbm_hb))
    v_sample = sample_prob(tf.nn.sigmoid(
        tf.matmul(h_sample, tf.transpose(rbm_w)) + rbm_vb))
    err = X - v_sample
    err_sum = tf.reduce_mean(err * err)
  
    sess = tf.Session()
    init = tf.initialize_all_variables()
    sess.run(init)
  
    n_w = np.zeros([784, 500], np.float32)
    n_vb = np.zeros([784], np.float32)
    n_hb = np.zeros([500], np.float32)
    o_w = np.zeros([784, 500], np.float32)
    o_vb = np.zeros([784], np.float32)
    o_hb = np.zeros([500], np.float32)
    print(sess.run(
        err_sum, feed_dict={X: trX, rbm_w: o_w, rbm_vb: o_vb, rbm_hb: o_hb}))
  
    for start, end in zip(range(0, len(trX), batchsize),
                          range(batchsize, len(trX), batchsize)):
        batch = trX[start:end]
        n_w = sess.run(update_w, feed_dict={
                       X: batch, rbm_w: o_w, rbm_vb: o_vb, rbm_hb: o_hb})
        n_vb = sess.run(update_vb, feed_dict={
                        X: batch, rbm_w: o_w, rbm_vb: o_vb, rbm_hb: o_hb})
        n_hb = sess.run(update_hb, feed_dict={
                        X: batch, rbm_w: o_w, rbm_vb: o_vb, rbm_hb: o_hb})
        o_w = n_w
        o_vb = n_vb
        o_hb = n_hb
        if start % 10000 == 0:
            print(sess.run(err_sum, feed_dict={
                  X: trX, rbm_w: n_w, rbm_vb: n_vb, rbm_hb: n_hb}))
            image = Image.fromarray(
                tile_raster_images(
                    X=n_w.T,
                    img_shape=(28, 28),
                    tile_shape=(25, 20),
                    tile_spacing=(1, 1)
                )
            )
            image.save("save/rbm_%d.png" % (start / 10000))

2. 卷积神经网路CNN

3. 递归神经网络RNN

4. 忆阻神经网络

4.1 前言

​ 人工神经网络模拟人脑，复杂度高，系统极其复杂。忆阻器出现使得人工神经网络可以更加复杂。

4.2 忆阻器

​ 忆阻器表示磁通和点和电荷之间的关系。忆阻器可以通过外界电压电流的改变来改变自身电阻并保持的一种元件 。

4.3参考文献

1. 忆阻器在神经网络中的应用研究