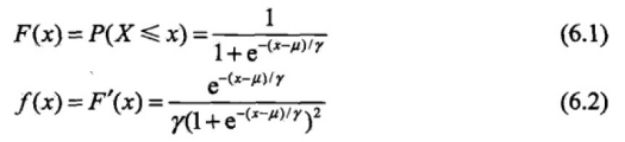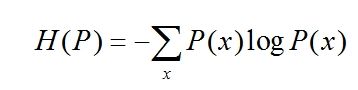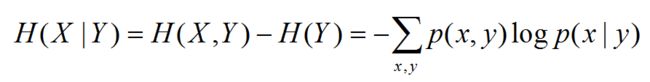《统计学习方法》笔记(五)逻辑斯蒂回归与最大熵模型
LR回归(Logistic Regression)
LR回归,虽然这个算法从名字上来看,是回归算法,但其实际上是一个分类算法。在机器学习算法中,有几十种分类器,LR回归是其中最常用的一个。
LR回归是在线性回归模型的基础上,使用sigmoid函数,将线性模型$w_T$x的结果压缩到[0,1]之间,使其拥有概率意义。其本质仍然是一个线性模型,实现相对简单。在广告计算和推荐系统中使用频率极高,是CTR预估模型的基本算法。同时,LR模型也是深度学习的基本组成单元。
LR回归属于概率性判别式模型,之所谓是概率性模型,是因为LR模型是有概率意义的;之所以是判别式模型,是因为LR回归并没有对数据的分布进行建模,也就是说,LR模型并不知道数据的具体分布,而是直接将判别函数,或者说是分类超平面求解了出来。
逻辑斯谛分布
设X是连续随机变量,X服从逻辑斯谛分布是指X服从如下分布函数和密度函数:
其中,为位置参数,> 0 为形状参数。
密度函数f(x)和分布函数F(x)的图形如图所示:
分布函数属于逻辑斯谛函数,其图形是一条S形曲线,该曲线以点(μ,½)为中心对称,即满足;
曲线在中心附近增长速度较快,在两端增长速度较慢,形状参数γ的值越小,曲线在中心附近增长的越快。
Logistic Regression回归是感知机和神经网络模型的组成基础,所以我们可以以神经网络的角度来看待它。将一个Logistic Regression回归看成一个神经元,其参数的训练看成神经元的参数训练,只不过它不含隐藏层而已。本例中的模型可以看成:
最大熵模型
在满足约束条件的模型集合中选取熵最大的模型。最大熵原理认为要选择的概率模型首先必须满足已有的事实,即约束条件。在没有更多信息的情况下,那些不确定的部分都是“等可能的”。
基本概念
熵是随机变量不确定性的度量,不确定性越大,熵值就越大;若随机变量退化成定值,熵为0。均匀分布是“最不确定”的分布
假设离散随机变量X的概率分布为P(x),则其熵为:
联合熵和条件熵
两个随机变量的X,Y的联合分布,可以形成联合熵,用H(X,Y)表示
条件熵H(X|Y) = H(X,Y) - H(Y)
相对熵与互信息
设p(x),q(x)是X中取值的两个概率分布,则p对q的相对熵是:
两个随机变量X,Y的互信息,定义为X,Y的联合分布和独立分布乘积的相对熵。
最大熵模型写成更一般的形式.
最大熵模型的学习最终可以归结为以最大熵模型似然函数为目标函数的优化问题。这时的目标函数是凸函数,因此有很多种方法都能保证找到全局最优解,例如改进的迭代尺度法(IIS),梯度下降法,牛顿法或拟牛顿法,牛顿法或拟牛顿法一般收敛比较快。
最大熵模型小结
最大熵模型在分类方法里算是比较优的模型,但是由于它的约束函数的数目一般来说会随着样本量的增大而增大,导致样本量很大的时候,对偶函数优化求解的迭代过程非常慢,scikit-learn甚至都没有最大熵模型对应的类库。但是理解它仍然很有意义,尤其是它和很多分类方法都有千丝万缕的联系。
我们总结下最大熵模型作为分类方法的优缺点:
最大熵模型的优点有:
a) 最大熵统计模型获得的是所有满足约束条件的模型中信息熵极大的模型,作为经典的分类模型时准确率较高。
b) 可以灵活地设置约束条件,通过约束条件的多少可以调节模型对未知数据的适应度和对已知数据的拟合程度
最大熵模型的缺点有:
a) 由于约束函数数量和样本数目有关系,导致迭代过程计算量巨大,实际应用比较难。