【模板】单纯形法
文章目录
- 线性规划
- 标准型
- 松弛型
- 网络流模型
- 单纯形
- 单纯形法
- 代码
- 参考资料
线性规划
线性规划问题要求最大化或最小化一个受限于一组有限的线性约束的线性函数。
具体表现为:
已知一组实数 a 1 , a 2 , . . , a n a_1,a_2,..,a_n a1,a2,..,an,以及一组变量 x 1 , x 2 , . . , x n x_1,x_2,..,x_n x1,x2,..,xn,设在这些变量上的一个线性函数为
f ( x 1 , x 2 , . . , x n ) = ∑ i = 1 n a i x i f(x_1,x_2,..,x_n)=\sum\limits_{i=1}^na_ix_i f(x1,x2,..,xn)=i=1∑naixi。
给定 b b b, f ( x 1 , x 2 , . . , x n ) ≤ b , = b f(x_1,x_2,..,x_n)\leq b,=b f(x1,x2,..,xn)≤b,=b或 ≥ b \geq b ≥b统称为线性约束。
称满足所有限制条件的解 x 1 , x 2 , . . , x n x_1,x_2,..,x_n x1,x2,..,xn为可行解,使目标函数达到最优的可行解为最优解,所有可行解构成的区域为解空间。
标准型
最大化 ∑ i = 1 n c i x i \quad\quad \quad \quad \quad \quad \quad\quad\quad\sum\limits_{i=1}^nc_ix_i i=1∑ncixi
满足约束 ∑ j = 1 n a i , j x j ≤ b i i = 1 , 2 , . . , m \quad\quad\quad\sum\limits_{j=1}^na_{i,j}x_j\leq b_i\quad i=1,2,..,m j=1∑nai,jxj≤bii=1,2,..,m
x j ≥ 0 j = 1 , 2 , . . , n \quad\quad\quad \quad \quad \quad \quad \quad \quad \ \ x_j\geq0 \quad j=1,2,..,n xj≥0j=1,2,..,n
所有的线性规划问题经过变换后都可以用标准型来表示。
松弛型
最大化 ∑ i = 1 n c i x i \quad \quad \quad \quad \quad \quad \quad\quad\quad\sum\limits_{i=1}^nc_ix_i i=1∑ncixi
满足约束 x i + n = b i − ∑ j = 1 n a i , j x j i = 1 , 2 , . . , m \quad\quad\quad x_{i+n}=b_i-\sum\limits_{j=1}^na_{i,j}x_j\quad i=1,2,..,m xi+n=bi−j=1∑nai,jxji=1,2,..,m
x j ≥ 0 j = 1 , 2 , . . , n \quad\quad\quad \quad \quad \quad \quad \quad \quad \ \ x_j\geq0 \quad j=1,2,..,n xj≥0j=1,2,..,n
网络流模型
设 f ( u , v ) f(u,v) f(u,v)表示 ( u , v ) (u,v) (u,v)的流量, c ( u , v ) c(u,v) c(u,v)表示流量上界, w ( u , v ) w(u,v) w(u,v)表示费用。
最大流:
从汇点 t t t向 s s s连容量为 + ∞ +\infty +∞的边,满足流量守恒之后,求最大流量。
最大化 f ( s , t ) \quad \quad \quad \quad \quad \quad \quad\quad\quad f(s,t) f(s,t)
满足约束 f ( u , v ) ≤ c ( u , v ) ( u , v ) ∈ E \quad\quad\quad \quad \quad \quad f(u,v)\leq c(u,v) \quad \quad \quad (u,v)\in E f(u,v)≤c(u,v)(u,v)∈E
∑ u f ( u , v ) = ∑ u f ( v , u ) v ∈ V \quad\quad\quad \quad \quad \quad \quad \quad \ \sum\limits_{u}f(u,v)=\sum\limits_{u}f(v,u) \quad \quad v\in V u∑f(u,v)=u∑f(v,u)v∈V
f ( u , v ) ≥ 0 ( u , v ) ∈ E ∪ { ( t , s ) } \quad\quad\quad \quad \quad \quad \quad \quad \quad \quad \ f(u,v)\geq 0 \quad \quad(u,v)\in E\cup\{(t,s)\} f(u,v)≥0(u,v)∈E∪{(t,s)}
最小费用流:
从汇点 t t t向 s s s连容量为 + ∞ +\infty +∞,费用为 0 0 0的边,满足流量守恒之后,求最小费用流。
最小化 ∑ ( u , v ) ∈ E w ( u , v ) f ( u , v ) \quad \quad \quad \quad \quad \quad \quad\quad\quad \sum\limits_{(u,v)\in E} w(u,v)f(u,v) (u,v)∈E∑w(u,v)f(u,v)
满足约束 f ( u , v ) ≤ c ( u , v ) ( u , v ) ∈ E \quad\quad\quad \quad \quad \quad f(u,v)\leq c(u,v) \quad \quad \quad (u,v)\in E f(u,v)≤c(u,v)(u,v)∈E
∑ u f ( u , v ) = ∑ u f ( v , u ) v ∈ V \quad\quad\quad \quad \quad \quad \quad \quad \ \sum\limits_{u}f(u,v)=\sum\limits_{u}f(v,u) \quad \quad v\in V u∑f(u,v)=u∑f(v,u)v∈V
f ( u , v ) ≥ 0 ( u , v ) ∈ E ∪ { ( t , s ) } \quad\quad\quad \quad \quad \quad \quad \quad \quad \quad \ f(u,v)\geq 0 \quad \quad(u,v)\in E\cup\{(t,s)\} f(u,v)≥0(u,v)∈E∪{(t,s)}
最小费用最大流:
加上一个约束条件 f ( t , s ) = m a x f l o w f(t,s)=maxflow f(t,s)=maxflow即可。
单纯形
单纯形是指 k k k维空间中有 k + 1 k+1 k+1个顶点的凸多面体(如三角形,四面体)。
一个线性规划的解空间是所有线性不等式解空间的交。而注意到对于每个线性不等式的解空间都是一个凸形区域(定义:区域内任意两点连线上的点都属于这个区域),可以归纳证明,线性规划的解空间是一个凸形区域。
不考虑最优解无穷大/小的情况,在一个凸形区域上,它的所有局部最优解必然只有一个值(且等于全局最优解的值)。可以类似于爬山算法,贪心向全局最优解趋近。
在这个凸多边形上求解最优值的一个一般性方法就称为单纯形法。
单纯形法
等式问题比较好解决,所以单纯形法求解线性规划时先将其转化为松弛型:
最大化 ∑ i = 1 n c i x i \quad \quad \quad \quad \quad \quad \quad\quad\quad\sum\limits_{i=1}^nc_ix_i i=1∑ncixi
满足约束 x i + n = b i − ∑ j = 1 n a i , j x j i = 1 , 2 , . . , m \quad\quad\quad x_{i+n}=b_i-\sum\limits_{j=1}^na_{i,j}x_j\quad i=1,2,..,m xi+n=bi−j=1∑nai,jxji=1,2,..,m
x j ≥ 0 j = 1 , 2 , . . , n \quad\quad\quad \quad \quad \quad \quad \quad \quad \ \ x_j\geq0 \quad j=1,2,..,n xj≥0j=1,2,..,n
其中 x 1 , x 2 , . . , x n x_1,x_2,..,x_n x1,x2,..,xn这些在等式右边的变量称为非基变量, x n + 1 , x n + 2 , . . , x n + n x_{n+1},x_{n+2},..,x_{n+n} xn+1,xn+2,..,xn+n这些在等式左边的变量称为基变量。
当所有 b i ≥ 0 b_i\geq0 bi≥0时,所有基变量等于 b i b_i bi,非基变量等于0就是一组可行解,这样的解称为基本解。单纯形算法中只需要考虑基本解。
基本操作
下面介绍一个单纯形一个重要操作:转轴(pivot)。
p i v o t ( b , n ) pivot(b,n) pivot(b,n)指将基变量 x B x_B xB与非基变量 x N x_N xN互换(称这个 x N x_N xN为换入变量, x B x_B xB为换出变量)。具体而言是将 x N x_N xN放在原本 x B x_B xB所在的等式左侧,而用 x B x_B xB和其他非基变量来替代 x N x_N xN。
由 x B = b i − ∑ j = 1 n a i , j x j x_B=b_i-\sum\limits_{j=1}^na_{i,j}x_j xB=bi−j=1∑nai,jxj
得到 x N = b i − ∑ j = 1 , j ≠ N n a i , j x j − x B a i , N x_N=\dfrac{b_i-\sum\limits_{j=1,j\neq N}^na_{i,j}x_j-x_B}{a_{i,N}} xN=ai,Nbi−j=1,j̸=N∑nai,jxj−xB
注意转轴操作需满足: a i , N ≠ 0 a_{i,N}\neq 0 ai,N̸=0。
另一个重要操作:simplex。
具体的最优化过程如下:
- 选择一个满足 c e > 0 c_e>0 ce>0的非基变量 x e x_e xe
- 找到满足 a l , e > 0 a_{l,e}>0 al,e>0且 b l a l , e \dfrac{b_l}{a_{l,e}} al,ebl最小的基变量 x n + l x_{n+l} xn+l
- 执行pivot(l,e),然后回到第一步
首先把 x 1 x_1 x1作为换入变量,因为 c 1 > 0 c_1>0 c1>0,所以增大 x 1 x_1 x1必然使得解增大,而因为约束条件导致 x 1 x_1 x1增大必然有个上限,在第三个约束中最紧: x 1 ≤ 9 x_1\leq 9 x1≤9,把 x 6 x_6 x6作为换出变量。
取约束最近的是因为这样代换后能保证其他所有等式中 b i b_i bi仍然满足 ≥ 0 \geq 0 ≥0。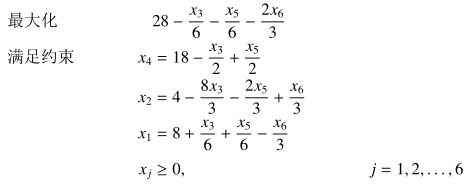
不断迭代最终得到一个 c i c_i ci都 ≤ 0 \leq 0 ≤0的式子,而 x i ≥ 0 x_i\geq 0 xi≥0导致无法得到更大的解了。
最优解就是当前的基本解。
若存在 c e > 0 c_e>0 ce>0但所有 a l , e a_{l,e} al,e都 ≤ 0 \leq 0 ≤0时,最优解可以达到正无穷。
但是基本解和上述过程都是在所有 b i ≥ 0 b_i\geq 0 bi≥0的前提下进行的,如果有 b i < 0 b_i<0 bi<0怎么办呢?
法1(论文中的方法):
若最优解中 x 0 ≠ 0 x_0\neq 0 x0̸=0,则无解。
找到最小的 b l b_l bl,把 x l + n x_{l+n} xl+n作为换出变量执行一次转轴操作(因为 b l < 0 b_l<0 bl<0且 b l b_l bl最小,所以这样代换后满足所有 b i ≥ 0 b_i\geq 0 bi≥0)。
代入第二项:

最后得到:

那么存在最优解 0 0 0。不失一般性,如果最后 x 0 x_0 x0不是基变量,再转轴操作一次即可( x 0 = 0 x_0=0 x0=0,所以 b i = 0 b_i=0 bi=0,因此选择任意转轴即可,除了 a i j ≠ 0 a_ij\neq 0 aij̸=0以外没有限制)。
然后把 x 0 x_0 x0代出,换回最初的式子(是基变量的就用其它非基变量表达)后进行 s i m p l e x simplex simplex操作即可。
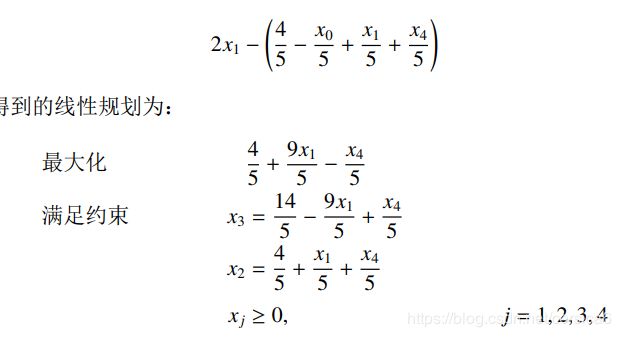
法2(uoj上学到的方法):
这个方法相较上一个方法简捷许多。
我们的目标是让所有 b i ≥ 0 b_i\geq 0 bi≥0。
所以每次选择一个 b i < 0 b_i<0 bi<0的基变量 x n + l x_{n+l} xn+l,在该约束右边找一个 a i , j < 0 a_{i,j}<0 ai,j<0(即系数为正)的非基变量 x e x_e xe,进行转轴操作即可。
若在右边所有 a i , j ≥ 0 a_{i,j}\geq 0 ai,j≥0,则无解。
复杂度分析
有一个不会证明的定理:
一般线性规划问题可以在多项式时间内解决。
1s过几百的样子。。。
一次转轴操作复杂度为 O ( n m ) O(nm) O(nm),而最优化(解决 b i < 0 b_i<0 bi<0的情况)操作中转轴操作调用次数可能为指数级,但上界很难卡满。
理论复杂度(???):
法1: O ( n 3.5 m 2 ) O(n^{3.5}m^2) O(n3.5m2)
法2: O ( n 3.5 m ) O(n^{3.5}m) O(n3.5m)
代码
实际上并不需要真的把松弛型建出来,具体看代码吧(只需要记录 x 1 , x 2 , . . , x n x_1,x_2,..,x_n x1,x2,..,xn的位置即可)。
传送门:uoj179
#include参考资料
- 2016国家集训队论文《浅谈线性规划与对偶问题》董克凡
- 单纯形法-fjzzq2002