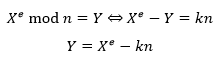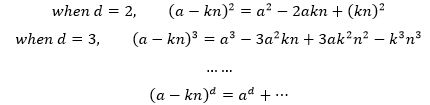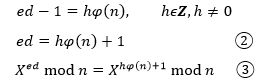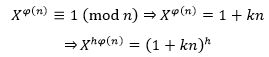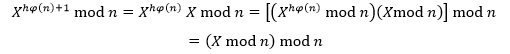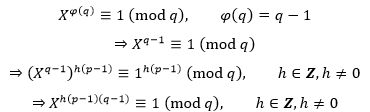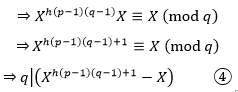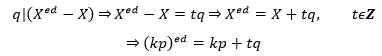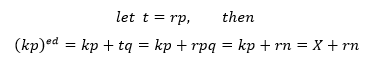上一篇文章介绍了RSA涉及的数学知识,本章将应用这些知识详解RSA的加密与解密。
RSA算法的密钥生成过程
密钥的生成是RSA算法的核心,它的密钥对生成过程如下:
1. 选择两个不相等的大素数p和q,计算出n=pq,n被称为RSA算法的公共模数;
2. 计算n的欧拉数φ(n),φ(n)=(p-1)(q-1);
3. 随机选择一个整数e作为公钥加密密钥指数,1< e < φ(n),且e与φ(n)互质;
4. 利用同余方程ed≡1 (mod φ(n))计算e对应的私钥解密指数d。由于GCD(e, φ(n))=1,因此同余方程有唯一解,d就是e对于模φ(n)的乘法逆元;
5. 将(e,n)封装成公钥,(d, n)封装成私钥,同时销毁p和q。
由于n已经被公开出去,剩下的d就成为RSA有效性的关键,如果d被破解,那么密码系统也宣告失效。至于能否破解,后续再议,先来看看RSA是的加密和解密算法。
RSA的加密和解密算法
现在Bob通过上述过程生成了公钥和私钥,并把公钥告知了Alice,如果Alice想和Bob通讯,就需要用Bob的公钥PKB对发送的明文X进行加密,从而得到密文Y:
在RSA中,Ee,n(X)是模幂运算,先计算X的e次方,再对其结果用n求余:
![]()
Bob收到密文后,需要对其解密,还原出明文X,解密运算也是模幂运算:
![]()
所有信息(包括文字、语音、图像、视频等)在计算机中都是二进制数据,因此可以将X和Y视为整数,进而使用摸幂运算。
加密运算容易理解,解密运算为什能还原出明文呢?如果a%n=b,则下面的表达是等同的:
因此加密过程在表达上等同于:
将密文代入解密运算:
![]()
继续计算似乎有点困难,不妨先把问题简化,令a=Xe:
这里有一个规律,展开式只有第一项不含有kn,这意味着(a-kn)d能否被n整除完全取决于展开式的第一项,因此:
在生成密钥的第4步,根据ed≡1 (mod φ(n))计算出了d,这意味着:
根据欧拉定理,如果a, n是正整数,且二者互质,则:
![]()
因此,当X和n互质时:
根据①可知:
![]()
根据模运算的性质:
![]()
③可进一步简化为:
这里有两种情况,X>=n或X
![]()
当X>=n是,情况变得有些微妙,假设X=37,n=35:
![]()
这下可坏了,解密算法根本无法还原出明文。难道是解密算法有误?实际上RSA的加密是有前提条件的,根据RSA规范(https://tools.ietf.org/html/rfc2437),明文的取值范围必须在0到n-1之间:
看来只能是 X
当X和n不互质时,它们必然有除了1以外的其它公约数;由于n只有p和q两个约数,因此p或q也一定是X的约数,也就是说X=kp或X=kq。假设X=kp,如果X与q不互质,q本身又是与p互质的素数,因此k一定是q的整数倍:
这里用使了同余的性质,若 a≡b mod m,则:an≡bn mod m 。
同余符号两侧同时乘以 X:
根据②:
代入④中:
因为(kp)ed能够被p整除,所以kp+tq也能被p整除,同时kp也能被p整除,根据整除的性质,tq也能被p整除;由于p和q互质,所以t一定是p的倍数:
现在可以把这个结论代入①中继续进行解密运算:
![]()
根据模运算规则:
![]()
解密运算进一步简化为:
由于RSA规范限制X
![]()
现在可以知道,在RSA规范的限制下,RSA的解密确实可以还原出明文。
假设Bob选择了两个素数,p=113,q=59,由此计算出n=6667,φ(n)=112*58=6496;之后Bob选择了一个与6496互质的小质数e=17作为密密钥指数,再使用前面介绍的扩展欧几里德算法用extEculid(17, 6496)计算出乘法逆元d=3057;最后,Bob把(17, 6667)作为公钥发送给Alice,把(3057,6667)作为私钥留给了自己。
现在,Alice向Bob发送了一个520的数字,经过加密运算后生成了密文:
![]()
Bob收到后用自己的私钥对其解密:
![]()
RSA的安全性
密码体制的安全性依赖于密钥的安全性,现代密码学不追求加密算法的保密性,而是追求加密算法的完备,使攻击者在不知道密钥的情况下,没有办法从算法找到突破口。
RSA算法的密钥生成过程中涉及到p,q,n, φ(n),e,d几个数字,其中p和q在最后被销毁,还剩下四个:n, φ(n),e,d,在这四个数中,n和e用于私钥,对外公开,d用于私钥要严格保密,一旦d泄露了,就等于加密系统被破解了。现在的问题是,能否通过公钥n和e推算出d?
回顾RSA密钥生成的过程,d是由ed≡1 (mod φ(n))计算得出的,只有知道e和φ(n)才能计算出d;φ(n)=(p-1)(q-1),只有知道p和q才能计算出φ(n);n=pq,GCD(p,q)=1,只有将n进行素因子分解才能计算出p和q,这就回到了RSA的原理——将两个大素数相乘很容易,但是想要对它们的乘积进行素因子分解却及其困难。反过来,如果n可以被素因子分解,就可以复原已经被销毁的的p和q,进而计算出d,获得私钥。
所谓将大整数进行素因子分解很困难,是指计算上的困难,对一极大整数做素因子分解越困难,RSA算法越可靠。假如有人找到一种快速的素因子分解算法,那么用RSA加密的可靠性就将会极度下降。到目前为止,只有短的RSA密钥才可能被解破,至今为止,人们还没有发现一个有效的方法快速分解大整数。为了确保RSA加密系统的安全性,应该随机选择两很大的素数进行操作,以确保n的二进制达到上千位,以防御未来可能出现的素因子分解技术的近进步。目前能预测2030年之前足够安全的RSA密钥长度是2048位。
攻破心的壁垒
坚固的城堡往往是从内部被攻克的,再高明的加密体制也抵挡不住私钥泄露的危险。
周武王在对主将颁布“阴符”时曾明确告知,谁要是敢泄露“阴符”的暗语就剁了谁:“诸奉使行符,稽留者,若符事泄,闻者告者,皆诛之。八符者,主将秘闻,所以阴通言语不泄,中外相知之术。”然而一旦被俘,又有几个人能够做到不泄密?因此谍战片中很少有高端的密码破解技术,更多是严刑拷打,这比破译密码有效多了。现代特种部队的“抗审”训练也并非是提高硬扛的能力,而是尽最大可能拖延泄密的时间,像挤牙膏一样把信息一点一点透露出去,因为随着时间的流逝,机密的等级也将变得越来越低。
窃取和平年代的商用密码自然不能靠严刑拷打了,我们平时接触的密码很多,比如最典型的公司门禁密码和业务系统密码。然而遗憾的是,绝大多数公司都过于注重技术上的安全性,轻视了脆弱的人心。
“银河集团”最近上线了用于管理公司业务和客户信息的“芒砀山系统”,这是由一个著名的软件公司开发的,号称能够安全运行100年。“芒砀山系统”在外网上公开了注册客户能够使用的一些功能。“银河集团”特别注重系统的安全性,要求所有有权限登录管理端的员工必须使用16位以上的密码并定期更换。现在Mallory来了,他想要到系统中游荡一番,顺便篡改一下数据,他会怎么做呢?
以下是Mallory的自述:
我一定要黑进“芒砀山系统”,为此我做了大量的信息侦查,收集到了“银河集团”一些人员的姓名和座机电话。
我不知道这个系统还有没有其它名字,所以我一开始拨打了一个客服电话,说自己的公司也在使用一个类似的系统,我说:“我们的系统在公司内部叫芒砀山,你们也叫这个名字吗?”
“我们叫芒砀山号。”客服小姐说。
这是个有用的信息,能够增加我的信誉度。然后,我给行政部门的打了一个电话,给了他们在信息侦查时找到的客服部经理的名字,说自己是一位刚刚入职的员工,需要分配一个邮箱。接电话的哥们立马给我开通了邮箱,并告诉了我邮箱地址和初始密码。
一小时后,我又拨打了行政部门的电话,接电话的还是刚才的人,我挂掉了电话。
又过了一会,我再次拨打行政部的电话,这次是一个叫赵信的人接听的。“Hi,我是客务部新入职的员工,我需要登录芒砀山号的客户管理界面,能不能为我开通一下账号?”“好的,你的邮箱是什么?”我给了他刚刚激活的邮箱。“好的,没问题。你的帐号就是你的邮箱号,初始密码需要你到我这里领取。”
我试着问:“可以把密码发到我邮箱里吗?”
他回答说:“我们不允许在电话和邮件中给你密码,你的办公室在哪里?”
我说:“我马上要去赶飞机。你可以把密码密封在一个信封里,待会交给琪琳吗?” 琪琳是我从信息侦查环节中发现的客服部秘书的名字。
他说“好的,祝你工作顺利。”
过了一会,我打电话给琪琳,取回赵信留给我的信封,并读取其中的信息给我,她照办了。我告诉她把字条扔到垃圾桶里,因为我不再需要它了。
“芒砀山系统”就这样对我敞开了大门。
Mallory使用了一种被称为“社会工程学”的知识取得了密码,从而“光明正大”地走进了系统,并不是Mallory的技术高深莫测,而是Mallory更懂人心。
注:Mallory的故事改编自世界顶级黑客凯文·米特尼克的《线上幽灵》。
来自量子计算的挑战
RSA加密系统能够确保安全的前提是,没有一个计算机能够在可接受的时间内分解一个极大整数,即使是超级计算机也要花费数年的时间。然而,随着量子计算机体系结构的发展,过去的超强算力似乎也并非不可触及。
二十世纪后期,美国学者提出了基于量子计算机的质因数分解算法——Shor算法,从理论上证明,在当前最快的计算机上需要上万年才能完成的计算任务,量子计算机瞬间即能完成,严重地威胁到了基于这类数学难题的公钥密码系统的安全性。紧随其后的Grover量子搜索算法,对于密码破译来说,相当于把密钥的长度减少一半,种种迹象表明,通用量子计算机一旦实现,对目前广泛使用的RSA、EIGamal、ECC公钥密码和DH密钥协商协议都构成了严重的威胁。
2016年,美国国家安全局建议所有美国政府机构放弃RSA加密算法,而改用其它技术。随着量子技术的不断成熟,实用量子计算机总会有到来的一天,到了那一天,密码学,特别是基于NP困难问题的公钥密码系统会何去何从呢?
作者:我是8位的