吴恩达机器学习系列理论加实践(七、正则化及matlab实践)

七、正则化

7.1过拟合问题

什么是过拟合问题，之前我们学习了线性回归、逻辑回归，他门都能够有效的解决许多问题，但是有些时候可能会遇到过拟合问题导致效果很差。
在这里将会讨论过拟合问题，他是怎么引起来的，以及通过学习一种正则化技术来改善或者减少过拟合问题。
如果我们有非常多的特征，我们通过学习得到的假设可能能够非常好地适应训练集（代价函数可能几乎为 0），但是可能会不能推广到新的数据，比如在测试集当中效果却很差。
下面看几个例子，来直观的认识一下什么是欠/过拟合：

如第一个图所示，我们拟合出一条直线，我们可以直观地看到其代价误差是比较大的，因为直线上的点与样本点之间的距离还是比较大的，而这就叫做欠拟合：也就是训练出的模型并不能很好的拟合训练数据；
第二个模型二次方曲线图相对于第一个可以看出来，其拟合的效果好很多即损失的代价很低；
而对于第三个模型四次方曲线，其接近完完全全拟合了所有的训练数据，代价误差接近于0，但是她一定就是最好的吗，试想一下当我们把这个模型用于测试数据预测时，其效果可能会非常的差。也就是说这个模型只是完美的拟合了训练数据，而当把他用于新的数据预测时，其损失代价可能会非常高，这就是所谓的过拟合。
同样对于分类模型也是如此：

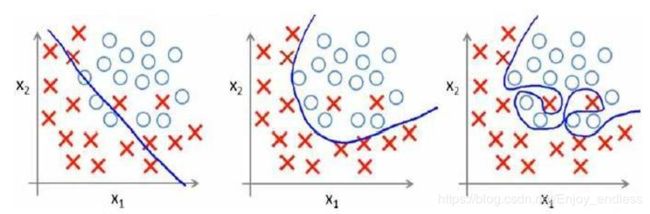
以多项式理解，x 的次数越高，拟合的越好，但相应的预测的能力就可能变差。
如果在真实场景中我们出现了如上过拟合问题，我们应该如何处理呢：

1. 丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征，或者使用一些模型选择的算法来帮忙（例如 PCA）；也就是说去掉那些过于细节、无关紧要的特征；
2. 正则化。 保留所有的特征，但是减少参数的大小。 (具体见下)

7.2代价函数

在上面图例当中我们看到了，随着高次幂的添加模型逐步走向过拟合，所以我们很直观地可以想到的就是对于那些高次幂的参数theta进行惩罚，比如修改之后的代价函数为：


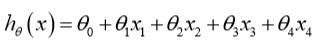
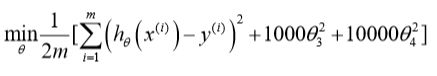
当我们最小化代价函数求得theta时，可以看出其中高次幂的theta3、theta4的值将是非常小的，从而决定了最终高次幂的值对于整体模型的影响将是很小的，也就相当于减少了过拟合的程度；
于是我们统一代价函数为：

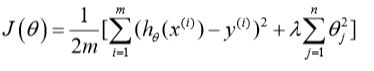
让代价函数最优化的软件来自动选择对于所有参数的不同惩罚程度(注意theta0相当于偏置不需要惩罚)。
其中lambda称为正则化参数，经过正则化处理的模型与原模型的可能对比情况如下：

在这里lambda的取值是比较关键的，因为若lambda很小的话相当于没有这个惩罚项，太大的话造成所有的参数theta都接近于0从而出现上图红色线所示情况h=theta0；

7.3正则化线性回归

在前面的学习当中，对于线性回归参数的求法我们接触了两种：1梯度下降，2正规方程；
正则化线性方程的代价函数：

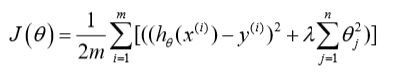
若利用梯度下降法，则我们的计算过程如下：求导然后迭代更新，注意这里的theta0需要单独处理(因为他没有惩罚，导数形式不一样)：

根据上面的更新规则我们可以发现，其实对于每次theta的更新相比较之前无正则化的更新，只是多减了一部分。惩罚参数越大减得越多。
同样我们也可以通过正规方程来求解正则化之后的线性回归模型：

7.4正则化的逻辑回归模型

逻辑回归，关于其优化算法除了梯度下降算法之外，我们还接触了其他更高级的优化算法（同样需要自己设计代价函数），根据如上原理结合逻辑回归代价函数我们可以得到正则化的逻辑回归代价函数：

利用梯度下降法：求导、迭代，我们可以发现其同线性回归的形式是一样的：

形式一样，但是注意模型h()的求法是不一样的。

%matlab代码实践

%加载数据
data=load('ex2data2.txt')
X=data(:,1:2);y=(:,3); %一二列作为X，第三列为标签y
%绘画显示
pos=find(y==1);neg=find(y==0);   %正负例坐标
plot(X(pos,1),X(pos,2),'r+','LineWidth',2,'MakerSize',4);
plot(X(neg, 1), X(neg, 2), 'ko', 'MarkerFaceColor', 'm', 'MarkerSize', 4);

%在这里我们需要注意一点，因为数据X中只给了两个特征，如果想利用
%多项式回归的话肯定是不够，所有我们可以借助多项式特征来处理，
%即将二维特征映射到多项式特征，新生成的这些变量即原有变量的有机组合，
%换句话说，当两个变量各自与y的关系并不强时候，把它们结合成为
%一个新的变量可能更会容易体现出它们与y的关系.方法如下：
function out=mapFeature(X1,X2)
degree=6  %最高次幂
out=ones(size(X1(:,1)));
for i=1:degree
	for j=0:i
		out(:,end+1)=(X1.^(i-j)).*(X2.^j);
	end
end

%规则化损失函数
function [J,grad]=costFunctionReg(theta,X,y,lambda)
m=length(y);
J=0;
grad=zeros(size(theta));
h=sigmiod(X*theta);
J=(-y*log(h)-(1-y)*log(1-h))/m+lambda*sum(power(theta(2:length(theta),:),2))/(2*m);
grad=X'*(h-y)/m;
grad=[grad(1,1);grad(2:length(theta),:)+lambda*theta(2:length(theta),:)/m]

%利用自定义损失函数及内置函数求最优参数
options=optimset('GradObj','on','MaxIter',400);
[theta,J]=fminunc(@(t)(costFunctionReg(t,X,y,lambda)),initial_theta,options);

%预测
p=predict(theta,X);
fprintf('%f\n',mean(double(p==y))*100);

这一讲主要介绍了什么是欠/过拟合、以及如何处理过拟合问题，并应用于线性、逻辑回归的训练当中，得到最终有效的结果。

下一讲：八、神经网络