深度学习入门笔记 Day8/15 误差反向传播法（二）
一、如何实现加法层和乘法层
用代码实现昨天的苹果、橘子问题。
这里的layer应该理解为节点，MulLayer是乘法节点的实现，AddLayer是加法节点的实现。
对于每个节点声明一个类变量
mul_apple_layer = MulLayer() #节点1，乘法节点，苹果单价*苹果个数
mul_orange_layer = MulLayer() #节点2，乘法节点，橘子单价*橘子个数
add_apple_orange_layer = AddLayer() #节点3，加法节点，苹果总价+橘子总价
mul_tax_layer = MulLayer() #节点4，乘法节点，总价*税率正向求得税后总价，反向求得各输入的偏导。
class MulLayer:
def __init__(self):
self.x = None
self.y = None
def forward(self, x, y): #前向，存储输入变量x，y，便于反向求偏导时使用
self.x = x
self.y = y
out = x * y
return out
def backward(self, dout):
dx = dout*self.y
dy = dout*self.x
return dx, dy
class AddLayer:
def __init__(self):
pass
def forward(self, x, y):
out = x+ y
return out
def backward(self, dout):
dx = dout*1
dy = dout*1
return dx, dy
if __name__ == '__main__':
apple = 100
apple_num = 2
orange = 150
orange_num = 3
tax = 1.1
# layer 理解成节点，图上有四个节点，声明四个class
mul_apple_layer = MulLayer()
mul_orange_layer = MulLayer()
add_apple_orange_layer = AddLayer()
mul_tax_layer = MulLayer()
# forward
apple_price = mul_apple_layer.forward(apple, apple_num)
orange_price = mul_orange_layer.forward(orange, orange_num)
all_price = add_apple_orange_layer.forward(apple_price,orange_price)
price = mul_tax_layer.forward(all_price, tax)
print(price)
# backward
dprice = 1
dall_price, dtax = mul_tax_layer.backward(dprice)
dapple_price, dorange_price = add_apple_orange_layer.backward(dall_price)
dapple, dapple_num = mul_apple_layer.backward(dapple_price)
dorange, dorange_num = mul_orange_layer.backward(dorange_price)
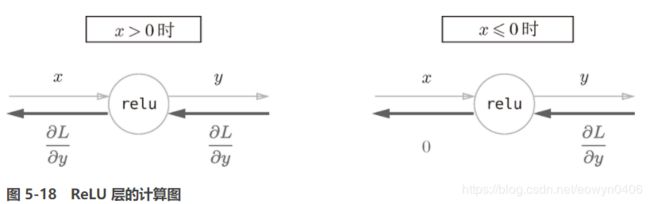
print(dapple, dapple_num, dorange, dorange_num, dtax)二、如何实现ReLU层和Sigmoid层
回顾一下ReLU函数：
他的导数：
class Relu:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0) # 判断输入中哪些元素小于等于0，mask中对应的位为True
out = x.copy() # 把输入直接拷贝给输出
out[self.mask] = 0 # 把输入中小于等于0的元素都置零
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
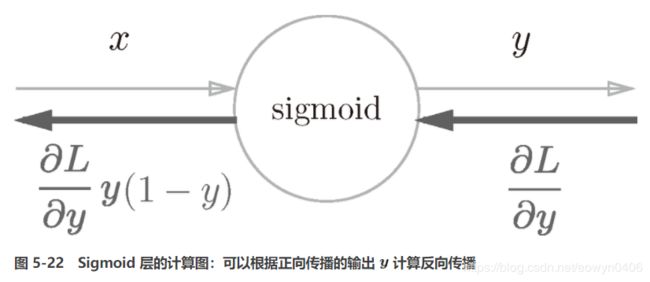
return dx同理Sigmoid函数： 
，导数：
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
out = 1 / (1 + np.exp(-x))
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dx
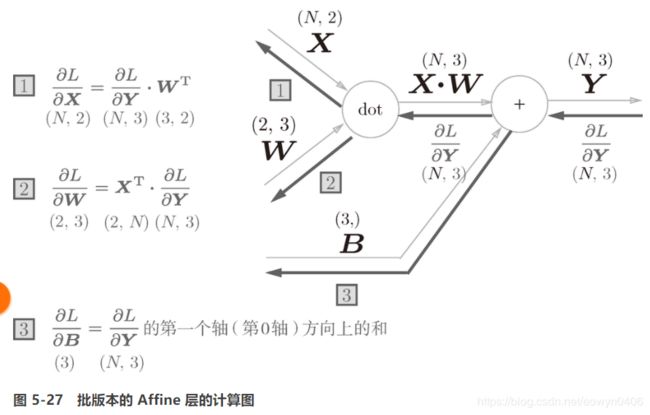
三、如何实现全连接层和Softmax层
相邻层的所有神经元之间都有连接，这称为全连接（fully-connected）。
所以书里这章的全连接指的是Affine（仿射变换：1个线性变换【加权】+1个平移【偏移】）
这里涉及到矩阵求导，不详细写了。
关于偏移，因为在一次前向计算过程中，对于每一个输入向量![X_i, i\in [1,N]](http://img.e-com-net.com/image/info8/84f76af84baa41e58a8730b4221943b1.gif){kind=small}
，他的第 
个输入 
对应的偏移量 
都是一样的，所以反向求导的时候，对于 的求导要把从1到N的导数加起来。
关于softmax的实现，需要注意的是反向传播的时候如果一个节点有多个输入，要把他们加起来。
比如除法节点 / 处反向时：
，因为 t 是one hot表示，某个输入对应的 t 有且仅有一个元素为 1，其余值均为0.
如果不用计算图的方法，用直接求导也可以推出相同的结论。
四、如何将这些层组装成一个二层神经网络
仿射层+ReLU层是神经网络的一层。因为仿射层是将输入加权、偏置，ReLU是激活函数。
而输出层是由一个Affine层+Softmax层构成。Softmax是一个分类器。
所以二层神经网络只需要Affine1+ReLU+Affine2+Softmax即可。
五、如何使用SGD更新这个网络的参数
因为每一个层都有forward和backward，因此，SGD中的predict可以由forward完成，而求gradient的时候可以由backward完成。
只需要把前面代码中的predict和gradient修改为各层的forward和backward即可。
六、三层神经网络的Python实现
下面是作者搭建的一个三层神经网络的代码（结构：Affine1+ReLU+Affine2+ReLU+Affine3+Softmax），在书中二层神经网络代码的基础上进行了一些修改（输入60000*784，W1:784*100, W2:100*50, W3: 50*10）：
import numpy as np
import matplotlib.pyplot as plt
import sys, os
sys.path.append(os.pardir)
from dataset.mnist import load_mnist
from three_layer_net import *
import datetime
starttime = datetime.datetime.now()
# x_train.shape = (60000, 784)
# t_train.shape = (60000, 10)
# x_test.shape = (10000, 784)
# t_test.shape = (10000, 10)
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label = True)
train_loss_list = []
# 超参数
iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
iter_per_epoch = 100 # max(iters_num/batch_size,1)
# initialize the net
threeLayerNet = ThreeLayerNet(x_train.shape[1],100,50,10)
trainLoss = np.zeros(iters_num)
trainAccuracy = np.zeros(iter_per_epoch)
testAccuracy = np.zeros(iter_per_epoch)
# start training
k = 0
for i in range(0,iters_num,1):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
grads = threeLayerNet.gradient(x_batch, t_batch) # backward grads
for key in ('W1', 'b1', 'W2', 'b2', 'W3', 'b3'):
threeLayerNet.params[key] -= learning_rate * grads[key]
# trainLoss[i] = threeLayerNet.loss(x_batch, t_batch)
if i%batch_size == 0:
trainAccuracy[k] = threeLayerNet.accuracy(x_train, t_train)
testAccuracy[k] = threeLayerNet.accuracy(x_test, t_test)
k += 1
endtime = datetime.datetime.now()
print("runtime = ",(endtime - starttime))
trainStep = range(0,iter_per_epoch,1)
# plt.plot(trainStep,trainLoss)
plt.plot(trainStep,trainAccuracy, 'r')
plt.plot(trainStep,testAccuracy, 'b')
plt.show()
three_layer_net.py
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
from common.layers import *
from common.gradient import numerical_gradient
from collections import OrderedDict
class ThreeLayerNet:
def __init__(self, input_size, hidden_size1,hidden_size2, output_size, weight_init_std=0.01):
# 初始化权重
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size1)
self.params['b1'] = np.zeros(hidden_size1)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size1, hidden_size2)
self.params['b2'] = np.zeros(hidden_size2)
self.params['W3'] = weight_init_std * np.random.randn(hidden_size2, output_size)
self.params['b3'] = np.zeros(output_size)
# 生成层
self.layers = OrderedDict() # 使字典按先后输入顺序有序排列
self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
self.layers['Relu1'] = Relu()
self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = Relu()
self.layers['Affine3'] = Affine(self.params['W3'], self.params['b3'])
self.lastLayer = SoftmaxWithLoss()
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
# x:输入数据, t:监督数据
def loss(self, x, t):
y = self.predict(x)
return self.lastLayer.forward(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
if t.ndim != 1: t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# x:输入数据, t:监督数据
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.lastLayer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 设定
grads = {}
grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
grads['W3'], grads['b3'] = self.layers['Affine3'].dW, self.layers['Affine3'].db
return grads
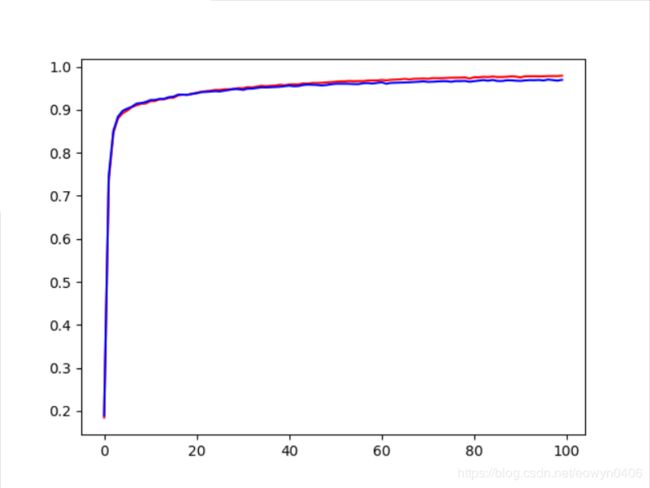
运行结果，显示训练完的网络准确度接近1，但是跟两层网络比相差不大，没有显著提升性能。
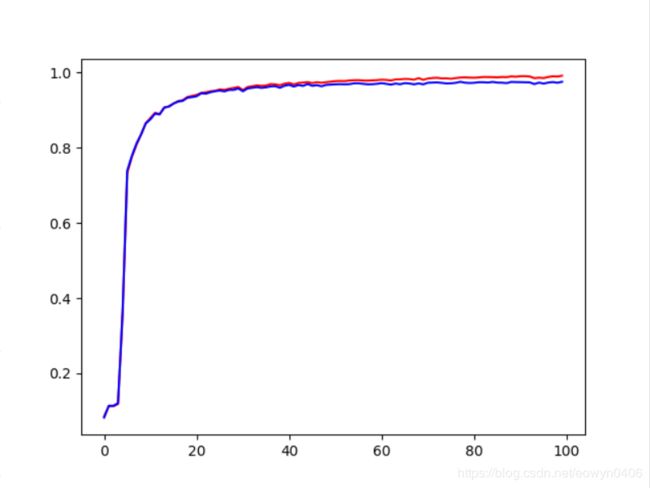 三层网络准确率 |
 两层网络准确率
|
三层网络训练时长：1分25秒；二层网络训练时长：57秒