Learning with noisy labels总结
Learning with noisy labels总结
- Deep Label Distribution Learning With Label Ambiguity
- Joint Optimization Framework for Learning with Noisy Labels
- Probabilistic End-to-end Noise Correction for Learning with Noisy Labels
- PENCIL框架
- 训练过程
- 实验结果
- cifar100
- cifar10
- CUB-200
- Clothing1M
- 总结
工作中发现大部分的时间都是在处理脏数据,而偶然中看到CVPR2019中的论文Probabilistic End-to-end Noise Correction for Learning with Noisy Labels(简称PENCIL),打算按照自己的理解总结一下这个研究方向的重要论文。
Deep Label Distribution Learning With Label Ambiguity
论文链接:https://arxiv.org/abs/1611.01731
在这篇论文里首先提出了用label distribution代替原始的noisy label用于模型训练。soft label和hard label的概念如果要追溯可以追溯到更早,比如Hinton在15年提出的蒸馏,文中就使用了从教师模型得到的输出经过平滑得到的soft label去指导学生模型训练。Deep Label Distribution Learning(简称DLDL)这篇文章则主要针对于部分应用场景中的标签模糊情况,文中举了4个例子:年龄预测、头部姿态预测、多标签分类、语义分割。

在以上提到场景中,由于标签模糊引入的脏数据几乎无可避免,如年龄预测中,25岁的人脸与24/26岁几乎不存在差异,使用原始的one-hot标签则无法表示这些边界模糊的标签之间的联系。我们希望类别相关性强弱能够从label本身体现出来,因此文中提出了使用label distribution代替one-hot label的做法及其相应的训练方法。
label distribution即把标签看成是在不同类别间的离散分布,有点类似于CNN的最终输出向量(经过了softmax),在不同类别间有一个置信度。假设网络的输出向量为 y ^ \pmb{\hat{y}} y^y^y^, y ^ \pmb{\hat{y}} y^y^y^的第 k k k个元素为 y ^ k \hat{y}_k y^k,标签分布向量为 y \pmb{y} yyy, y \pmb{y} yyy的第 k k k个元素为 y k y_k yk,论文中以Kullback-Leibler (KL) divergence来表示两个向量之间的相似程度,以 θ ∗ \pmb{\theta^*} θ∗θ∗θ∗表示最佳模型参数,则有:
(1) θ ∗ = arg min θ ∑ k y k ln y k y ^ k \pmb{\theta^*}=\arg\min_{\theta} \sum_k{y_k}\ln \frac{y_k}{\hat{y}_k} \tag 1 θ∗θ∗θ∗=argθmink∑yklny^kyk(1)
变形一下得
(2) θ ∗ = arg min θ − ∑ k y k ln y ^ k \pmb{\theta^*}=\arg\min_{\theta} -\sum_k{y_k}\ln {\hat{y}_k} \tag 2 θ∗θ∗θ∗=argθmin−k∑yklny^k(2)
所以KL loss为:
(3) T = − ∑ k y k ln y ^ k T= -\sum_k{y_k}\ln {\hat{y}_k} \tag 3 T=−k∑yklny^k(3)
这里就定义了用label distribution作为标签的训练方式,论文的后面还分析了对于此loss的梯度分析,这里不展开。
下一步是关于如何获得label distribution的设计。本文中,标签分布是人为根据数据集的特点进行设计定义的。比如在年龄估计中,以离散的正态分布值表示标签分布,其中均值为原标签值,方差则可在一定的范围内均稳定;在头部姿态估计中,标签分布是两个角度的联合概率分布,同样是正态分布,与年龄估计中的设定相似。由于这部分给定了强烈的先验信息,且对不同应用场景设计不同,个人觉得泛化性不强,这里也不展开。
总结之,这篇论文的价值在于提出了label distribution的想法和利用KL loss及标签分布训练的方法。
Joint Optimization Framework for Learning with Noisy Labels
论文链接:http://openaccess.thecvf.com/content_cvpr_2018/papers/Tanaka_Joint_Optimization_Framework_CVPR_2018_paper.pdf
这篇论文是CVPR2018的论文,细读发现其与后文将要提到CVPR2019的论文已经十分相像。其主要贡献点是三点:
- 提出了网络参数和标签联合优化的框架,利用网络输出结果更新标签,对网络在脏数据的训练改写了loss
- 给出了大学习率下网络不易过拟合于噪声的实验结论,此结论在实践中很有用
- 设计了在CIFAR-10上伪噪声的实验和Clothing1M上的真实噪声实验
上述的三点贡献都对后面的研究产生了影响。第3点看似并不算贡献,但后面的论文在此思路的基础上做了更全面的实验,已经cover了相当一部分的实际场景,个人觉得实验设计非常精彩。
下面概括描述一下此论文的思路。本篇论文使用了soft-label软标签这个词而没有使用label distribution标签分布,用词不同但两者本质上是一样的。
在一般的分类问题中,实质是通过输入 X X X和标签 Y Y Y来更新网络参数 θ \pmb{\theta} θθθ,从而最小化损失 L L L,数学表示为:
(4) min θ L ( θ ∣ X , Y ) \min_{\theta}L(\pmb\theta|X,Y) \tag 4 θminL(θθθ∣X,Y)(4)
现假设存在脏数据,即 Y Y Y存在噪声,直接优化(4)并不能得到在干净数据下的最优化结果,因为网络参数将过拟合于噪声。通过实验发现在大学习率下参数不容易过拟合于噪声,基于这一发现,论文希望通过大学习率的网络训练来修正标签中的噪声,数学表示为:
(5) min θ , Y L ( θ , Y ∣ X ) \min_{\theta,Y}L(\pmb\theta, Y|X) \tag 5 θ,YminL(θθθ,Y∣X)(5)
于是基于这一想法,论文提出了相应的框架和算法:


在每一个epoch迭代中,先固定标签去更新网络参数,然后固定网络参数去更新标签。
先说标签的更新,因为较为简单,在提出的算法框架中有硬标签的更新方式和软标签的更新方式。硬标签更新是根据网络预测的概率最高的类别去更新当前样本的标签,软标签更新是把当前网络的输出当成是新一轮迭代的标签。显然的是,直觉上硬标签就更加不稳定,论文中也通过实验证明了软标签的结果均优于硬标签,因而最后选择的是软标签。
而对于网络参数的更新,由于使用了软标签及标签更新,loss函数的写法与常规方法有所修改,式(5)中, L ( θ , Y ∣ X ) L(\pmb\theta,Y|X) L(θθθ,Y∣X)表示为:
(6) L ( θ , Y ∣ X ) = L c ( θ , Y ∣ X ) + α L p ( θ ∣ X ) + β L e ( θ ∣ X ) L(\pmb\theta,Y|X)=L_c(\pmb\theta,Y|X)+\alpha L_p(\pmb\theta|X)+\beta L_e(\pmb\theta|X) \tag 6 L(θθθ,Y∣X)=Lc(θθθ,Y∣X)+αLp(θθθ∣X)+βLe(θθθ∣X)(6)
其中 L c L_c Lc是Kullback-Leibler (KL)-divergence,表示分类损失,是损失的主要组成,与式(1)一致:
(7) L c ( θ , Y ∣ X ) = 1 n ∑ i = 1 n ∑ j = 1 c y i j log ( y i j s j ( θ , x i ) ) L_c(\pmb\theta,Y|X)=\frac{1}{n}\sum_{i=1}^{n}\sum_{j=1}^{c}y_{ij}\log(\frac{y_{ij}}{s_j}(\pmb\theta,\pmb x_i)) \tag 7 Lc(θθθ,Y∣X)=n1i=1∑nj=1∑cyijlog(sjyij(θθθ,xxxi))(7)
s j ( θ , x i ) s_j(\pmb\theta,\pmb x_i) sj(θθθ,xxxi)就是网络的输出。
L e L_e Le是一个正则化项。考虑只存在 L c L_c Lc时,每次更新 Y Y Y后,输出和标签相等, L c = 0 L_c=0 Lc=0,训练将卡在局部最优。因而加入 L e L_e Le:
(8) L e = − 1 n ∑ i = 1 n ∑ j = 1 c s j ( θ , x i ) log s j ( θ , x i ) L_e=-\frac{1}{n}\sum_{i=1}^{n}\sum_{j=1}^{c}s_j(\pmb\theta,\pmb x_i)\log s_j(\pmb\theta,\pmb x_i)\tag 8 Le=−n1i=1∑nj=1∑csj(θθθ,xxxi)logsj(θθθ,xxxi)(8)
式(8)是网络输出与其自身作交叉熵,其结果是使网络倾向于输出0或1,不至于陷入局部最优。
L p L_p Lp是另一个正则化项。论文中提及,只优化(7)可能会导致另一种极端结果,只输出一个类别。为了抑制这种情况,引入一个先验概率分布 p \pmb p ppp,表示类别在所有训练样本中的概率分布,然后优化使得训练得到的类别分别接近于 p \pmb p ppp,同样以KL-divergence表示:
(9) L p = ∑ j = 1 c p j log p j s ˉ j ( θ , X ) L_p=\sum_{j=1}^cp_j\log\frac{p_j}{\bar s_j(\pmb\theta,X)} \tag 9 Lp=j=1∑cpjlogsˉj(θθθ,X)pj(9)
其中 s ˉ ( θ , X ) \pmb{\bar s}(\pmb\theta, X) sˉsˉsˉ(θθθ,X)表示所有训练样本的网络输出平均概率分布:
(10) s ˉ ( θ , X ) = 1 n ∑ i = 1 n s ( θ , x i ) ≈ 1 B ∑ s ( θ , x ) \pmb{\bar s}(\pmb\theta, X)=\frac{1}{n}\sum_{i=1}^n\pmb s(\pmb\theta,\pmb x_i)\approx\frac{1}{B}\sum s(\pmb\theta,\pmb x) \tag {10} sˉsˉsˉ(θθθ,X)=n1i=1∑nsss(θθθ,xxxi)≈B1∑s(θθθ,xxx)(10)
B B B表示batch size,即实际上用一个batch size的样本计算来代替全部样本。
论文的实验设计部分与下面要说的一篇论文有重合,且后一篇论文更能说明问题,这里不展开。
Probabilistic End-to-end Noise Correction for Learning with Noisy Labels
论文链接:https://arxiv.org/abs/1903.07788
PENCIL框架
这篇其实是我看到的第一篇相关领域的论文,然后才往回搜其它的论文。当时对论文的想法感触很深,虽然往回对比发现并不是全部都是创新点。尽管如此,论文的主要创新点和实验设计还是很能说明问题。
论文改进于前面提到的第二篇,Joint Optimization Framework for Learning with Noisy Labels,类似地,提出了同时更新网络参数和数据标签的方法。一个最大的改进是,数据标签也同样由梯度下降和反向传播来更新。为了达到此目的,新定义了一个向量 y ~ \tilde{\pmb y} yyy~用于构建软标签:
(11) y d = softmax ( y ~ ) \pmb y^d=\text{softmax}(\tilde{\pmb y})\tag{11} yyyd=softmax(yyy~)(11)
y d \pmb y^d yyyd是生成的软标签,而通过式(11), y ~ \tilde{\pmb y} yyy~可以通过梯度下降和反向传播更新。其初始值由原始带噪声的标签初始化:
(12) y ~ = K y ^ \tilde{\pmb y}=K\hat{\pmb y} \tag {12} yyy~=Kyyy^(12)
y ^ \hat{\pmb y} yyy^是原始带噪声的标签, K K K是一个大常数,实验中取为10。
基于上述设定,论文提出了一个同时更新网络参数和标签的框架:
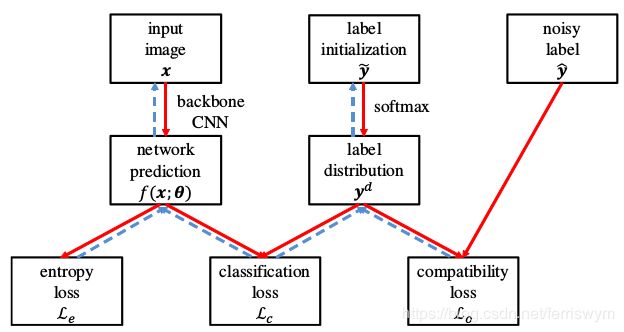
其中 f ( x ; θ ) f(\pmb x;\pmb\theta) f(xxx;θθθ)是网络经过了softmax的输出,类似于上述第二篇论文, L e L_e Le和 L o L_o Lo是惩罚项, L c L_c Lc是分类损失,为主要损失项。
(13) L c = 1 n ∑ i = 1 n ∑ j = 1 c f j ( x i ; θ ) log ( f j ( x i ; θ ) y i j d ) L_c=\frac{1}{n}\sum_{i=1}^n\sum_{j=1}^cf_j(\pmb x_i;\pmb\theta)\log (\frac{f_j(\pmb x_i;\pmb\theta)}{y^{d}_{ij}})\tag{13} Lc=n1i=1∑nj=1∑cfj(xxxi;θθθ)log(yijdfj(xxxi;θθθ))(13)
在这里 L c L_c Lc沿用了KL-divergence的形式,但是从式(13)可以看出其不符合原本KL-divergence的定义,而是写成了其对称形式,作者在文中解释这是从实验得到的结果,KL-divergence的本来形式在本框架下性能表现很差,而改用其对称形式可以得到不错的性能。此外作者从理论上分析了 L c L_c Lc的梯度:
(14) ∂ L c ∂ y i j d = − ∑ j = 1 c f j ( x i ; θ ) y i j d \frac{\partial L_c}{\partial y_{ij}^d}=-\sum_{j=1}^c\frac{f_j(\pmb x_i;\pmb\theta)}{y^{d}_{ij}}\tag{14} ∂yijd∂Lc=−j=1∑cyijdfj(xxxi;θθθ)(14)
当 f j ( x i ; θ ) ≫ y i j d f_j(\pmb x_i;\pmb\theta)\gg y^{d}_{ij} fj(xxxi;θθθ)≫yijd时,将产生一个很大的负梯度;当 f j ( x i ; θ ) ≪ y i j d f_j(\pmb x_i;\pmb\theta)\ll y^{d}_{ij} fj(xxxi;θθθ)≪yijd时,梯度接近于0。如当噪声标签为3,真实标签为7时,假设网络已经训练得到较好的特征,有 f 7 ( x i ; θ ) ≫ y i 7 d f_7(\pmb x_i;\pmb\theta)\gg y^{d}_{i7} f7(xxxi;θθθ)≫yi7d及 f 3 ( x i ; θ ) ≪ y i 3 d f_3(\pmb x_i;\pmb\theta)\ll y^{d}_{i3} f3(xxxi;θθθ)≪yi3d,根据式(14), y i 7 d y^{d}_{i7} yi7d会被增大,而 y i 3 d y^{d}_{i3} yi3d几乎保持不变,权衡了网络输出和真实标签间的差异。
L e L_e Le同式(8),为了使网络训练不至于陷入局部最优。
(15) L e = − 1 n ∑ i = 1 n ∑ j = 1 c f j ( x i ; θ ) log f j ( x i ; θ ) L_e=-\frac{1}{n}\sum_{i=1}^{n}\sum_{j=1}^{c}f_j(\pmb x_i;\pmb\theta)\log f_j(\pmb x_i;\pmb\theta)\tag {15} Le=−n1i=1∑nj=1∑cfj(xxxi;θθθ)logfj(xxxi;θθθ)(15)
L o L_o Lo则是基于了原文的一个假设,即噪声标签中正确的标签占有80%以上。
(16) L o = − 1 n ∑ i = 1 n ∑ j = 1 c y ^ i j log y i j d L_o=-\frac{1}{n}\sum_{i=1}^{n}\sum_{j=1}^{c}\hat{y}_{ij}\log y_{ij}^d\tag {16} Lo=−n1i=1∑nj=1∑cy^ijlogyijd(16)
如果噪声含量较大,可适当减少此项的权重甚至可以去掉此项。
总的损失表示为:
(17) L = 1 c L c + α L o + β c L e L=\frac{1}{c}L_c+\alpha L_o+\frac{\beta}{c}L_e\tag {17} L=c1Lc+αLo+cβLe(17)
至此,PENCIL的框架建立。
训练过程
在实际应用时,PENCIL的完整训练流程是:
- Backbone learning: 即一般深度学习的训练方式,对噪声标签应用交叉熵训练,不同的是只用大学习率训练,避免过拟合于噪声标签,得到的网络参数作为下一步训练的初始化网络参数;
- PENCIL learning: 基于式(17)用PENCIL框架进行训练,同时更新网络参数和纠正错误标签,同样只用大学习率;
- Final fine-tuning: 冻结样本的标签不再更新,把式(17)中的 α \alpha α和 β \beta β设为0,只用包含 L c L_c Lc项的loss更新网络参数,学习率衰减规则可与一般网络训练一致。
可以看到,这里只需要大学习率进行训练的过程很大程度地借鉴了第二篇论文,而实际结果也证明很有用。
实验结果
另一个大的借鉴是实验部分的设计,但在本论文中,实验更为完善也更加说明了问题。
cifar100
论文在4个数据集上做了实验。首先是cifar-100,设计了均匀噪声(Symmetric Noise)和非均匀噪声(Asymmetric Noise)两种情况。

均匀噪声是取noise rate的样本,将其标签随机打乱;非均匀噪声是取noise rate的样本,将其标签划分为下一个类别。在cifar-100这个数据集中,样本有10个大类,每个大类有10个小类,下一个类别就是其临近类别。因此这个实验设计很好地涵盖了现实数据中脏数据的两种主要来源:随机的脏数据和临近类别的脏数据。临近类别的脏数据更为普遍,就如第一篇论文所给出的场景那样。从实验结果可以看出,PENCIL可以在噪声标签下比一般方法保持更高的准确率,在临近类别的脏数据下更为明显。
因为这个实验很能说明问题,于是我自己复现了一遍,大体上按照原论文的设定,修改了三个地方:
- 原论文的Cross Entropy是没有用小学习率fine-tune的,在我的复现中按照一般学习方法进行学习率衰减;
- 原论文使用PENCIL训练网络时用的是0.35的学习率,但按照此学习率复现发现不能收敛(loss先收敛后发散,典型的学习率过大),因此我使用0.035复现,能很好收敛;
- 原论文在训练集中划分了验证集,并假设验证集也带有同样分布的噪声,但在本实验中没有使用验证集取最好结果而是直接取了最后一个epoch结果。我在复现中直接使用了全部带噪声的训练集,而以cifar-100不带噪声的测试集作为验证集,与论文一致,比较有没有验证集的差异。
复现结果如下:

从复现结果可以看到,除了在无噪声时结果稍差,在有噪声时PENCIL的优势明显,与原论文给出的结果接近。
再者,best代表训练过程中无噪声验证集最好的结果,last代表训练最后得到的结果,可以看到的是,原始的cross entropy会在训练过程过拟合于噪声,尽管loss一直在收敛,但是准确率在后面会逐渐下降,last将会比best差很多,而在实际场景下是假设验证集也有同样噪声,所以last结果更接近于实际。而PENCIL在复现过程中训练后面结果会保持平稳,实验中除了在30%asymmetric noise下准确率会下降外,其它情况last与best相差不大,因而没有在结果中给出。
cifar10
接下来再看看论文在其它数据集的情况,在cifar-10上,进行了跟第二篇论文类似的实验,也分为均匀和非均匀两种噪声:


这里的best和last指代的是带噪声的验证集的最好结果和训练到最后一个epoch的结果,由于验证集带噪声,与我自己复现的含义有所不同。这里能说明的最大问题是PENCIL不需要验证集去选取最优结果,其训练后期结果很稳定。
CUB-200
然后是在CUB-200上的测试,这个实验要说明的是在无噪声数据下算法也能保持鲁棒性。

实验给出了在不同超参下PENCIL的结果来说明其鲁棒性,能看出在合适的超参数区间下PENCIL的鲁棒性还不错。
Clothing1M
最后是在Clothing1M上的测试。原文里对这个数据集的特点描述是:1. 包含大量未知结构的噪声,估计噪声率达40%;2. 类别间严重不平衡。

论文中对这个数据集的处理是采用了伪平衡采样(pseudo-balanced sampling),因为含有噪声,所以不能保证样本的真正平衡。个人认为这里也从侧面可以看出PENCIL不能直接处理非平衡样本,显然样本的不平衡本身会严重影响网络输出的置信度,而依赖网络置信度来更新标签的方法同样也会受到很大的冲击。
总结
本文从3篇主要论文梳理了learning with noisy labels的思路发展,然后重点思考了PENCIL的框架及其在不同数据集上的结果。从第一篇论文DLDL提出标签分布(或软标签)及KL-divergence,到第二篇论文提出了同时更新网络参数和样本标签,再到PENCIL沿用梯度下降和反向传播更新标签。
在PENCIL的实验中,已经涵盖了随机出现的脏数据、临近类别的脏数据、无脏数据这三种现实数据中最常见的情况,并且显示了其鲁棒性。从其最后一个实验及其算法原理反思,目前尚未解决的是对非平衡样本的处理,而在实际情况下,即存在脏数据又存在类别不均衡的情况也十分常见。
PENCIL的框架思路实质上与实际中的“训练——清洗脏数据——再训练”的迭代过程非常相似,其想法十分自然,个人觉得其对减少数据清洗的工作量上会有很大的应用价值。