机器学习笔记(九)聚类
9.聚类
有必要回顾下前文所涉及的机器学习主流分类,有监督学习中根据预测结果离散和连续属性分为分类和回归两大类,常见的算法有:线性模型、决策树、神经网络、支持向量机、贝叶斯分类器以及集成学习。
本文开始说无监督学习(unsupervised learning),训练样本的标记信息是未知的,目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律,为进一步的数据分析提供基础。聚类(clustering)是无监督学习任务中研究最多、应用最广泛的算法。
9.1聚类任务
聚类将数据集中的样本划分为若干个通常是不相交的子集,每个子集称为一个簇(cluster),每个簇对应一个潜在概念或类别。当然这些类别在执行聚类算法之前是未知的,聚类过程是自动形成簇结构,簇所对应的概念语义由使用者命名。
形式化地说,假定样本集D={x1,x2,…,xm}包含m个无标记样本,每个样本xi={xi1; xi2;…;xin}是一个n维特征向量(属性),则聚类算法将样本集D划分为k个不相交的簇{Cl|l=1,2,…,k},其中Cl∩l≠l’Cl’=∅且D=Ul=1…kCl。相应地,用Rj∈{1,2,…,k}表示样本xj的簇标记(cluster label),即xj∈CRj。聚类的结果可用包含m个元素的簇标记向量R=(R1;R2;…;Rm)表示。
聚类既能作为一个单独过程,用于寻找数据内在的分布结构,也可作为分类等其他学习任务的前驱过程。如在一些商业应用中需对新用户的类型进行判别,但定义用户类型对商家来说可能不太容易,此时可先对用户进行聚类,根据聚类结果将每个簇定义为一个类,然后再基于这些类训练分类模型,用于判别新用户的类型。
基于不同的学习策略,可设计出多种类型的聚类算法。众多算法的评估,就先要谈两个基本问题,性能度量和距离计算。
9.2性能度量
聚类性能度量也称聚类有效性指标(validity index)。与监督学习中的性能度量作用相似。对聚类结果,要通过某种性能度量来评估其好坏。如明确最终要使用的性能度量,可直接将其作为聚类过程的优化目标,从而更好地得到符合要求的聚类结果,即事后度量也可作为事中追求的目标。
聚类将样本集D划分为若干互不相交的子集,即样本簇。怎么样的聚类结果比较好呢?物以类聚,即同一簇的样本尽可能彼此相似,不同簇的样本尽可能不同。简单来说,就是簇内相似度(intra-cluster similarity)高且簇间相似度(inter-clustersimilarity)低。
聚类性能度量大致有两类,一类是将聚类结果与某个参考模型(reference model)进行比较,称为外部指标(externel index);另一类是直接考察聚类结果而不利用任何参考模型,称为内部指标(internal index)。
对数据集D={x1,x2,…,xm},假定通过聚类给出的簇划分C={C1,C2,…,Ck},参考模型给出的簇划分为CR={CR1,CR2,…,CRk}。相应地,令F和FR表示与C和CR对应的簇标记向量。将样本两两配对考虑,定义:
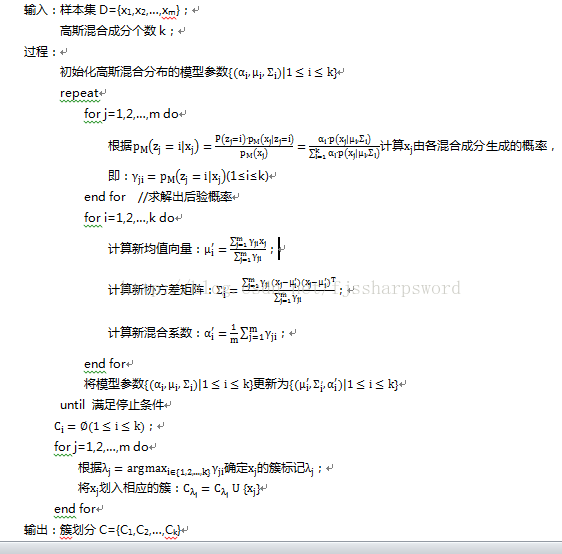
a=|SS|,SS={(xi,xj)|Fi=Fj,FRi=FRj,i b=|SD|,SD={(xi,xj)|Fi=Fj,FRi≠FRj,i c=|DS|,SD={(xi,xj)|Fi≠Fj,FRi=FRj,i d=|DD|,SD={(xi,xj)|Fi≠Fj,FRi≠FRj,i 其中集合SS包含了在C中隶属于相同簇且在CR中也隶属于相同簇的样本对,集合SD 包含了在C隶属于相同簇但在CR中隶属于不同簇的样本对,……由于每个样本对( xi,xj)(i 上文定义的性能度量指标,有non 个很重要的数学关系,就是样本间的距离dist,实际上抽象出来,任何物体的相似度都是通过距离来判断,至于怎么定义距离就不同而论。函数dist()是一个距离度量(distance measure),满足如下基本性质: 1)非负性:dist(xi,xj)≥0; 2)同一性:dist(xi,xj)=0当且仅当xi=xj; 3)对称性:dist(xi,xj)=dist(xj,xi); 4)直递性:dist(xi,xj)≤dist(xi,xk)+ dist(xk,xj); 属性通常划分为连续属性(continuous attribute)和离散属性(categoricalattribute),连续属性在定义域上有无穷多个可能的取值;后者在定义域上是有限个取值。连续属性亦称数值属性(numerical attribute);离散属性也称为列名属性(nominalattribute)。在讨论距离计算时,属性上是否定义了序的关系很重要。如定义域为{1,2,3}的离散属性与连续属性的性质更接近,能直接在属性值上计算距离,这样的属性称为有序属性(ordinal attribute);而定义域为{飞机,火车,轮船}这样的离散属性则不能直接在属性上计算距离,称为无序属性(non-ordinalattribute)。显然闵可夫斯基距离用于有序属性,那么无序属性怎么计算距离呢?实际上,有序属性和无序属性在数据挖掘上更多属性。离散属性的有序化很重要,对于机器学习来说,刻画和训练都基于向量,无序无数自然不行。 通常基于有种形式的距离定义相似度度量(similarity measure),距离越大,相似度越小。然而,用于相似度度量的距离未必一定要满足距离度量的所有基本性质,尤其是直递性。不满足直递性的距离称为非度量距离(non-metric distance),文中以人马为例来说明。本文所说的距离公式都是事先定义好的,在现实任务中,应该结合数据样本和聚类潜在结果来确定合适的距离计算公式,可通过距离度量学习(distance metric learning)来实现。 有了性能度量和距离计算,下文来说明典型的聚类算法。 文中的西瓜集例子配合起来可以更好理解算法过程。算法核心是对当前簇划分及均值向量迭代更新。 2)学习向量量化 与k均值算法类似,学习向量量化(learning vector quantization,简称LVQ)也是试图找到一组原型向量来刻画聚类结构,但与一般聚类算法不同的是,LVG假设数据样本带有类别标记,学习过程利用样本的这些监督信息来辅助聚类。 算法在对原型向量进行迭代优化,每一轮迭代中,算法随机选取一个有标记训练样本,找出与其距离最近的原型向量,并根据两者的判别标记是否一致来对原型向量进行相应的更新。若算法的停止条件已满足(如已达到最大迭代轮数,或原型向量更新很小甚至不再更新),则将当前原型向量作为最终结果返回。 上面这两个类似的算法,Kmean和LVG主要还是看样本,如果带有标记,LVG是可以采用的。文中的例子可以配合理解。 3)高斯混合聚类 与K均值、LVQ用原型向量来刻画聚类结构不同,高斯混合(Mixture-of-Gaussian)聚类采用概率模型来表达聚类原型。 对于高斯混合聚类,要理解概率密度和高斯分布才能更好理解基于概率模型的原型聚类。 算法先给给定的领域参数( )找出所有核心对象,接着以任一核心对象为出发点,找出由其密度可达的样本生成聚类簇,直到所有核心对象均被访问过为止。文中西瓜集例子可以辅助理解,最好是能就文中的西瓜集例子子集编程实现,实在时间有限,这些算法只能留待实际使用中再代码实现。 层次聚类(hierarchicalclustering)试图在不同层次对数据集进行划分,从而形成树形的聚类结构。数据的划分可采用自底向上的聚合策略,也可采用自顶向下的分拆策略。 AGNES(AGglomera-tiveNEString)是一种采用自底向上聚类策略的层次聚类算法。它先将数据集中的每个样本看做一个初始聚类簇,然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并,该过程不断重复,直至达到预设的聚类簇个数。这里的关键是如何计算聚类簇之间的距离。每个簇是一个样本集合,因此采用关于集合的某种距离即可。给定聚类簇Ci和Cj,可通过下面的公式来计算距离: 算法先对仅含一个样本的初始聚类簇和相应的距离矩阵进行初始化,接着不断合并距离最近的聚类簇,并对合并得到的聚类簇的距离矩阵进行更新,不断重复,直到达到预设的聚类簇数。9.3距离计算
9.4原型聚类
原型聚类,也称基于原型的聚类(prototype-based clustering),该类算法假设聚类结构能够通过一组原型刻画,在现实聚类任务中较为常用。一般情形下,算法先对原型进行初始化,然后对原型进行迭代更新求解。采用不同的原型表示、不同的求解方式,将产生不同的算法。

9.5密度聚类
密度聚类,也称为基于密度的聚类(density-based clustering),该类算法假设聚类结构能通过样本分布的紧密程度确定。一般情形下,密度聚类算法从样本密度的角度来考察样本之间的可连接性,并基于可连接样本不断扩展聚类簇以获得最终的聚类结果。
9.6层次聚类