开发杂谈：说说数据结构和算法的那点事儿

程序设计的本质是对确定问题选择一个好的数据结构，加上设计一个好的算法，程序设计 = 数据结构 + 算法

本文出自门心叼龙的博客，属于原创类容，转载请注明出处。https://menxindiaolong.blog.csdn.net/article/details/96620117

上个月我在公司面试了两个Android程序员，都是工作了四五年的程序员，面试一开始就问到了数据结构问题，常用的数据结构都有哪些？小伙子直接说数据结构在自己平时开发的时候根本就用不上。

在我们日常开发过程中，很多时候只关注界面和用户体验，对数据结构和算法这块要求并不高，很多程序员codeing能力很强，但一问到一些底层基础知识就发蒙，很多程序员抱怨面试造飞机，实际工作拧螺丝，面试问的基础知识与实际工作毫无联系，但公司的真正目的是在考察你的基本功，以此来判断你之后能否成长为他们最终需要的高级人才，数据结构与算法这是编程基础，基础不牢，地动山摇。

可能有些人会质疑：数据底层存储结构都不理解，codeing能力能很强？其实这也见怪不怪，就好比有人他的开车技术很高超，开的很溜，但是发动机的工作原理它懂吗？他不懂，但是他车开的确实很好，写程序也是一样的道理，有的程序员他就停留在用的阶段，用的很熟练，但是底层原理他不一定知道，再之干这一样非科班出身、转行做技术的程序员也不在少数，有的培训机构出来的，他们不一定都会先去专业的去学习数据结构和算法，这就会导致有些人工作好几年了，但是对数据结构这块的知识还是一知半解。

在去年的9月份，阿里巴巴搞了一个全球数学竞赛，一石激起千层浪，各路豪杰纷纷参战，移动互联网的狂潮已经结束了，下一个风口将是人工智能，搞人工智能就离不开数学算法，阿里醉翁之意不在酒，而在抢夺全球的顶尖级数学人才，可见算法的重要性。

在后移动互联网时代我的一些思考这篇文章我曾说过，初级程序员写UI，中级程序员写框架，高级程序员写算法，写程序写到最后都是在写算法，程序员最后拼的都是算法，在人类发展的历史长河中，我们的前辈给我们留下了很多很经典的算法，这都是人类智慧的结晶，有人写了一篇文章细数二十世纪最伟大的10大算法，感兴趣的可以去看一看。既然数据结构和算法这么重要，那么今天我决定写一篇关于数据结构和算法的入门文章，起到抛砖引玉的作用，希望你能够喜欢上数据结构和算法。

什么是数据

说到数据我们很容易就会想到：整型，浮点型，还包括音频，视频，图像，这都是数据，整型，浮点型可以进行数值运算，音频，视频，图像数据可以通过编码手段手段变成字符数据来处理，他们都有一个共同的特点，可以输入到计算机当中，能被计算机程序处理。

什么是数据结构

数据相互之间存在一种或多种特定关系的数据元素的集合，这是数据结构的概念，我们可以概括为四个字就是“数据集合”，他是一堆数据，而不是一个数据，另外数据和数据之间存在一定的关系，这种关系是指一对一的关系，或一对多的关系，或者多对对的关系，编写一个好的程序必须要分析待处理数据对象的特性以及各处理数据对象之间存在的关系，这也是就研究数据结构的意义所在。

数据结构的分类

数据结构分为逻辑机构和物理结构

逻辑结构：数据元素之间存在的关系

• 1.集合结构：集合结构中的元素除了属于一个集合之外，他们之间没有其他的关系，各个数据元素是平等的，他们共同的属性就是“属于同一个集合”
  
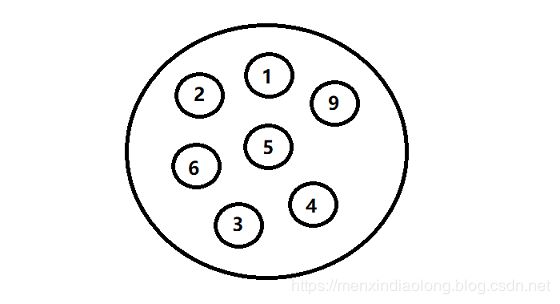
• 2.线性结构：线性结构中的数据元素之间是一对一的关系
  
• 3.树形结构：树形结构中的数据元素之间是一种一对多的层次关系
  
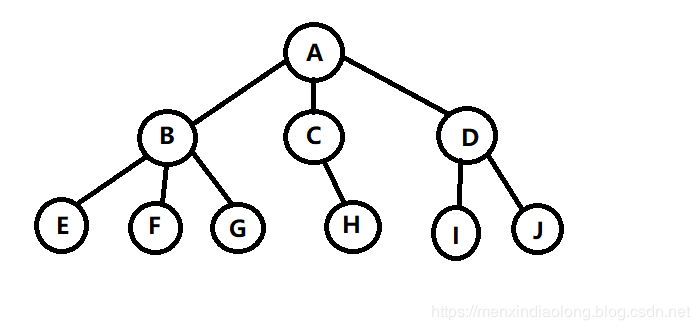
• 4.图形结构：图形结构中的数据元素之间是一种多对多的关系
  

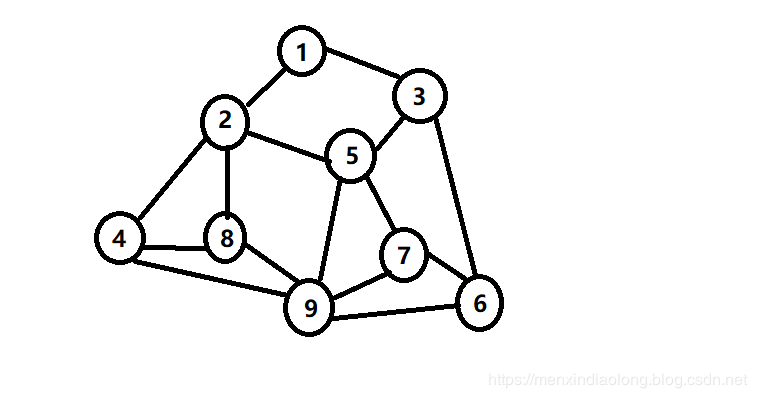
物理结构：是指数据的逻辑结构在计算机中的存储形式

• 1.顺序存储结构：是把元素存在地址连续的存储单元里，其数据间的逻辑关系和物理关系是一致的，这种数据结构很简单，就是排队站位，大家都按照顺序排好，每个人占一小段空间，大家谁也别插谁的队，数组就是这样的数据结构。当你告诉计算机，你要建立一个有9个元素的数组时，计算式就在内存中找了片空地，按照一个整形所占位置的大小乘以9，开辟一段连续的内存空间，于是第一个数组元素就放在第一个位置，第二个元素放在第二个位置，这样依次摆放。
  
• 2.链式存储结构
  在日常生活有很多这样的情况，我们去银行办理业务，或者去火车站去买票，都有这样的经历，一会儿有人插队，一会儿有人上厕所放弃排队，这样队伍当中就会添加新的成员，也有可能去掉老的元素，整个结构时刻都处于变化当中，显然，面对这样时长要变化的数据结构，顺序存储是不科学的。

于是现在的银行，医院等地方，设置了排队系统，也就是每个人去了，先领一个号，等着叫号，叫到时再去办理业务或看病。在等待的时候，你爱在哪在哪，可以坐着，可以站着，甚至可以出去转一圈，只要及时回来就可以，你关注的是前一个号有没有叫到，叫到了，下一个就轮到你了。

而链式结构和上面据的例子非常的类似，把数据元素存储在任意的存储单元里，这组存储单元可以是连续的，也可以是不连续的。数据元素的存储关系并不能反映数据元素的逻辑关系，因此需要一个指针在存储元素的地址，这样通过地址就可以找到相关联数据元素的位置。很显然，链式存储就灵活多了， 数据存在哪里并不重要，只要有一个指针存放了相应的地址就能找到它了。

逻辑结构是面向问题的，而物理结构是面向计算机的，其基本的目标就要要把数据及逻辑关系存储存储到计算机内存当中。

数据类型

上面我们谈到了数据的存储问题，在计算机当中，内存也不是无限大的，你要计算一个1+1=2这样的整形数字的加法问题，显然不需要开辟很大的内存空间，于是就需要对数据进行分类，不同的数据类型占用了不同的存储空间大小。
java中八种基本数据类型所分配的存储空间大小：

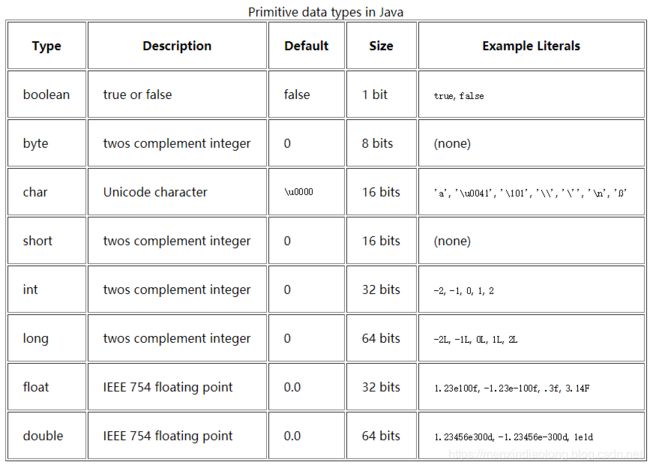
基本数据类型的取值范围：

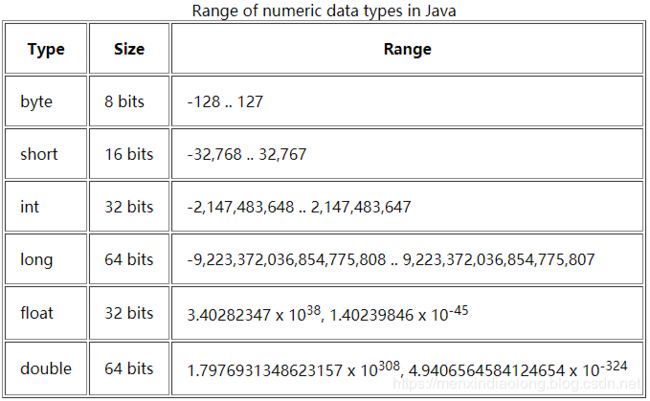
算法

讲完了数据结构的概念和分类，我们再来看看什么是算法，我们都听过高斯的故事，高斯9岁的时候，用很短的时间计算出了小学老师布置的任务：对自然数从1到100的求和。他所使用的方法是：对50对构造成和为101的数列求和（1+100，2+99，3+98……），同时得到结果：5050，高斯的求解的过程就是算法实现的过程，算法即“计算方法”，是解决特定问题所需要的步骤，在计算机中表现为指令的有限序列，每条指令表示一个或者多个操作。

int sum = 0;
    for(int i = 0; i < = 100; i++) {
	sum += i;
} 

上面这段代码就是1到100求和在计算机中的求解过程

算法特性

算法具有五个基本特性：输入、输出、有穷性、确定性和可行性，输入和出处比较容易理解的

• 输入：算法具有零个或者多个输入
• 输出：算法至少有一个或者多个输出。
• 有穷性：是指算法在执行有限的步骤之后，自动结束而不会出现无限循环，并且每一个步骤都在可以接受的时间内完成
• 确定性：算法的每一步都有确定的含义，不会产生二义性
• 可行性：算法的每一步都能通过有限的次数完成

算法的性能

衡量一个算法好坏的标准就是算法复杂度，算法复杂度分为时间复杂度和空间复杂度，时间复杂度是指执行算法所需要的时间 ；而空间复杂度是指执行这个算法所需要的内存空间。
1. 时间复杂度：

• 常数阶：

int num = 0，n  = 100;
sum = (1+n)*n/2;
System.out.println("value:"+sum);

无论n为多少，这段程序的执行次数始终是3，所以他的时间复杂度为常数阶：O(1)

• 线性阶：

for(int i = 0; i < n ; i++){
      System.out.println("value:"+i);
}

这段代码，他的循环时间复杂度为O(n),因为循环体中的代码需要执行n次

• 对数阶：

int count = 1；
    while(count < n){
    	count = count * 2;
 }

由于每次count乘以2之后，就距离n更近了一些，也就是说，有多少个2相乘以后大于n，则会退出循环，2的x次方 = n 得到 x = log2n，所以这个循环的复杂度为O(logn);

• 平方阶

 int i ,j;
 for(i = 0; i < n ; i++){
    	for(j = 0; j < n ; j++){
    		System.out.println("");
    	}
 }

外层循环的次数为n次，外层每循环一次内层循环的次数为n次，所以这段代码的时间复杂度为O(n²)

常见的时间复杂度列表

名称	运行时间
常数阶	O(1)
对数阶	O(logn)
线性阶	O(n)
nlogn阶	O(nlogn)
平方阶	O(n²)
立方阶	O(n³)
指数阶	O(2ⁿ)

常用的时间复杂度所耗费的时间由小到大依次是：
O(1)

2. 空间复杂度：
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度，记做S(n)=O(f(n))。比如直接插入排序的时间复杂度是O(n^2),空间复杂度是O(1) 。而一般的递归算法就要有O(n)的空间复杂度了，因为每次递归都要存储返回信息。一个算法的优劣主要从算法的执行时间和所需要占用的存储空间两个方面衡量。

3.时间复杂度和空间复杂度的相互关系
对于一个算法，时间复杂度和空间复杂度往往是相互影响的。当追求一个较好的时间复杂度时，可能会使空间复杂度的性能变差，即可能导致占用较多的存储空间；反之，当追求一个较好的空间复杂度时，可能会使时间复杂度的性能变差，即可能导致占用较长的运行时间。另外，算法的所有性能之间都存在着或多或少的相互影响。因此，当设计一个算法(特别是大型算法)时，要综合考虑算法的各项性能，算法的使用频率，算法处理的数据量的大小，算法描述语言的特性，算法运行的机器系统环境等各方面因素，才能够设计出比较好的算法。

数据结构和算法的关系

数据结构是算法实现的基础，算法总是要依赖于某种数据结构来实现的。往往是在发展一种算法的时候，构建了适合于这种算法的数据结构。 算法的操作对象是数据结构。算法的设计和选择要同时结合数据结构，简单地说数据结构的设计就是选择存储方式。算法设计的实质就是对实际问题要处理的数据选择一种恰当的存储结构，并在选定的存储结构上设计一个好的算法。算法设计必须考虑到数据结构，算法设计是不可能独立于数据结构的。

常见的数据结构

1.线性表

存储方式	概念	时间性能	空间性能
顺序存储	一段连续的存储单元	查找快，插入慢，删除慢 查找：常数阶O(1) 插入：线性阶O(n) 删除：线性阶O(n)	需要事先分配存储空间 分大了浪费，分小了容易溢出
链式存储	一组任意的存储单元	查找慢，插入快，删除快 查找：线性阶O(n) 插入：常数阶O(1) 删除：常数阶O(1)	有需要的时候分配存储空间 元素个数不受限制

2.栈和队列

存储方式	概念	时间性能	空间性能
栈	只能在表尾进行 添加和删除的线性数据结构	根据存储结构决定	根据存储结构决定
队列	只能在一端进行插入操作 另一端进行删除操作的线性数据结构	根据存储结构决定	根据存储结构决定

3.树
前面我们一直在讲一对一的线程数据结构，现实中还有很多一对多的情况，具有一定层次关系的数据元素的集合就是树，我觉得如果你不是做很底层的开发（比如操作系统文件管理，数据库之类的），也不是专门搞算法的，用处不会很大，事实上很多高级树结构都是为了数据库而开发的，因为数据库要很高的效率。

4.图
在线性表中，数据元素之间是被串起来的，仅有线性关系，每个元素只有一个直接前驱和直接后继。在树形结构中，数据元素之间有明显的层次关系并且每一层上的数据元素可能和下一层多个元素有关，但只能和上一层中的一个元素相关。这和一对父母可以有多个孩子，但每个孩子却只能有一对父母是一个道理。可现实中，人与人之间的关系非常复杂，比如我认识的朋友，他们之间也可能相互认知，这就不是简单的一对一，一对多的关系了，研究人际关系自然会考虑多对多的情况，这种数据结构就是图，图是一种比线性表和树更加复杂的数据结构，在图的数据结构中，节点之间的关系可以是任意的，图中的任意两个元素之间都有可能有关。

Java数据结构框架类图

1.单列表

2.双列表

我们在前面提到的集合其实是有很多用途的，散列表也算是集合的一种，为什么需要散列表呢？实际上顺序存储结构需要一个一个的按顺序访问元素，当数据总量比较大，而且这个元素比较靠后的，性能就会降低。那么散列表是一种空间换时间的存储结构，我们想一下，若在手机的通讯录中查找一个人，那我们应该不会从第一个人一直找下去，因为这样实在太慢了。我们其实是这样做的，首先看这个人的首字母是什么，比如姓张，那么我们一定会滑倒最后，因为“Z”姓的名字都在后面，还有在查字典时，要查找一个单词，肯定不会从头翻到尾，而是首先通过这个单词的首字母，找到第二个字母，第三个字母…这样可以快速的跳到那个单词所在的页。其实这就是散列表的思想，散列表，又叫哈希表，是能够通过给定的关键字的值直接访问到具体对应值得一个数据结构。也就是说，把关键字映射到一个表中的位置来直接访问记录，以加快访问的速度。

总结

我们从数据，数据结构，算法，数据结构和算法的关系，常见的数据结构，Java数据结构框架这六个方面，循序渐进把把数据结构和算法基本就讲完了，大家也有个大致的了解，其实数据结构和算法涉及到的知识点远远不止这一点，我只是挑了一些工作实战中常用的数据结构讲了一下，以后还需要大量的算法练习来提升自己的算法内功修炼，做了这么多年技术，我一直在思考，我们每天在codeing到底在做什么？其实程序设计的本质是对确定问题选择一个好的数据结构，加上设计一个好的算法，就这么简单，程序设计 = 数据结构 + 算法。