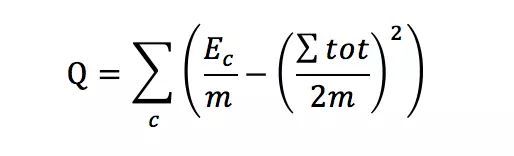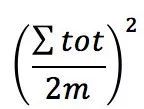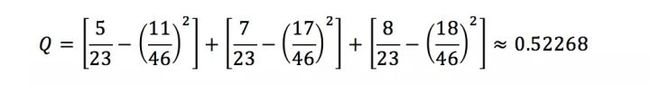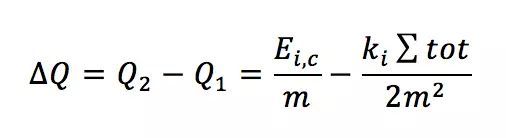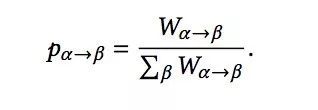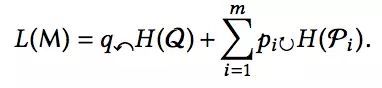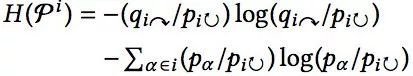社区检测与高密子图挖掘(上)
前面我们说过图的第二个优点是拉帮结派,在图里面是很容易形成团伙结构,近年来,研究这个问题的论文也是汗牛充栋。本章,我们就这一问题所衍生出来的两个方向:社区检测(Community Detection)和高密子图挖掘(Dense Subgraph Mining)作相关讲解。
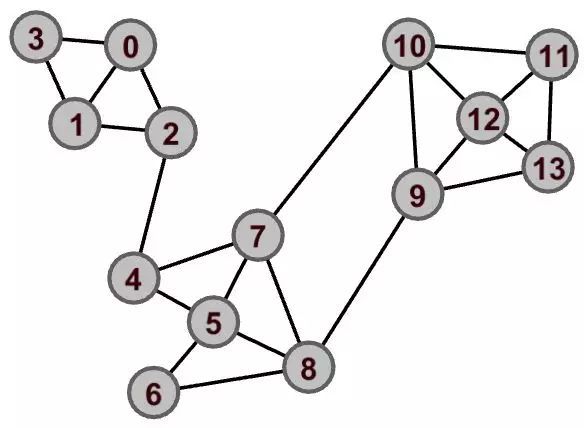
本文,我们先讲社区检测的相关算法。社区检测的任务是什么呢?举个例子,给定如下图。
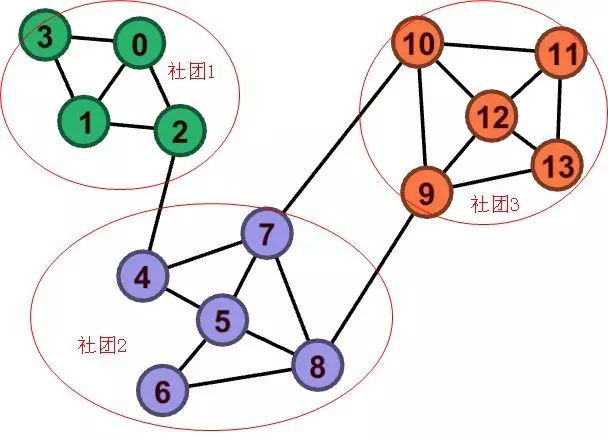
直观印象告诉我们,该图存在以下的社区结构:
像这样,从给定图中,将各节点划分到相应社团的任务称为社区检测。值得注意的一点是,一般当我们在说社区检测的时候,节点都是同态的,类型都一样。
本文会重点介绍三个最流行的社区检测算法Louvain、Lpa、Infomap,最后对社区检测作一些补充说明。
Louvain算法
Louvain算法是一种基于模块度的社区检测算法,由于其良好的效率与稳定性而广受欢迎。网上也有基于Spark GraphX 的开源实现版本。
模块度(Modularity)
同很多无监督的聚类算法一样,衡量指标是一个至关重要的因素,很多时候,我们只需要定义好这个指标,然后选择启发式的更新方法去不断优化这个值。一个算法的大概骨架也就出来了。当然一个好的社区衡量指标要符合基本逻辑:社区内联系紧密,社区间联系松散。在06年《Modularity and Community structure in networks 》一文中,作者Newman 给出了如下Modularity的定义:
m表示图中边的数量;
c表示某个社区;
Ec表示社区c内边的数量;
表示社区c节点的度之和(包含与其他社区相连边的度)
可以这样去理解上面这个公式:
表示实际情况下,c社区内产生边的概率
表示在一种理想情况下,给定任意节点i的的度ki,对节点i和节点j进行随机连边,边属于社区c的概率期望
于是上式就表示了社区内连边数与随机期望的一个差值。连边数比随机期望值越高,表明社区划分的越好。
比如上图中的:
有了上述模块度的定义作为铺垫,Louvain算法就可以启发式地去最大化Q值了。
Louvain算法步骤
- 初始化,将图中的每个节点看成一个独立的社区;
- 对每个节点,依次尝试把节点i分配到其邻居节点所在的这个社区计算分配之前与分配之后的模块度变化△Q,并记录△Q最大的社区,如果Max△Q>0,则将该节点分配到该社区;
- 重复第二步,直到所有节点的所属社区不再变化。
我们看第2步,很像决策树生长时计算信息熵取最大增益一样,假设节点i移动到社区c;
移动前模块度
移动后模块度
可以看到,△Q的计算只与节点i和社区c的连边有关,所以这个计算是非常快的,并且也比较容易并行处理。
最后,Louvain算法也可以分层进行,将每一次Louvain算法检测出来的社区进行压缩处理成一个新的节点,重新构图,继续跑Louvain算法,这样就可以得到层次化的社区标签了。
LPA-Label Propagation Algorithm
LPA算法是一个极其简单的图传播算法,其经验假设是以节点为中心,进行投票制,十分高效。
算法过程
- 初始化,将图中的每个节点看成一个独立的社区;
- While所有节点的社区标签不再变化;
- 统计每个节点邻居的社区,将出现最多次的社区赋给该节点,如果出现最多次的社区有多个,随机选择一个社区赋给该节点。
算法本身很简单,分布式实现也很容易。但是这个算法也存在很大的问题:由于存在随机选择的情况,所以算法很容易出现振荡。但这个算法的运行开销很低,拿来做baseline,作为参考也是可以的。另外,对于一个带权重的图,亦可以考虑带权重的投票机制。
Infomap算法
这个算法又称map equation,是个思路十分清奇的算法。从信息论的角度出发,假设一个random worker 在图上进行随机游走,那么怎么用最少的编码长度来表示其路径呢?也即最小平均比特(minimize bits per step)。一个基本的经验是:
◻如果节点没有社区结构,那么直接根据每个节点的到达概率,调用香农信息熵公式,就可以得到理论上的最小平均比特;
◻如果节点存在社区结构,那么社区内的节点就可以共享社区的bit位码,这相当于其本身可以用更少的位码来表示,所以相比没有社区结构的情况,可以得到更小的平均比特;
社区划分的越好,那么表示任意一条随机游走的路径所需的平均比特就越小。
OK,现在的问题就可以转化为如何在数学上量化这个平均比特,如果我们能量化这个衡量标准,那么整个算法的框架就跟前面 Louvain 算法几乎一致,不断改变节点的社区划分,启发式地去最小化平均比特。
那么首先我们来看看最简单的情况,所有节点都属一个社区的时候怎么去量化平均比特?
由于节点都在一个社区,所以随机游走每一步都只能是在节点之间行走,不存在进出其他社区的事件发生,如果我们能够计算出每个节点的到达概率,就可以依据信息熵的公式来量化平均比特了:
这里pα表示节点α的到达概率:
给定一个有向权重图,节点的到达概率怎么计算呢?
一个暴力的办法是在图上进行长时间的随机游走,最后统计每个节点的出现概率。这个方法很好理解,但是在实际应用中,如果图很大,那就很难奏效了。
其实我们在第二章讲到PageRank算法时,就已经计算出了这个值。这里我们简单回顾下,假设节点 α 指向 节点 β 的边的权重为:
![]()
那么节点 α 到 节点 β转移概率:
节点 α 的到达概率:
那么只要我们初始化了每个节点的到达概率之后,就可以依据上述两式不断交替迭代式地更新每个节点的到达概率,这个结果会很快趋于收敛。
跟PageRank 算法一样考虑到 DeadEnds和Spider traps的问题,需要一个假想的在整个图上的随机跳转概率,所以实际上节点α 达到概率的更新公式为:
τ 是一个超参数,表示发生随机跳转的概率,一般取0.15。
这样对计算完的
![]()
进行归一化处理,然后带到上面信息熵的公式,就可以计算出理论上同属一个社区时的最小平均比特了。
现在我们来看一般情况,假设图被划分成 m 个社区,那么每走一步就可能是以下三种事件中的一种情况:进入某个社区、从某个社区中出来、在社区内部节点间转移。现在我们来定义这三个事件发生的概率:
在社区内从节点α 转移到节点 β 的概率:
进入某个社区 i 的概率:
从某个社区 i 中出来的概率:
有了上面三种事件的概率定义,结合信息熵公式,我们一样可以计算出平均比特了。下面我们直接给出计算公式并给出相关参数的意义解释:
将图划分成 m 个社区,编码随机游走路径时的平均比特;
产生进入社区这种事件的总概率;
进入社区事件发生的信息熵;
![]()
random worker在社区 i 内部的概率,这里包括了在社区内跳转和离开该社区两类事件;
random worker 下一步事件发生在社区 i 内部的信息熵;
上面的这个式子就是Infomap算法的核心,亦称之为 map equation。其本质就是从信息论的角度出发,定义清楚各类事件的发生概率,依据信息熵公式,就可以得到此时编码所需的平均比特了。
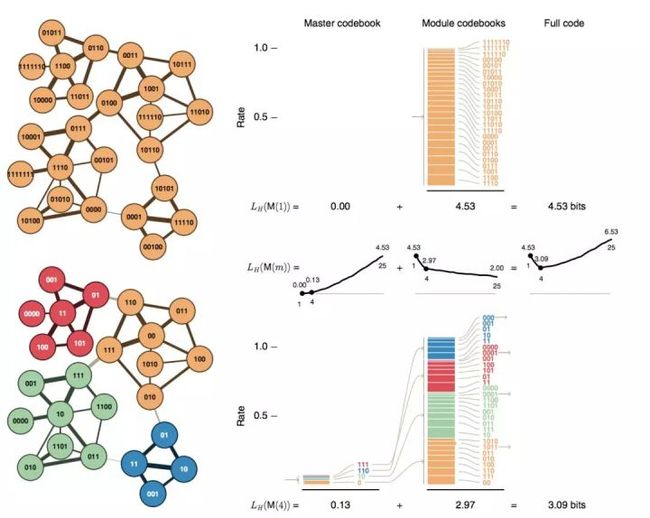
上面这个图就是在不同划分时候的平均比特的值了,可以看到,同属一个社区的时候,编码需要的平均比特为 4.53 bits, 如果按照左下图所示,将图划分成4个社区,编码所需的平均比特只需要3.09bits。值得注意的是,这里依据概率和Huffman编码算法给出了各节点具体的code,实际我们在使用Infomap的时候,并不需要显式地把每类事件都编码出来,只需要将各种概率带入公式计算出平均比特,就知道此时划分的效果好坏了。
Infomap算法的迭代过程
- 初始化,对每个节点都视作独立的社区;
- while 平均比特的值不再下降;
- 对图里的节点随机采样出一个序列,按顺序依次尝试将每个节点赋给邻居节点所在的社区,取平均比特下降最大时的社区赋给该节点,如果没有下降,该节点的社区不变。
Infomap 算法是一个十分优秀的算法,同样支持层次化的社区划分,也是三个算法里面唯一支持有向图的,论文作者也开源了C++ 版本的实现代码:
http://www.mapequation.org/code.html
另外作者也设计了一个动态展示demo:
http://www.mapequation.org/apps/MapDemo.html
demo的相关说明 :
http://www.mapequation.org/assets/publications/mapequationtutorial.pdf
总结
关于社区检测的算法,上面已经介绍了三类。其中Louvain 和Infomap 算法都是基于一个合理的全局衡量指标对社区的划分不断进行启发式的优化。如果从聚类的角度去看待社区检测,那么一个基本的范式就是首先得到每个节点的特征表达,然后基于各种聚类算法进行聚类从而得到社区的划分。这里,节点的特征表达可以从图的拉普拉斯矩阵获得,这类方法称为谱方法;也可以由 graph embedding 的方式习得每个节点的向量表达,这些相关的方法我们会在后续的相关章节进行讲解。
欢迎关注我们的微信公众号:geetest_jy 添加技术助理,一起分享交流:geetest1024