TensorFlow可视化梯度下降/公式调参
本篇博客主要介绍TensorFlow中的可视化梯度下降和参数调参。
首先是可视化梯度下降,使用的是python中Axes3d模块。
示例代码:
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
LR = 0.01
REAL_PARAMS = [1.2, 2.5]
INIT_PARAMS = [[5, 4],
[5, 1],
[2, 4.5]][2]
x = np.linspace(-1, 1, 200, dtype=np.float32)
# test 1
y_fun = lambda a, b: a * x + b
tf_y_fun = lambda a, b: a * x + b
noise = np.random.randn(200) / 10
y = y_fun(*REAL_PARAMS) + noise
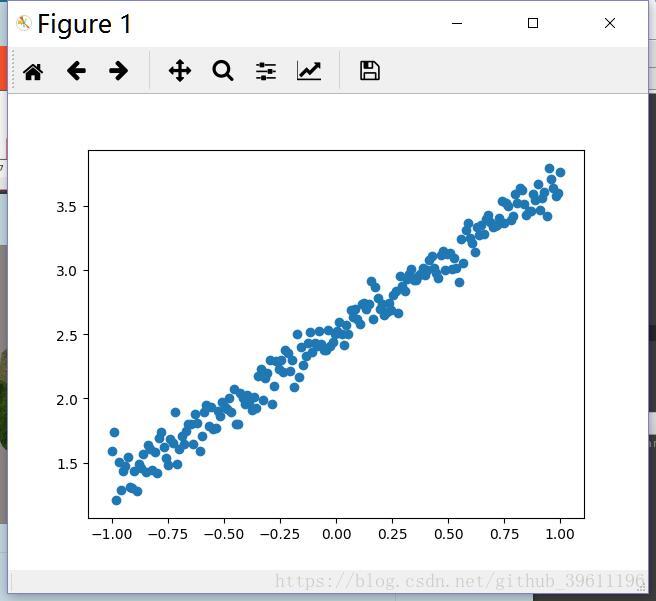
plt.scatter(x, y)
plt.show()
a, b = [tf.Variable(initial_value=p, dtype=tf.float32)
for p in INIT_PARAMS]
pred = tf_y_fun(a, b)
mse = tf.reduce_mean(tf.square(y - pred))
train_op = tf.train.GradientDescentOptimizer(LR).minimize(mse)
a_list, b_list, cost_list = [], [], []
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for t in range(400):
a_, b_, mse_ = sess.run([a, b, mse])
a_list.append(a_)
b_list.append(b_)
cost_list.append(mse_)
result, _ = sess.run([pred, train_op])
#
print('a=', a_, 'b=', b_)
plt.figure(1)
plt.scatter(x, y, c='b')
plt.plot(x, result, 'r-', lw=2)
fig = plt.figure(2)
ax = Axes3D(fig)
a3d, b3d = np.meshgrid(np.linspace(-2, 7, 30), np.linspace(-2, 7, 30))
cost3d = np.array([np.mean(np.square(y_fun(a_, b_) - y)) for a_, b_ in zip(a3d.flatten(), b3d.flatten())]).reshape(a3d.shape)
ax.plot_surface(a3d, b3d, cost3d, rstride=1, cstride=1, cmap=plt.get_cmap('rainbow'), alpha=0.5)
ax.scatter(a_list[0], b_list[0], zs=cost_list[0], s=300, c='r')
ax.set_xlabel('a')
ax.set_ylabel('b')
ax.plot(a_list, b_list, zs=cost_list, zdir='z', c='r', lw=3) # plot 3D gradient descent
plt.show()
输入数据:
拟合结果:
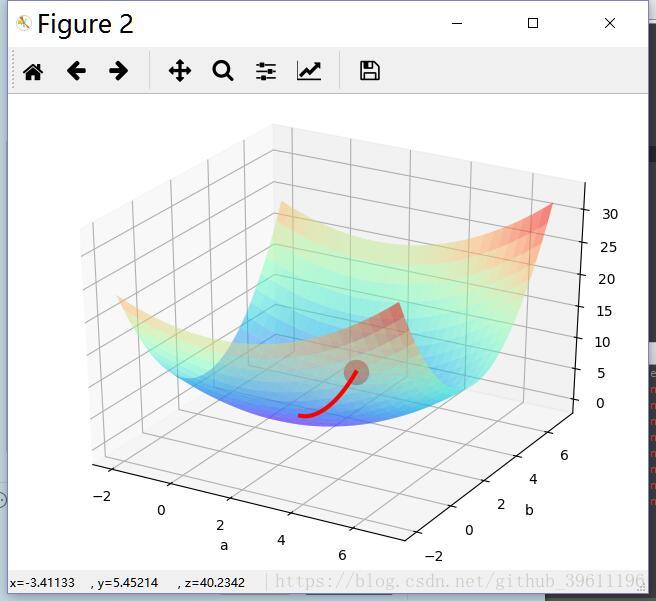
梯度下降可视化:
调参,可以根据最终显示的梯度下降图,选择合适的初始化参数,初始化参数决定了最终是收敛到局部最优解还是全局最优解:
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
LR = 0.01
REAL_PARAMS = [1.2, 2.5]
INIT_PARAMS = [[5, 4],
[5, 1],
[2, 4.5]][2]
x = np.linspace(-1, 1, 200, dtype=np.float32)
# test 1
# y_fun = lambda a, b: a * x ** 3 + b * x ** 2
# tf_y_fun = lambda a, b: a * x ** 3 + b * x ** 2
y_fun = lambda a, b: np.sin(b * np.cos(a * x))
tf_y_fun = lambda a, b: tf.sin(b * tf.cos(a * x))
noise = np.random.randn(200) / 10
y = y_fun(*REAL_PARAMS) + noise
plt.scatter(x, y)
plt.show()
a, b = [tf.Variable(initial_value=p, dtype=tf.float32)
for p in INIT_PARAMS]
pred = tf_y_fun(a, b)
mse = tf.reduce_mean(tf.square(y - pred))
train_op = tf.train.GradientDescentOptimizer(LR).minimize(mse)
a_list, b_list, cost_list = [], [], []
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for t in range(400):
a_, b_, mse_ = sess.run([a, b, mse])
a_list.append(a_)
b_list.append(b_)
cost_list.append(mse_)
result, _ = sess.run([pred, train_op])
#
print('a=', a_, 'b=', b_)
plt.figure(1)
plt.scatter(x, y, c='b')
plt.plot(x, result, 'r-', lw=2)
fig = plt.figure(2)
ax = Axes3D(fig)
a3d, b3d = np.meshgrid(np.linspace(-2, 7, 30), np.linspace(-2, 7, 30))
cost3d = np.array([np.mean(np.square(y_fun(a_, b_) - y)) for a_, b_ in zip(a3d.flatten(), b3d.flatten())]).reshape(a3d.shape)
ax.plot_surface(a3d, b3d, cost3d, rstride=1, cstride=1, cmap=plt.get_cmap('rainbow'), alpha=0.5)
ax.scatter(a_list[0], b_list[0], zs=cost_list[0], s=300, c='r')
ax.set_xlabel('a')
ax.set_ylabel('b')
ax.plot(a_list, b_list, zs=cost_list, zdir='z', c='r', lw=3) # plot 3D gradient descent
plt.show()
更换INIT_PARAMS的值(更换中括号里的数字即可),可以看到不同的值,部分结果会收敛到局部最优解,部分结果会收敛到全局最优解。