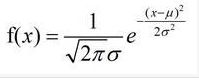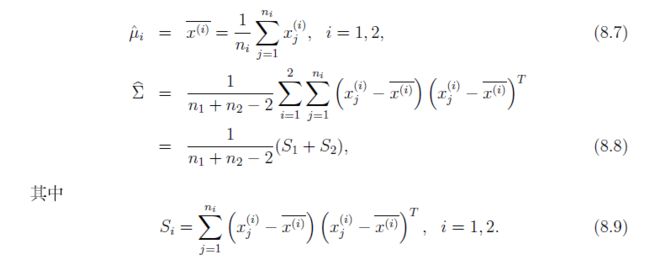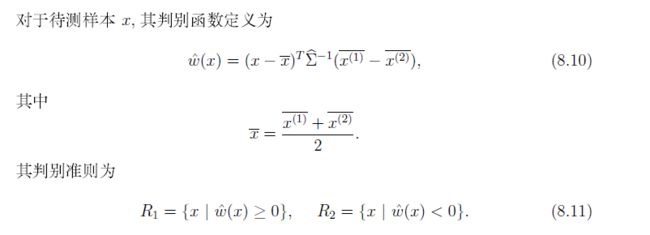距离判别法
距离判别法:距离判别方是通过计算待测点到各个分类的距离,在根据计算出距离的大小,进行判别该待测点属于那个分类。但是距离的计算是通过马氏距离进行计算的,而不是我们平常几何中用的欧式距离。
欧式距离的定义:
欧氏距离是最易于理解的一种距离计算方法,源自欧氏空间中两点间的距离公式。
(1)二维平面上两点a(x1,y1)与b(x2,y2)间的欧氏距离:
(2)三维空间两点a(x1,y1,z1)与b(x2,y2,z2)间的欧氏距离:
(3)两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的欧氏距离:
也可以用表示成向量运算的形式:
有M个样本向量X1~Xm,协方差矩阵记为S,均值记为向量μ,则其中样本向量X到u的马氏距离表示为:
而其中向量Xi与Xj之间的马氏距离定义为:
若协方差矩阵是单位矩阵(各个样本向量之间独立同分布),则公式就成了:
为什么使用马氏距离不使用欧式距离:
从上图两个分类服从正态分布u1和u2, u1 均值为0 方差为1
、
u2 均值为4 方差为2。A点在x轴的值为1.66
按照欧式距离进行计算A 点跟接近u1分类,他离u1 的平均值跟接近
按照马氏距离进行计算,我们对两个分类进行密度函数计算。
计算A属于u1分类概率密度=0.10
计算A
属于u2分类概率密度=0.33
上图也很好的解释为什么要考虑使用马氏距离,上图黄色椭圆部分代表整个分类在直角坐标系的排布情况,u代表分类的中心。图中有圆上有两个点分别是A和B ,使用欧式距离计算到u的距离是一样。但是从图中可以看出A点已经快出整个分类的范围,而B却在中心很密的位置。
距离判别法公式:
这里要讨论两种情况
情况1:分类来自一个总体,这样分类的协方差是一样的。
情况2:分类是来不同的总体,这样他们的协方差就不一样。
所以这里要考虑协方差相同的情况和不相同的情况
公式推理:
设总体x1 和x2,他们的均值分别是u1和u2,协方差分别是
Σ1和Σ2.
x 为待测样本
情况1,协方差相同
μ1
≠
μ2, Σ1 = Σ2 = Σ
均值和协方差计算
化简得
R 实现代码
#TrnX1类别1 TrnX2类别2 TstX测试集 var.equal方差是否一样
discriminiant.distance <- function(TrnX1, TrnX2, TstX = NULL, var.equal = FALSE){
if (is.null(TstX) == TRUE) TstX <- rbind(TrnX1,TrnX2)
if (is.vector(TstX) == TRUE) TstX <- t(as.matrix(TstX))
else if (is.matrix(TstX) != TRUE)
TstX <- as.matrix(TstX)
if (is.matrix(TrnX1) != TRUE) TrnX1 <- as.matrix(TrnX1)
if (is.matrix(TrnX2) != TRUE) TrnX2 <- as.matrix(TrnX2)
nx <- nrow(TstX)
blong <- matrix(rep(0, nx), nrow=1, byrow=TRUE,
dimnames=list("blong", 1:nx))
mu1 <- colMeans(TrnX1); mu2 <- colMeans(TrnX2)
if (var.equal == TRUE || var.equal == T){
S <- var(rbind(TrnX1,TrnX2))
w <- mahalanobis(TstX, mu2, S)
- mahalanobis(TstX, mu1, S)
}
else{
S1 < -var(TrnX1); S2 <- var(TrnX2)
w <- mahalanobis(TstX, mu2, S2)
- mahalanobis(TstX, mu1, S1)
}
for (i in 1:nx){
if (w[i] > 0)
blong[i] <- 1
else
blong[i] <- 2
}
blong
}
classX1<-data.frame(
x1=c(6.60, 6.60, 6.10, 6.10, 8.40, 7.2, 8.40, 7.50,7.50, 8.30, 7.80, 7.80),
x2=c(39.00,39.00, 47.00, 47.00, 32.00, 6.0, 113.00, 52.00,52.00,113.00,172.00,172.00),
x3=c(1.00, 1.00, 1.00, 1.00, 2.00, 1.0, 3.50, 1.00,3.50, 0.00, 1.00, 1.50),
x4=c(6.00, 6.00, 6.00, 6.00, 7.50, 7.0, 6.00, 6.00,7.50, 7.50, 3.50, 3.00),
x5=c(6.00, 12.00, 6.00, 12.00, 19.00, 28.0, 18.00, 12.00,6.00, 35.00, 14.00, 15.00),
x6=c(0.12, 0.12, 0.08, 0.08, 0.35, 0.3, 0.15, 0.16,0.16, 0.12, 0.21, 0.21),
x7=c(20.00,20.00, 12.00, 12.00, 75.00, 30.0, 75.00, 40.00,40.00,180.00, 45.00, 45.00)
)
classX2<-data.frame(
x1=c(8.40, 8.40, 8.40, 6.3, 7.00, 7.00, 7.00, 8.30,8.30, 7.2, 7.2, 7.2, 5.50, 8.40, 8.40, 7.50,7.50, 8.30, 8.30, 8.30, 8.30, 7.80, 7.80),
x2=c(32.0 ,32.00, 32.00, 11.0, 8.00, 8.00, 8.00,161.00,161.0, 6.0, 6.0, 6.0, 6.00,113.00,113.00, 52.00,52.00, 97.00, 97.00,89.00,56.00,172.00,283.00),
x3=c(1.00, 2.00, 2.50, 4.5, 4.50, 6.00, 1.50, 1.50,0.50, 3.5, 1.0, 1.0, 2.50, 3.50, 3.50, 1.00,1.00, 0.00, 2.50, 0.00, 1.50, 1.00, 1.00),
x4=c(5.00, 9.00, 4.00, 7.5, 4.50, 7.50, 6.00, 4.00,2.50, 4.0, 3.0, 6.0, 3.00, 4.50, 4.50, 6.00,7.50, 6.00, 6.00, 6.00, 6.00, 3.50, 4.50),
x5=c(4.00, 10.00, 10.00, 3.0, 9.00, 4.00, 1.00, 4.00,1.00, 12.0, 3.0, 5.0, 7.00, 6.00, 8.00, 6.00,8.00, 5.00, 5.00,10.00,13.00, 6.00, 6.00),
x6=c(0.35, 0.35, 0.35, 0.2, 0.25, 0.25, 0.25, 0.08,0.08, 0.30, 0.3, 0.3, 0.18, 0.15, 0.15, 0.16,0.16, 0.15, 0.15, 0.16, 0.25, 0.21, 0.18),
x7=c(75.00,75.00, 75.00, 15.0,30.00, 30.00, 30.00, 70.00,70.00, 30.0, 30.0, 30.0,18.00, 75.00, 75.00, 40.00,40.00,180.00,180.00,180.00,180.00,45.00,45.00)
)
discriminiant.distance(classX1, classX2, var.equal=TRUE)
discriminiant.distance(classX1, classX2)
上述函数方法是解决两个分类的情况。如果出现多分类情况,可以通过分类的距离进行排序,取距离最近一个分类,即为当前待测变量的分类。
实现代码如下:
distinguish.distance <- function(TrnX, TrnG, TstX = NULL, var.equal = FALSE){
if ( is.factor(TrnG) == FALSE){
mx <- nrow(TrnX); mg <- nrow(TrnG)
TrnX <- rbind(TrnX, TrnG)
TrnG <- factor(rep(1:2, c(mx, mg)))
}
if (is.null(TstX) == TRUE) TstX <- TrnX
if (is.vector(TstX) == TRUE) TstX <- t(as.matrix(TstX))
else if (is.matrix(TstX) != TRUE)
TstX <- as.matrix(TstX)
if (is.matrix(TrnX) != TRUE) TrnX <- as.matrix(TrnX)
nx <- nrow(TstX)
blong <- matrix(rep(0, nx), nrow=1,
dimnames=list("blong", 1:nx))
g <- length(levels(TrnG))
mu <- matrix(0, nrow=g, ncol=ncol(TrnX))
for (i in 1:g)
mu[i,] <- colMeans(TrnX[TrnG==i,])
D < -matrix(0, nrow=g, ncol=nx)
if (var.equal == TRUE || var.equal == T){
for (i in 1:g)
D[i,] <- mahalanobis(TstX, mu[i,], var(TrnX))
}
else{
for (i in 1:g)
D[i,] <- mahalanobis(TstX, mu[i,], var(TrnX[TrnG==i,]))
}
for (j in 1:nx){
dmin <- Inf
for (i in 1:g)
if (D[i,j] < dmin){
dmin <- D[i,j]; blong[j] <- i
}
}
blong
}