HaffManTree哈夫曼树的编码和解码的个人学习心得感悟
曾经HaffManTree的编码和解码对我来实在是头疼,一谈论关于哈夫曼树的编码和解码我就分分钟钟想打人,原因无他,看不懂HaffManTree的构建方式;看懂了HaffManTree的构建方式,但是编码用计算机语言来实现太麻烦,逻辑上好绕。
曾经再网上查阅的大部分的关于HaffManTree树的文章,讲的都很理论,逻辑复杂,难以读懂(逻辑复杂可能是数据结构导致的错)。
今天,我终于找到一个很好的方式,一种很好的数据结构来完美进行HaffManTree的构建和编码和解码。下面笔者将详细介绍这个过程,不仅仅是为了读者能看懂,同时也是为了增加笔者对HaffManTree树的更深层次的理解和感悟,顺便做下笔记,等以后再来看看或者出本书也是一个不错的选择。
百度百科对HaffManTree算法是这样解释的:
哈夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树。所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为0层,
叶结点到根结点的路径长度为叶结点的层数)。树的带权路径长度记为WPL=(W1L1+W2L2+W3L3+…+ WnLn),N个权值Wi(i=1,2,…n)构成一棵有N个叶结点的二叉树,
相应的叶结点的路径长度为Li(i=1,2,…n)。可以证明哈夫曼树的WPL是最小的。
构造哈夫曼树的算法如下:
1)对给定的n个权值{W1,W2,W3,…,Wi,…,Wn}构成n棵二叉树的初始集合F={T1,T2,T3,…,Ti,…, Tn},其中每棵二叉树Ti中只有一个权值为Wi的根结点,它的左右子树均为空。
2)在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树,新二叉树的根结点的权值为其左右子树的根结点的权值之和。
3)从F中删除这两棵树,并把这棵新的二叉树同样以升序排列加入到集合F中。
4)重复2)和3),直到集合F中只有一棵二叉树为止。
在百度百科对HaffManTree介绍的页面上面还附带了各种语言实现的HaffManTree的构建,编码和解码代码,读者可以先去看下,可能会一头雾水,也有可能是云里雾里,也可能一下子就看懂。
由于笔者最先接触HaffManTree是从 李春葆_数据结构(第四版)一书中获知,所以最先解释下次数HaffManTree的构建和编码
(这一段是该书的内容)
为了实现构造哈夫曼树的算法,设计哈夫曼树中每个结点类型如下:
typedef struct
{ char data; /*结点值*/
float weight; /*权重*/
int parent; /*双亲结点*/
int lchild; /*左孩子结点*/
int rchild; /*右孩子结点*/
} HTNode;
用ht[]数组存放哈夫曼树,对于具有n个叶子结点的哈夫曼树,总共有2n-1个结点。
其算法思路是:
n个叶子结点只有data和weight域值,先将所有2n-1个结点的parent、lchild和rchild域置为初值-1。处理每个非叶子结点ht[i](存放在ht[n]~ht[2n-2]中):从ht[0] ~ht[i-2]中找出根结点(即其parent域为-1)最小的两个结点ht[lnode]和ht[rnode],将它们作为ht[i]的左右子树,ht[lnode]和ht[rnode]的双亲结点置为ht[i],并且ht[i].weight=ht[lnode].weight+ht[rnode].weight。如此这样直到所有2n-1个非叶子结点处理完毕。
构造哈夫曼树的算法如下:
void CreateHT(HTNode ht[],int n)
{ int i,j,k,lnode,rnode; float min1,min2;
for (i=0;i<2*n-1;i++) /*所有结点的相关域置初值-1*/
ht[i].parent=ht[i].lchild=ht[i].rchild=-1;
for (i=n;i<2*n-1;i++) /*构造哈夫曼树*/
{ min1=min2=32767; lnode=rnode=-1;
for (k=0;k<=i-1;k++)
if (ht[k].parent==-1)/*未构造二叉树的结点中查找*/
{ if (ht[k].weight哈夫曼编码
具体构造方法如下:设需要编码的字符集合为{d1,d2,…,dn},各个字符在电文中出现的次数集合为{w1,w2,…,wn},以d1,d2,…,dn作为叶结点,以w1,w2,…,wn作为各根结点到每
个叶结点的权值构造一棵二叉树,规定哈夫曼树中的左分支为0,右分支为1,则从根结点到每个叶结点所经过的分支对应的0和1组成的序列便为该结点对应字符的编码。这样的编码
称为哈夫曼编码。
为了实现构造哈夫曼编码的算法,设计存放每个结点哈夫曼编码的类型如下:
typedef struct
{
char cd[N]; /*存放当前结点的哈夫曼码*/
int start; /*存放哈夫曼码在cd中的起始位置*/
} HCode;
根据哈夫曼树求对应的哈夫曼编码的算法如下:
void CreateHCode(HTNode ht[],HCode hcd[],int n)
{ int i,f,c; HCode hc;
for (i=0;i现在读者两评价一下这两段代码在该书中出现的好坏,该书前面提到的构建书都是返回一个节点指针(或者不返回数据,直接获取节点指针的引用),这里的函数突然要求你传入一个数组,突入起来的一招,让我防不胜防,一个大写的尴尬。也就意味着代码的大改动,这是比较耗费时间和精力的而且还增加了一些难度(针对个人能力而言)。
反正读者当时读这本书的上述的代码及算法思路,还是读了多变才读懂的,只能归根于这个算法不是很适合首次接触哈夫曼树的初学者。下面进入今天的正题,说说读者给出的代码和此书给出的代码,读者的逻辑和此书的逻辑。
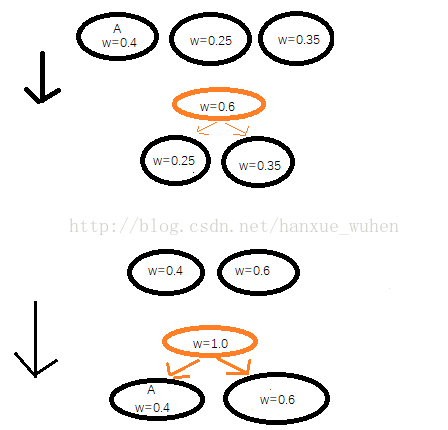
1:首先我们看下图(使用优先队列巧妙构造哈夫曼树)
通过上面的三张图可以看出我们构造哈夫曼树的一个过程,即从所有节点李米娜找到权重最小和权重次小的节点权重相加构造新节点,新节点代替原有两个节点参加和剩余节点参加下一轮构造。此时我自然而然的想到了优先队列(PriorityQueue)(百度百科),这个数据结构能解决掉我们两个较小节点相加的问题。
2:哈夫曼树编码(这里采用两种方法:递归先序遍历哈夫曼树+编码 非递归先序遍历哈夫曼树+编码(使用栈这个数据结构))
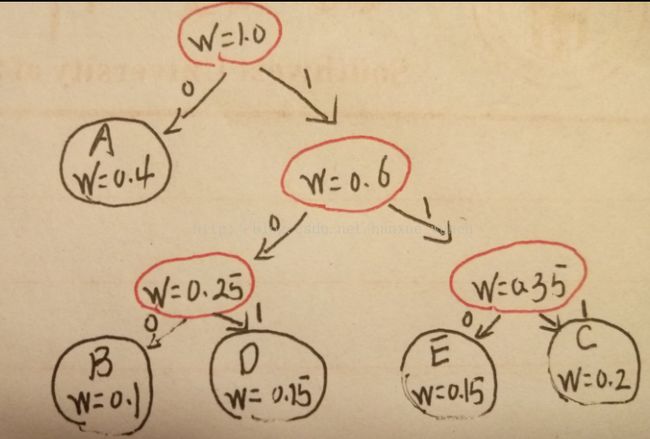
在上代码之前,笔者先给读者做个铺垫:通过上图可以看到 w=0.25的哈夫曼编码序列是10,B(w=0.1)的哈夫曼编码序列是100,D(w=0.15)的哈夫曼编码序列是101
请读者仔细观察这三者的关系:
B的哈夫曼编码序列= (w=0.25)的哈夫曼编码序列 + 0 ,即 100 = 10 + 0 = 100
C的哈夫曼编码序列= (w=0.25)的哈夫曼编码序列 + 1 ,即 101 = 10 + 1 = 101
这里对应笔者最终代码的这几句代码:
node.codeString.append(node.parent.codeString+"0");
node.codeString.append(node.parent.codeString+"1");
p.codeString.append(p.parent != null ? p.parent.codeString:"" +"1");
p.codeString.append(p.parent != null ? p.parent.codeString:"" +"0");现在上最终代码吧
import java.util.Scanner;
public class HaffManTree {
static int MaxSize = 0 ;
public static void main(String[] args) {
System.out.println("请输入哈夫曼编码节点个数");
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
MaxSize = n ;
PriorityQueue priorityQueue = new PriorityQueue(n+1);
//A 0.4 B 0.1 C 0.2 D 0.15 - 0.15
//A 0.35 B 0.1 C 0.2 D 0.2 E 0.15
//Ctrl+Z结束输入:scanner.hasNext(),但是反应十分慢
//a 1 b 2 c 1.5 S 2 Y 10 f 11 A 0.35 B 0.1 C 0.2 - 20
System.out.println("请输入哈夫曼树节点的信息,例如:(节点符号值{符号不能包含'$'} 节点权值):A 0.2 ,按enter输入·下一节点信息");
while(n>0)
{
Node node = new Node();
node.data = scanner.next().charAt(0);
node.probability = scanner.nextDouble();
priorityQueue.insert(node);
n--;
}
Node item_left=null ,item_right=null ,item_parent=null ;
while(!priorityQueue.isEmpty() )
{
//左节点"0",右节点"1" ;
item_left = priorityQueue.remove();
item_right = priorityQueue.remove();
if(item_right != null){
Node node = new Node();
node.probability = item_left.probability+item_right.probability;
node.leftChild = item_left ;
node.rightChild = item_right ;
item_left.parent = node ;
item_right.parent = node ;
node.data='$';
priorityQueue.insert(node);
node = null ;
}else{
item_parent=item_left ;
}
}
//此处必须传入0:表示最原始树的根节点root
PreOrder(item_parent,0);
System.out.println();
PreOrder_1(item_parent);
}
//在遍历中进行编码
//先序递归遍历 node和进行哈夫曼编码:跟节点
//flag: 1:当前访问的是左节点 2:当前访问的是右节点 ,默认传入0:表示最原始树的根节点root
//left:左节点"0", right:右节点"1" ;
public static void PreOrder(Node node ,int flag)
{
if(node != null)
{
if(flag == 1){
node.codeString.append(node.parent.codeString+"0");
}
if(flag == 2){
node.codeString.append(node.parent.codeString+"1");
}
//输出haffManTree树的原始节点
if(node.data != '$')
System.out.println(Node.toString(node));
PreOrder(node.leftChild,1);
PreOrder(node.rightChild,2);
}
}
//在遍历中进行编码
//先序非递归遍历和进行哈夫曼编码
public static void PreOrder_1(Node node){
Node[] St = new Node[MaxSize];
int top = -1 ;
Node p ;
if(node != null)
{
top++;
St[top] = node ;
while(top > -1)
{
p=St[top];
top--;
if(p.data != '$')
System.out.println(Node.toString(p));
if(p.rightChild != null)
{
p.codeString.append(p.parent != null ? p.parent.codeString:"" +"1");
top++;
St[top] = p.rightChild;
}
if(p.leftChild != null)
{
p.codeString.append(p.parent != null ? p.parent.codeString:"" +"0");
top++;
St[top]=p.leftChild;
}
}
System.out.println();
}
}
}
//哈夫曼树节点
class Node
{
Node parent = null ;
Node leftChild = null ;
Node rightChild = null ;
char data ; //节点符号
double probability ; // 概率 weight:权值
StringBuffer codeString = new StringBuffer() ; //编码序列
public static String toString(Node item)
{
return "[data:"+item.data +",codeString:"+item.codeString.toString()+",probability:"+item.probability+"]" ;
}
}
//优先队列
class PriorityQueue
{
private int maxSize ;
private Node[] queueArray ;
private int mItems ;
public PriorityQueue(int s)
{
maxSize = s ;
queueArray = new Node[maxSize];
mItems = 0 ;
}
//优先队列插入元素
public void insert(Node item)
{
int j ;
if(mItems == 0)
{
queueArray[mItems++] = item ;
}
else
{
for(j=mItems-1 ;j>=0 ;j--)
{
//为了保证输出的是HaffManTree带全路径长度最短,
//故item.probability >= queueArray[j].probability
//而不能只是item.probability > queueArray[j].probability
//因为新构造的节点的权值假如和已有节点权值相等,为了避免新节点比已有权值相等的节点
//新参与构造,导致带全路径增加,故把新构造的节点总是尽可能放在优先队列的最底层
if(item.probability > queueArray[j].probability)
queueArray[j+1] = queueArray[j];
else
break ;
}
queueArray[j+1]=item;
mItems++;
}
}
//移除优先队列最顶层元素
public Node remove()
{
return mItems >= 1 ? queueArray[--mItems] : null;
}
//查找优先队列最顶层一个元素
public Node peekMin()
{
return queueArray[mItems-1];
}
//判断优先队列是否为空
public boolean isEmpty()
{
return (mItems==0) ;
}
//判断优先队列是否满了
public boolean isFull()
{
return (mItems==maxSize);
}
//获取优先队列的大小
public int size()
{
return mItems ;
}
}程序运行截图:
笔者在最终代码中用了先序递归遍历二叉树和先序非递归编历二叉树进行编码(非递归中使用的栈这种数据结构),我们都知道,递归遍历二叉树非常消耗内存,当节点数量很多时,不可避免的出现堆栈溢出的异常,而使用非递归编码二叉树,虽然逻辑可能会有点绕,但会避免堆栈溢出的问题。
其实先序使用栈进行先序非递归遍历二叉树的逻辑也比较好理解:
先序遍历二叉树顺序: 根节点------左子树--------右子树
1:根节点进栈,根节点出栈,根节点的右子节点进栈,根节点的左子节点进栈
2:根节点的左子节点A出栈,A右子节点进栈,A的左子节进栈(当栈不为空时一直重复2的操作)
这时我们的出栈的顺序那就肯定为: 根节点,左子树,右子树 (左子树又有跟节点,左子树,右子树 ;右子树又有跟节点,左子树,右子树)
解码以后在写了