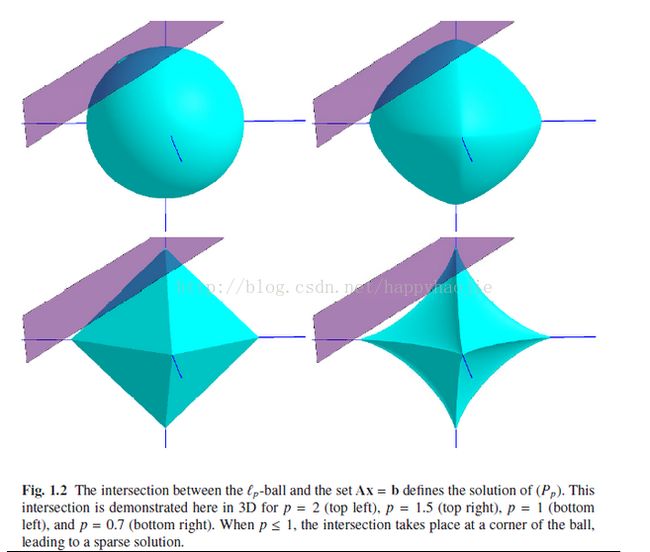
【Compressive Sensing】压缩感知初体验

压缩感知是由E. J. Candes、J. Romberg、T. Tao 和D. L. Donoho于2004年提出来的，但在此前已经出现了雏形，这个不深究。

陶哲轩曾经写过一篇关于压缩感知的科普文章《压缩感知和单像素相机》，最顶尖的科学奖写科普文章很难得，当然有必要学习。虽然这篇文章直言是为非数学专业的人写的，但是理解起来依然非常困难，因为涉及的数学知识非常多，下面我们一起来学习这篇文章，因为本人是初学者，还有很多问题没搞明白，请多多指教。

1、文章中有这句话：两百万个像素用8位灰度值就是2MB，16位灰度就是4MB。

理解：因为这里指的是灰度图像，而不是非黑即白的二值图像，所以如果用8位表示的话，在不压缩的情况下一个像素需要8bit（1字节，256种状态），而如果用16位表示的话，在不压缩的情况下一个像素需要16bit（2字节，65536种状态）。

2、不太高级的压缩技术引出的问题。

理解：对于给定的一张图片，我们可以选取可见色块中色差较小的某块，记录该块的维度、坐标和颜色，剩下微小的残余误差。然后继续搜索剩余的色块，直到整张图片只剩下色彩强度很小，肉眼无法察觉的细节。反向操作就可以还原出比原始图片质量低的重建图片，但是占用空间却小很多。

以上算法不适用于颜色剧烈变化的情况，实际应用不是很有效，因为颜色剧烈变化就没办法用平均色块来表示，而应该用“不均匀色块”表示：如果右半边色彩强度平均值大于左半边这样的色块。这种情况可以用二维Haar小波系统来描述，或者用人们后来发现的一种更平滑的小波系统避免误差，这是由小波的特性决定的（如果不太懂的，可以先去看一下小波相关的知识，定性理解一下），总之基本原理就是：把原始图像表示为不同“小波（类似于上文中的色块）”的线性叠加，记录显著的（高强度的）小波的系数，放弃掉（或者用阈值排除掉）剩下的小波系数。

JPEG 2000用的就是离散小波变换（DWT），但是比这种“小波系数阈值法”要精细很多。

而一张1024*2048的图像可能会有200百万自由度，因此需要200多万个不同的小波来描述，才可能完美重建，而从小波的角度来说，这些小波系数是稀疏的，只有一部分是重要的，另一部分提供极少有用的信息，可以舍弃掉，比如说200多万个小波系数只有10万是重要的，我们只需要记录这10万个就够了。

可是，我们并不知道哪10万个是重要的，所以不得不对200多万个小波系数一一计量，找出重要的10万个，这就需要200多万次，非常可怕。如果随机选取了10万个系数，但这10万个系数并不是最重要的，相当于把图片中有用的信息丢掉了，这反而弄巧成拙了。

解决办法：就是用非小波的算法来做30万个测量——尽管我前面确实讲过小波算法是观察和压缩图像的最佳手段。实际上最好的测量其实应该是（伪）随机测量——比如说随机生成30万个“滤镜”图像并测量真实图像与每个滤镜的相关程度。这样，图像与滤镜之间的这些测量结果（也就是“相关性”）很有可能是非常小非常随机的。但是——这是关键所在——构成图像的2百万种可能的小波函数会在这些随机的滤镜的测量下生成自己特有的“特征”，它们每一个都会与某一些滤镜成正相关，与另一些滤镜成负相关，但是与更多的滤镜不相关。可是（在极大的概率下）2百万个特征都各不相同；更有甚者，其中任意十万个的线性组合仍然是各不相同的（以线性代数的观点来看，这是因为一个30万维线性子空间中任意两个10万维的子空间极有可能互不相交）。因此，基本上是有可能从这30万个随机数据中恢复图像的（至少是恢复图像中的10万个主要细节）。简而言之，我们是在讨论一个哈希函数的线性代数版本。

意思如下：可以随机生成30万个滤镜图像，应该是指30万个元素，原图是200多万个元素，因为是随机生成的，所以滤镜和原图之间非相关性大，滤镜和原图得到的是30万个随机数据，这30万个随机数据包含了原图的信息，而且达到了降维的效果，这其实就是随机测量矩阵的作用，我们需要做的就是找到一个合适的观测矩阵，然后从30万个观测数据中恢复原始图像。30万个线性组合不相关表示30万个方程至少可以解出30万个未知数，而30万线性子空间任意两个10万维子空间不相交那就说明至少可以解出10万个未知数，这样就表示至少可以恢复出图像中的10万个重要细节。

如果知道200万个系数中哪10万个是重要的，就可以利用标准的线性代数来重建图像。事实上我们并不能提前知道哪些系数是重要的，这又如何还原图像呢？可以用最小二乘近似法得出全部200万个系数，进而得出200万个像素重建图像，但还原出的图像会含有大量颗粒噪声，并不可取。可以为每一组可能的10万关键系数都做一次线性代数处理，但是这样做的耗时非常恐怖，我认为是C(200万，10万)，陶哲轩说大约是10的17万次方个组合，不可行。

陶哲轩给出了两种可行的恢复原图像的方法：

NO.1、匹配追踪法(MP):找到一个其标记看上去与收集到的数据相关的小波；在数据中去除这个标记的所有印迹；不断重复直到我们能用小波标记“解释”收集到的所有数据。

看起来并不好懂，那就分步骤解释吧：

1)从字典矩阵D（过完备原子库）中选择一个与原始信号y最匹配的原子（字典矩阵D中的某列），方法就是：计算信号 y 与字典矩阵中每列(原子)的内积，选择绝对值最大的一个原子，它就是与信号 y 在本次迭代运算中最匹配的原子。

用专业术语说：令信号，从字典矩阵中选择一个最为匹配的原子，满足，r0 表示一个字典矩阵的列索引。这样，信号 y 就被分解为在最匹配原子的垂直投影分量和残值两部分，即：。

2)对残值R1f按照上面的步骤进行同样的分解，那么第K步可以得到：

， 其中 满足。

可见，经过K步分解后，信号 y 被分解为：，其中。

需要说明的是：MP算法是收敛的，因为，和正交，由这两个可以得出，得出每一个残值比上一次的小，故而收敛。

（上面的公式有些错误，我不知道csdn博客怎么插入公式，不过大家应该很容易看出来，懂得原理就成了）

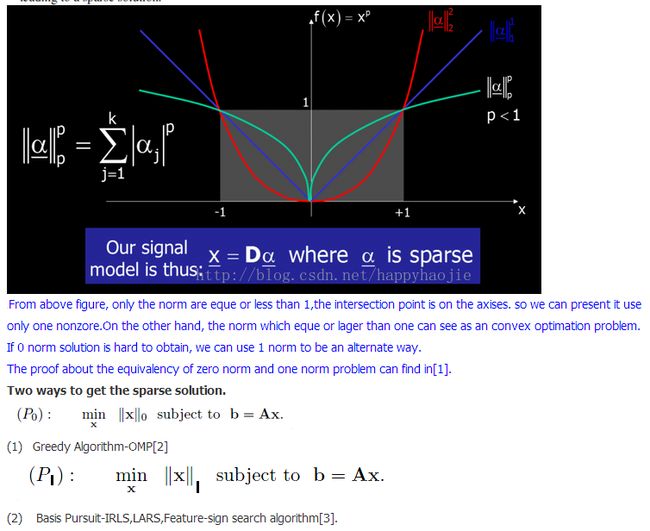
NO.2、 基追踪（又名L1模最小化）：在所有与录得数据匹配的小波组合中，找到一个“最稀疏的”，也就是其中所有系数的绝对值总和越小越好。（这种最小化的结果趋向于迫使绝大多数系数都消失了。）这种最小化算法可以利用单纯形法之类的凸规划算法，在合理的时间内计算出来。

听起来也不好懂，简单来说就是：把0范数问题转化为1范数问题，因为0范数表示的是向量中非零元素的个数，是NP问题，无法求解，可以等价转化为1范数凸优化问题，1范数的意思就是绝对值之和，因为稀疏，在这里当然是绝对值总和越小越好。（以后还会具体提到该算法，下面贴一下甄亮利老师一篇博文的精华部分，便于理解）

这篇文章的权威性是毋庸置疑的，但前面说了理解起来并不简单，因此本人也有些疑惑的地方。

1、传统相机会测量每一个像素的亮度（在上述例子中就是二百万个测量值），结果得到的图片文件就比较大（用8位灰度值就是2MB，16位灰度就是4MB）。数学上就认为这个文件是用超高维矢量值描绘的（在本例中就是约二百万维）。

疑惑：“超高维矢量值”，“约二百万维”这个是怎么得来的？应该怎么计算维度？因为一般说，一张图无论像素多少个，我们都认为它是二维的。

2、关键是尽管“所有图片”所构成的空间要占用2MB的“自由度”或者说“熵”。

疑惑：为什么说是“自由度”和“熵”？自由度还勉强可以理解，但是说是“熵”我就理解不了了。如果定性不定量理解的话，熵表示的是混乱的程度，某种意义上的自由度。

3、在图像上设置一种合适的“过滤器”或叫“滤镜”，然后计量过滤出来的每个像素的色彩强度，是一种可行的系数计量方法。

疑惑：不太懂这个计量方法，这里说得好像是把色彩强度大的像素过滤出来。

参考文献：

1、匹配追踪算法基本概念介绍

http://blog.sina.com.cn/s/blog_5156997b0101qu5f.html

2、An introduction to Sparse Representation

http://blog.sciencenet.cn/home.php?mod=space&uid=621576&do=blog&id=551052